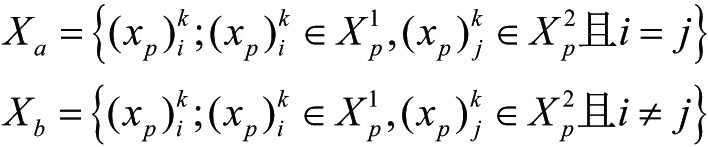JAIT

I.INTRODUCTION

Personal identity identification has important applications in social welfare security, financial markets, national security, e-government, and other fields. Uniqueness is the key to personal identity. Traditional personal identity authentication methods cannot effectively distinguish the owner of identity markers and the impostor who obtains the markers. With the emergence of biometric technology, this problem has been solved to a large extent. Human ear image recognition is a new biometric recognition technology emerging in recent years, which extracts the features of human ear by computer and authenticates the identity according to these features [1,2]. The human ear is as innate as any other biological feature of the human body, such as fingerprints, or faces, and its unique features provide a necessary prerequisite for identity identification. Scholars have conducted some preliminary research on human ear recognition, for example, Youbi et al. developed a new framework to ear recognition in light of the local binary pattern descriptor by partitioning the image into several equal parts [3]. Guermoui et al. presented a two-stage ear in recognition framework by combining sparse representation with the local descriptor [4]. Rahhal et al. exploited a novel descriptor of intensive local phase quantization for ear recognition by making use of the phase responses [5]. Tré et al. investigated an effective bipolar measure for calculating the similarity among multiple features which can be applied for 3D ear image recognition process [6]. Prakash et al. proposed an ear recognition technique which takes advantage of 3D assisted with co-registered 2D ear images [7]. Compared with other biometric recognition technologies [8,9], human ear has the advantages of stable and rich structure, not affected by facial expression and makeup, easier to collect, more acceptable, and not easy to deceive. Therefore, human ear recognition is becoming another hot spot in the field of biometric recognition, and ear recognition is expected to become a new biometric recognition technology, which is as important as face recognition, iris recognition, and fingerprint recognition and can be complemented and combined with each other. Plenty of insightful findings related to human ear recognition have been proposed, which are beneficial for identification. For example, Hasan et al. exploited human identification technique which makes use of the depth representation created by residual networks and spatial coding blocks through human ear images [10]. Sinha et al. investigated the identity authentication technique which takes advantage of histogram of oriented gradients and support vector machine (SVM) to locate ears and further uses convolutional neural networks to identify ear images for authentication [11]. Kumar et al. presented a human identification method which makes use of the robust segmentation for curved area of interest based on Fourier descriptors and morphological operators [12].

Feature extraction is one of the key links of pattern recognition technology [13 –15]. At present, the common methods of feature extraction in human ear recognition include principal component analysis (PCA) [16 –18], independent component analysis (ICA) [19 –21], two-dimensional principal component analysis (2DPCA) [22,23], Fisherface [24 –26], and Fisher linear discriminant [27,28]. However, these methods of single feature extraction can only get a high recognition rate under certain circumstances. Otherwise the recognition effect is not good. Hence, the method of complementary double feature is a way to improve the recognition rate. How to improve recognition effect has become a burning and challenging issue. Therefore, in this study, the method of PCA combined with Fisherface is proposed to overcome the disadvantages of PCA and single feature extraction of Fisher linear discriminant. In a feature subspace, the patterns can be separated as two parts. One part is easy to recognize while the other part is difficult to recognize. Then the difficult patterns can be projected to another feature subspace for recognition. Therefore, it is necessary to find two feature subspaces with certain complementarity. In the latter subspace, it is possible to make a correct classification of the pattern that is difficult to identify in the former subspace. The idea of complementary double feature extraction proposed in this paper comes from this.

In this paper, it is necessary to divide the pattern into two parts, which need to be completed by the pre-classification of two different classifiers, respectively. Furthermore, one part is easier to recognize, and the other counterpart is more difficult to recognize in a feature subspace. In addition, the extraction of complementary double features needs to be done in two different subspaces. Therefore, the selection of the two subspaces should comprehensively consider their classification capabilities and complementarities. In this paper, the extraction of double features is carried out in the dual space. The dual space is composed of principal component analysis algorithm and Fisherface algorithm. PCA is the optimal representation of pattern samples in the sense of minimum covariance. Since PCA only considers second-order statistical information, its effect is to remove the correlation between image components. By choosing Fisherface as complementary space, we use the best discriminant information of patterns as the complementary information of optimal representation. Therefore, PCA and Fisherface form complementary double space, which is suitable for the proposed complementary double feature extraction method. On the one hand, this method improves the performance of human ear recognition, on the other hand, it makes up for the shortcomings of single feature extraction, such as reducing the sensitivity to noise and light conditions, and provides a practical method for human ear recognition.

The major contributions of this study are as follows: (1) As a biological feature of individual recognition, human ear mainly contains some important conditions such as universality, collectability, non-disturbance, stability, and uniqueness, improving the rate of human ear recognition is the focus of the research. (2) PCA, ICA and other single feature extraction methods have limitations in recognition rate, in this paper, the method of PCA combined with Fisherface is proposed to overcome the disadvantages of single feature extraction, the main idea is that the patterns can be separated as two parts in a subspaces, one part is easy to recognize while the other part is difficult to recognize. Then the difficult patterns can be projected to another feature subspace for recognition. (3) The algorithm has been tested on the human ear image library provided by University of Science and Technology Beijing, and the data obtained show a high recognition rate, which has a high application value.

II.PRINCIPAL COMPONENT ANALYSIS

A.THE DEFINITION OF PCA

PCA method is a statistical method based on K-L transform. The main idea is to extract the main features of the space raw data, reduce data redundancy, the features of the data in a lower dimensional space is processed, while maintaining the most useful information of the original data, also to solve the bottleneck problem of high dimension of data space. In recent years, PCA has been widely used in signal processing, pattern recognition, biometric recognition and other fields [29,30].

B.PCA METHOD BASED ON K-L TRANSFORM

K-L transform [31,32] is a kind of optimal orthogonal transformation of image compression. The essence of K-L is to establish a new coordinate system and align the main axis of an object along the feature vector for rotation transformation. This transformation removes the correlation between components of the original data vector, and it is possible to remove those coordinate systems with less information to reduce the dimension of feature space. It has been applied to feature extraction, which aims to describe the sample with a small number of features while retaining the required identification information.

The principle of PCA is as follows:

Given that the random vector of n-dimensional space is expressed by $ϕ (ϕ \in R^{n})$ , the formula is used to zero $ϕ$ , $x = ϕ - E (ϕ)$ , then $E (ϕ) = 0$ , if x is expanded by a set of complete orthogonal basis $u_{j}$ , $j = 1, 2, \dots \dots N$ , the formula can be expressed as follows:

x = \sum_{j = 1}^{N} α_{j} u_{j}

(1)

Assuming that only the first K items are used for reconstruction, the formula can be obtained as follows:

x_{rec} = \sum_{j = 1}^{k} α_{j} u_{j}

(2)

The mean squared error formula of $x_{rec}$ can be described as follows:

ɛ = E [{(x - x_{rec})}^{T} (x - x_{rec})]

(3)

The properties of a complete orthogonal basis are expressed as follows:

{u_{i}}^{T} u_{j} = {\begin{cases} 1, & j = i \\ 0, & j \neq i \end{cases}

(4)

In addition, equation (5) can be obtained as follows after transforming equation (1):

a_{j} = {u_{j}}^{T} x

(5)

The mean squared error formula is transformed as follows:

ɛ = E [\sum_{j = k + 1}^{n} u_{j} x x^{T} u_{j}] = \sum_{j = k = 1}^{n} {u_{j}}^{T} c u_{j}

(6)

c

in equation (6) is the total covariance of

x

and

ϕ

, the formula of

c

is as follows:

c = E [x x^{T}] = E [(ϕ - E [ϕ]) {(ϕ - E [ϕ])}^{T}]

(7)

In order to minimize the mean squared error of reconstruction and to better meet the constraints of orthogonality conditions, the Lagrange multiplier method is used to take the derivative of the function formula (8) from $u_{j}$ $(j = k + 1, \dots \dots N)$ to obtain formula (9).

J (u_{j}) = \sum_{j = k + 1}^{n} {u_{j}}^{T} c u_{j} - \sum_{j = k + 1}^{n} λ_{j} ({u_{j}}^{T} u_{j} - 1)

(8)

(c - λ_{j} I) u_{j} = 0 j = k + 1, \dots \dots N

(9)

Set the value of $k$ in equation (9) to $k = 1$ , $U_{1}, U_{2}, \dots \dots, U_{N}$ are the eigenvectors of the total covariance matrix $c$ , $λ_{1}, λ_{2}, \dots, λ_{n}$ are the eigenvalues of the total covariance matrix $c$ respectively. The space spanned by the orthogonalization of these eigenvectors is called the eigenspace. When the eigenvectors $U_{1}, U_{2}, \dots, U_{N}$ are arranged in descending order according to the eigenvalues, the conclusion of the eigenvalues is: $λ_{1} \geq λ_{2} \geq \dots \geq λ_{n}$ . At the same time, the following conclusions can be obtained:

For any random variable $X$ , if the eigenvectors corresponding to the first $K$ largest non-zero eigenvalues of the total covariance matrix $C$ are used as the coordinate axis to expand, the minimum truncated mean square error $ɛ_{\min}$ of all orthogonal expansions can be obtained under the same truncation length. The minimum truncated mean square error $x_{rec}$ is shown in formula (10).

ɛ_{\min} = \sum_{j = k + 1}^{n} λ_{j}

(10)

In equation (10), the selection rule of $k$ is that the ratio of the sum of the eigenvalues corresponding to the reserved eigenvectors to the sum of the total eigenvalues is greater than a certain threshold value $e$ . The value of $e$ is usually taken as 0.95, the value of $k$ can be calculated according to equation (11).

e = \sum_{i = 1}^{k} λ_{i} / \sum_{j = 1}^{k} λ_{j}

(11)

III.FISHERFACE METHOD

A.THE DEFINITION OF FISHERFACE

When Fisherface criterion function is used to solve the optimal set of discriminant vectors, one of the inherent conditions is to require the within-class scatter matrix to be nonsingular [33]. To ensure that this condition holds, the number of samples participating in training cannot be less than the dimension of samples. In fact, in the process of human ear recognition experiment, the number of training samples is far less than the dimension of the original samples. In this case, the within-class scatter matrix is singular, so the LDA method cannot be used directly. This kind of problem is called the small-sample problem. When the problem of small sample exists, the corresponding within-class scatter matrix is singular, and the value of ${s_{w}}^{- 1}$ cannot be obtained directly. In the case of small sample problem, the key to feature extraction is to obtain the optimal discriminant vector set by using fisher criterion. Fisherface is the most typical method to solve this problem.

B.THE ALGORITHM PROCESS

(1)Using PCA to reduce the dimension, that is, taking the K-L transformation $y_{i}^{(j)} = P^{T} x_{i}^{(j)}$ for all samples $x_{i}^{(j)}$ , By compressing the original samples with higher dimensions to the lower dimensions, the within-class scatter matrix ${\tilde{s}}_{w}$ of the samples with reduced dimensionality is invertible. The column vectors $p_{1}, p_{2} \dots p_{N - C}$ in matrix $P$ are the set of eigenvectors corresponding to the first $N - C$ non-zero maximum eigenvalues of the total scatter matrix $S_{t}$ .
(2)In the transformed space, Fisherface discriminant analysis method is used to extract features. After dimensionality reduction, the between-class scatter matrix and within-class scatter matrix of samples are expressed as ${\tilde{s}}_{b} = P^{T} S_{b} P$ and ${\tilde{s}}_{w} = P^{T} S_{w} P$ , respectively. If ${\tilde{s}}_{w}$ is non-singular, the column vectors in the optimal projection matrix ${\tilde{A}}_{opt}$ take the eigenvectors corresponding to the first $d$ largest eigenvalues of ${\tilde{S}}_{w}^{- 1} {\tilde{S}}_{b}$ , and the eigenvectors are ${\tilde{a}}_{1}, \dots {\tilde{a}}_{d}$ .
(3)Finally, the projection matrix of feature extraction is directly applied on the original sample is $A_{opt} = P {\tilde{A}}_{opt}$ .

IV.THE COMPLEMENTARY DOUBLE FEATURE EXTRACTION ALGORITHM BASED ON PCA AND FISHERFACE

A.THE IDEA OF ALGORITHM

The key of the complementary double feature extraction algorithm proposed in this paper is to divide the human ear test samples into two parts. One part is easy to recognize in a subspace, the other counterpart is difficult to recognize in this subspace, and the other counterpart of human ear test samples that are difficult to recognize are projected into the complementary subspace for recognition. In order to realize the complementary double feature extraction algorithm, it is necessary to first adopt the pre-classification method in the feature subspace generated by PCA. First, the test samples are divided into two parts. One part is easy to recognize and the other counterpart is difficult to recognize in a feature subspace. The specific method is to pre-classify the test samples by using two different classifiers at the same time and then fuse the classification results of human ear samples. When the classification results of the two different classifiers are the same, this part of the human ear test sample is considered to be easy to be classified, and the result is regarded as the pre-classification result of human ear test sample. When the classification results of the two different classifiers are different, the test sample is considered to be difficult to be classified in the feature subspace generated by PCA. Then, the human ear test samples that are difficult to classify are projected into the feature subspace generated by Fisherface for classification and recognition. The principle structure block diagram of the algorithm is shown in Fig. 1.

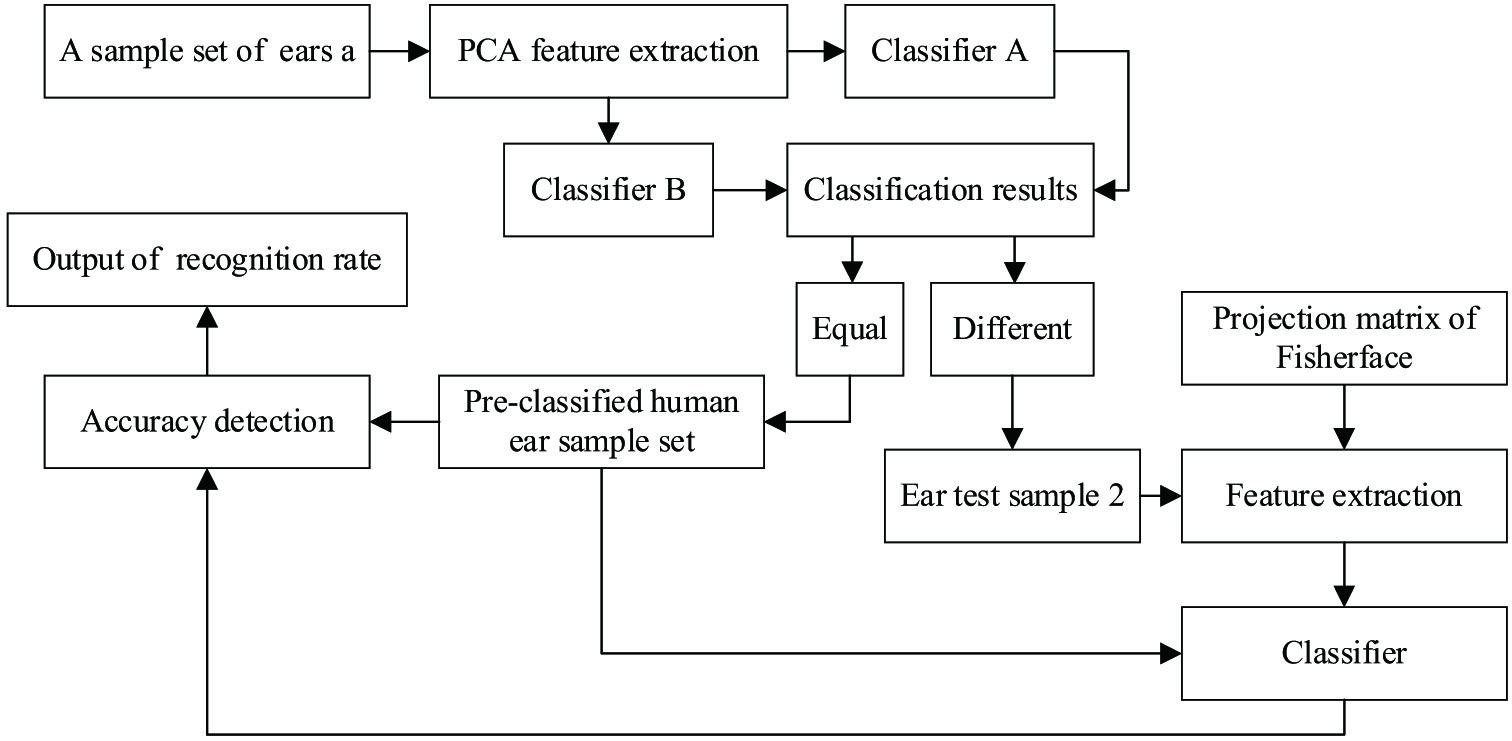Fig. 1. Principle block diagram of PCA and Fisherface complementary double feature extraction algorithm.

It can be seen from Fig. 1 that the complementary double feature extraction algorithm uses a variety of classifiers to achieve the pre-classification of human ear test samples. After pre-classification, the test samples in the pre-classification sample set also have category identification, just like the training samples. Pre-classification can divide the human ear test sample set into two parts, pre-classification human ear sample set, which is composed of test samples with the same pre-classification results, and human ear test sample set 2, which are composed of test samples with the different pre-classification results. When classification is in progress, the Fisherface projection matrix is generated using the ear training samples. Then, the features of ear samples in test sample set 2 were extracted, and the pre-classified sample set was used to optimize classifier 3. Then, the test sample set 2 was classified and identified, and test the accuracy of classification results and pre classification results together. Finally, it is output in the form of recognition rate.

B.THE ALGORITHM

Suppose there are C types of human ear patterns, namely $w_{1}, w_{2}, \dots w_{c}$ . There are $N_{i}$ training samples for each category indicated, $i = 1, 2, … C$ . The total number of test samples is $T$ , so the algorithm of this paper is as follows:

(1)Pattern feature extraction based on PCA: feature extraction is carried out in the subspace generated by PCA to obtain feature vectors, which is shown in formula (12).
$X_{p} = {{(x_{p})}^{k}, k = 1, 2, …… T}$ (12)
In formula (12), $X_{p}$ represents the test sample set after feature extraction using PCA, and subscript P represents the feature subspace of PCA.
(2)Work process of pre classification: two different classifiers are used to pre classify ear pattern feature vectors, namely, the following two categories, as shown in Formula (13).
$X_{p}^{1} = {{(x_{p})}_{i}^{k}, i = 1, 2, …. C; k = 1, 2, …… T} X_{p}^{2} = {{(x_{p})}_{j}^{k}, j = 1, 2, …. C; k = 1, 2, …… T}$ (13)
In formula (13), ${(x_{p})}_{i}^{k}$ and ${(x_{p})}_{j}^{k}$ indicate that the $k$ -th unknown sample is identified as Class $i$ and Class $j$ respectively.
(3)Fusion of classification results: the classification results of two different classifiers are fused, and the test samples with the same classification results are combined into a new set $X_{a}$ , that is, the pre-classification sample set. The test samples with different classification results are formed into another set $X_{b}$ , If $i = j$ , put ${(x_{p})}_{i}^{k}$ in the $X_{a}$ set, otherwise put it in $X_{b}$ , as shown in Formula (14).
(14)
(4)Calculate the Fisherface projection matrix: directly calculate the Fisherface projection matrix using ear training samples.
(5)The second feature extraction (also called complementary feature extraction): the Fisherface projection matrix is used to project the test samples in the test sample set $X_{b}$ , that is, the ear test samples that are difficult to recognize in the feature subspace generated by PCA, which are projected into the Fisherface feature subspace.
(6)Classifier $c$ is used for classification: the test samples in test sample set $X_{b}$ are classified and recognized.
(7)Accuracy detection: the classification result of classifier $c$ and the pre classification sample set $X_{a}$ are used for accuracy detection, and the detection results are output in the form of pattern recognition rate.

V.EXPERIMENTAL RESULTS AND ANALYSIS

The experimental environment is as follows: the system is Inter(R) Core^™ i7 CPU @ 1.80 GHz 2·00 GHz, the hard disk is 256G + 1T, the operating system is Windows10, the algorithm program was run on PyCharm 2019.1.3x64.

Since the human ear image library built by the ear image laboratory of the School of Information Engineering of University of Science and Technology Beijing is open to the public, in this paper, the PCA and Fisherface complementary double feature extraction algorithm is tested using the ear image library. The experiment is conducted on two human ear image databases. First, a brief introduction to these two ear image databases is given as follows:

Ear image library I: It was shot in 2002, including 60 people, each of whom has 3 right ear images, including 1 frontal image, 1 slight angle change, 1 light change, and 256 gray levels. The ear images were rotated and cut without light compensation, as shown in Fig. 2.

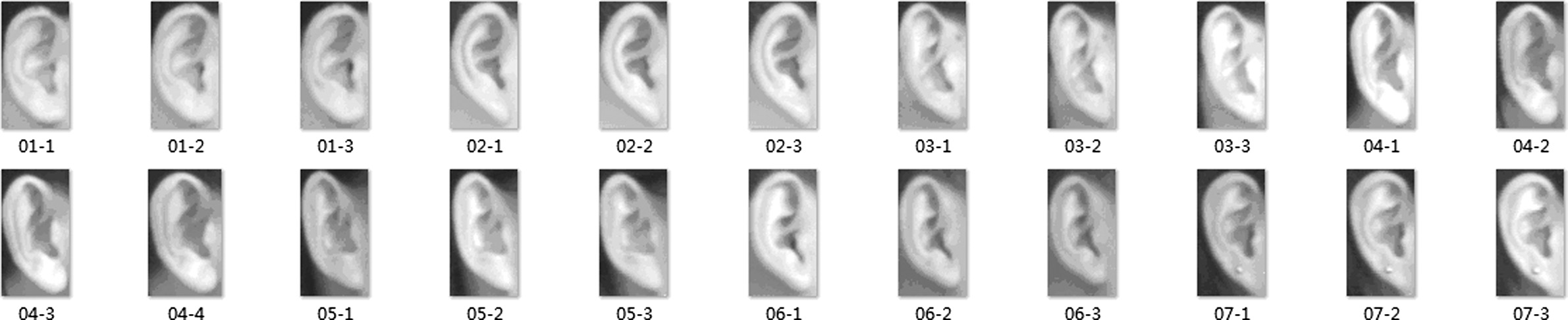Fig. 2. Ear image library I (1 frontal image, 1 slight angle change image, 1 light change image).

Ear image library II: It was shot in 2003, including 77 people, each of whom has 4 right ear images, including 1 frontal image, 2 rotated images, and 1 light change image. The ear images have been cut and processed. The images in the library are relatively consistent with the actual situation, as shown in Fig. 3.

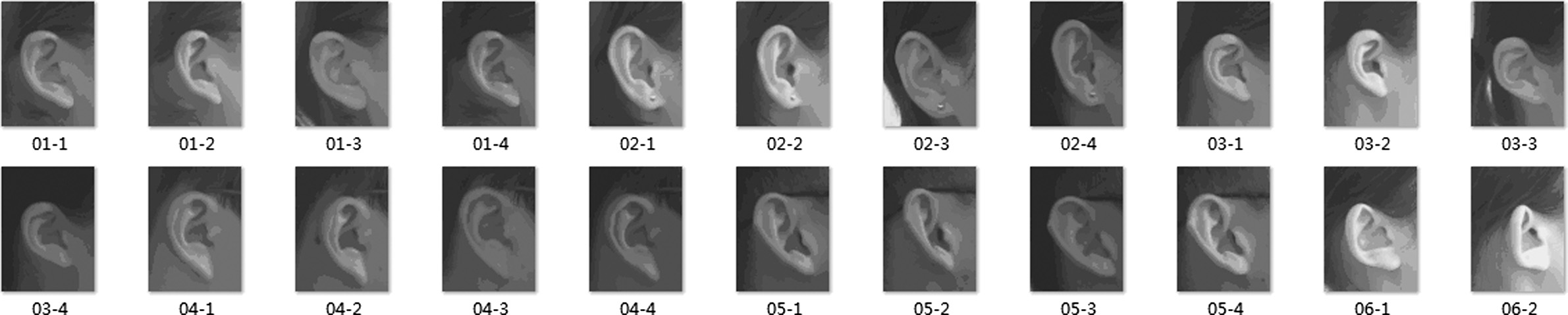Fig. 3. Ear image library II (1 frontal image, 2 rotated images,1 light change image).

A.EXPERIMENT 1

First, the images in the human ear library are preprocessed, the preprocessing includes histogram equalization and size normalization. PCA, Fisherface, ICA are used for feature extraction. In the experiment, the first two images in the ear image library I are used as training samples, the third image is used as test sample, the first three images in the ear image library II are used as training samples, and the fourth image is used as test sample. PCA, Fisherface, ICA are used for feature extraction, and then nearest neighbor classifier, support vector machine classifier (SVM) and minimum distance classifier are used for classification and recognition respectively. For the selection of kernel function in SVM, we choose Gaussian kernel function, because the effect is usually the best, and the number of parameter adjustments is relatively small, which is more convenient. For the selection of K parameter value in the nearest neighbor classifier, we take a higher value, which has a smoothing effect and makes the classifier more resistant to outliers. The experimental results are shown in Table I.

Table I. Comparison of classification and recognition accuracy of PCA, Fisherface and ICA

Ear image library	Feature extraction method	Classifier	Recognition rate (%)	Recognition time (s)
Ear image library I	PCA	Nearest Neighbor	87.43	0.035
		SVM	92.38	0.121
		Minimum Distance	90.31	0.018
Ear image library II	PCA	Nearest Neighbor	83.53	0.358
		SVM	93.46	0.092
		Minimum Distance	92.47	0.089
Ear image library I	Fisherface	Nearest Neighbor	85.21	0.045
		SVM	86.79	0.176
		Minimum Distance	91.38	0.086
Ear image library II	Fisherface	Nearest Neighbor	89.23	0.043
		SVM	82.46	0.067
		Minimum Distance	90.14	0.086
Ear image library I	ICA	Nearest Neighbor	94.84	0.067
		SVM	93.32	0.186
		Minimum Distance	92.98	0.124
Ear image library II	ICA	Nearest Neighbor	95.13	0.143
		SVM	93.86	1.973
		Minimum Distance	94.14	0.243

As can be seen from Table I, when PCA and Fisherface are used alone for feature extraction, the recognition rate of the classifier is not very high. When PCA is used for feature extraction, the recognition rate of the nearest neighbor classifier is lower than 90%. The recognition is not good too. The main reason is that in the process of constructing PCA feature subspace, the weights of each dimension are different, and their weights are arranged from large to small according to the eigenvalues of the overall dispersion matrix of the training samples. In the design of classifier, SVM will find the feature dimension that contributes the most to the classification interval and assign different weights. It conforms to the characteristics of PCA feature space. In the nearest neighbor classifier, each dimension of the feature has the same contribution to the distance, and they are considered to have the same weight value. This is the reason why the recognition rate of the nearest neighbor classifier is not high in the feature space based on PCA. However, the recognition rate of ICA single feature extraction is significantly higher than that of PCA and Fisherface, mainly because the important information needed in ear recognition may contain the high-order statistical relationship between pixels, while ICA feature extraction is the high-order information between pixels, and each feature is independent of each other.

B.EXPERIMENT 2

The experiment of the complementary dual feature extraction algorithm overcomes the limitations of the single feature extraction algorithm. The experimental environment in Experiment 2 is exactly the same as that in Experiment 1. When PCA algorithm is used for single feature extraction, the classification recognition rate of using support SVM and minimum distance classifier is high. We consider two different classifiers, SVM and minimum distance classifiers, which are used for pre-classification. Furthermore, human ear test samples are divided into two parts, one part is easy to recognize and the other counterpart is difficult to recognize. As the complementary space of PCA, Fisherface is used to project the hard to identify human ear image into the space for the second feature extraction. For Fisherface feature extraction, the nearest neighbor classifier is used, and the experimental results are shown in Table II.

Table II. Classification and recognition accuracy of complementary double feature extraction

Ear image library	Feature extraction method	Classifier	Recognition rate (%)	Recognition time (s)
Ear image library I	PCA + Fisherface	Nearest Neighbor	98.18	0.155
		SVM	95.13	0.186
		Minimum Distance	96.16	0.393
Ear image library II	PCA + Fisherface	Nearest Neighbor	97.63	0.262
		SVM	96.87	0.369
		Minimum Distance	94.62	0.182

It can be seen from Table II that the recognition rate of the complementary dual feature extraction method is significantly higher than that of the principal component analysis (PCA), Fisherface and independent component analysis (ICA) single feature extraction shown in Table I. This is mainly to project the human ear samples that cannot be identified in the PCA single feature space to the Fisherface space for the second feature extraction. Thus, there is a lot of room to improve the recognition rate. These data again proves the effectiveness of the PCA and Fisherface complementary dual feature extraction method in improving the ear recognition rate. Although the recognition time increases correspondingly, the increase is within the range of affordability, and thus it directly verifies the practicability of this algorithm. The key of this experiment is to adopt the method of pre classification, divide the ear test samples into two parts, one part is easy to recognize and the other counterpart is difficult to recognize, and project the human ear test samples that are difficult to identify into the complementary feature subspaces for feature extraction again, and classification recognition, which can better overcome the limitations caused by the relatively low recognition rate of single feature extraction of principal component analysis, Fisherface and independent component analysis.

VI.CONCLUSIONS

Human ear recognition technology is a new biometric recognition technology, which has received widespread attention in recent years. This technology has the advantages of high stability, high reliability and relatively small amount of data to be processed. At the same time, it is also a non-interference recognition technology, which has become a popular research direction of the biometric recognition. Ear recognition can complement face, fingerprint, iris, gait and other biometric recognition technologies to improve the identification accuracy of individual identity recognition, and can also be used for individual identity authentication, enriching the content of biometric recognition field. The key link in human ear recognition technology is feature extraction, which determines the success of human ear image recognition to a large extent. Currently, feature extraction methods can be classified into two categories: one is feature extraction based on geometry, the other is feature extraction based on algebra. The feature extraction algorithm in this paper is an improvement of the feature extraction algorithm based on algebra.

In this paper, an ear image recognition method based on complementary dual feature extraction was proposed, which overcame the disadvantages of many human ear images recognition methods. First, according to the separability of the pattern feature vector, the human ear test samples were divided into two parts. Furthermore, one part is easy to recognize and the other counterpart is difficult to recognize in a feature subspace. In our approach, the complementary space of the PCA feature extraction space was searched, using Fisherface as the complementary space, and using Fisherface as the complementary space is mainly using the best discriminative information of pattern as the complementary information of the optimal representation of the pattern. In this way, it could avoid the grave consequence that the classification performance may drop sharply if different feature vectors were fused together. From the experimental results of the algorithm proposed in this paper, it could be seen that using the complementary dual feature extraction could obtain a very high pattern recognition rate, and this algorithm had high practicality. The key of the complementary dual feature extraction algorithm in this paper was to find two feature subspaces with complementarity. At present, there are many feature extraction methods for pattern recognition. Our next step is to find a better complementary dual feature extraction combination algorithm, so that it can be applied to ear image recognition to further improve the recognition rate. In addition, improving the recognition rate of human ear images with attitude angle changes is also the focus of the next step of research. We can consider using the useful information that the physiological positions of human ears and faces are close to each other to carry out a variety of biological features fusion, and then improve the recognition rate of human ear images with attitude angle changes.

Human Ear Image Recognition Method Using PCA and Fisherface Complementary Double Feature Extraction