JAIT

I.INTRODUCTION

The base of various image processing applications is the data collection in the way of digital images. Higher standards of image processing are essential in numerous science and engineering fields, whether seen from the perspective of human or machine vision. A precise and reliable data collection is key to enhancing all image types with enhanced quality [1–3]. The images captured in low-light circumstances cause degradation such as higher noise, low brightness, and low contrast. The degraded images create difficulty in different essential tasks such as object detection, semantic segmentation, and object tacking. Hence, it is essential for developing an appropriate image enhancement approach to obtain an image with enhanced quality from degraded inputs [4–6]. On the other hand, the camera movement or lens defocusing also caused blurred images [7,8]. The profile of blur is mainly based on the intensity dissemination that is related to the spreading of point images in the blur area [9].

Image restoration and representation are considered two challenging tasks in computer vision. Image restoration is the process of reforming a high-quality image from degraded versions, e.g., blurry and noisy. In image representation, the sparse coding enabled an effective representation of signals with only fewer active elements [10]. Image restoration also referred to as image in painting where the automatic restoration of the damaged image region is accomplished; therefore, the image is obtained is naturally and a person who is not familiar with the original image cannot observe the restoration [11]. Image deblurring aims to achieve a sharp image by eliminating the blur from a degraded image. Image deblurring is one of the common steps; however, it is highly mandatory in the computer vision field [12–14]. The low frame rates/low shutter speeds, object motions, and camera shakes are affected image/video quality which resulted in information loss. Elimination of such blurring is used to restore the image that is used in numerous applications such as moving object segmentation, text recognition, facial detection, and so on [15]. Image restoration is highly complex to resolve or achieve a single result because of ill-posed character issue [16]. The aforementioned limitations are considered as a motivation for this research to perform an effective image deblurring and restoration.

The contributions are concise as follows:

•The MORSA is used in this research for performing effective threshold and kernel parameter computations. The reptile search algorithm (RSA) is chosen mainly because of its effective equilibrium between exploitation and exploration.
•The threshold from MORSA is used to perform the noise removal DRN, where noisy pixels are identified and replaced with new pixels. Further, the kernel estimation along with MORSA was performed to enhance the deblurring process.

The paper is sorted as follows: Section II gives the existing research related to the image restoration and deblurring process. The image deblurring and restoration using MORSA are detailed in Section III. The results of the proposed method are given in Section IV. Moreover, the Discussion and Conclusion of this research are given in Sections V and VI.

II.RELATED WORK

The existing research developed for performing the image deblurring and restoring is given in the following section.

Sadok, et al. [17] developed a regularized dispersion particle filter (RDPF) to accomplish restoration. The developed RDPF depends on the Hidden Markov Model (HMM) and the utilization of the exponential dispersion unit and expectation maximization (EM) approach. The EM and Newton Raphson approach were used to calculate the unknown variance noise and dispersion parameters. The extended EM developed in this work was used to deal with non-Gaussian noise. On the contrary, the developed RDPF was required a huge amount of iterations to restore the image.

Malik, et al. [18] presented a Self-Operational Neural Network (ONN) for handling image restoration issues. This Self-ONNs have generative neurons that have the capacity for synthesizing the nodal operator by leveraging Taylor polynomials. The Self-ONN offers an optimal balance among the number of parameters and performance of denoizing than the convolutional networks. The denoizing using Self-ONN mainly depends on the weight values, whereas the performance was degraded when the weight was less in the network.

Hu, et al. [19] developed enhanced local maximum intensity (ELMI) prior for deblurring the image. This ELMI was the combination of local maximum gradient (LMG) prior and local maximum intensity (LMI) prior. The ELMI was motivated by the principle of the high value of local patch pixels, and gradients were reduced along with the blurring process. The integration of LMG into LMI was used to enhance the latent image as well as it was useful in kernel estimation. However, the developed ELMI incorporated a huge amount of nonlinear operations while deblurring the image.

Li, et al. [20] presented the interpretable neural network structure namely deep unrolling for blind deblurring (DUBLID) approach. The DUBLID depends on the recasting of a generalized total variation regularized methodology in a neural network and their parameter optimization through custom backpropagation. The developed DUBLID has the advantage of interpretability as well as this DUBLID recovered the kernel similar to the ground truth. The DUBLID was required to incorporate the noisy pixel discovery for improving the deblurring performances. However, an extra hardware support such as graphics processing unit (GPU) was required for faster deblurring process.

Eqtedaei, A. and Ahmadyfard, A [21] developed multiscale approach according to the maximum a posterior (MAP) structure to perform the image motion deblurring. In this MAP-based approach, the blurry image was represented in various scales. The k-means clustering was used to segment an each scale of the image. For an each scale, the blur kernel was computed by utilizing the image data in dominant edges. From the coarser levels in a coarse-to-fine manner, the blur kernel was computed in pyramid’s finest level. The developed MAP-based approach does not require complex considerations for estimating the intermediate latent image. The time consumption was high, when the sharp image was recovered in pyramid’s finest level.

Zhao et al. [22] presented an image-deblurring context-aware multiscale convolutional neural network namely CDMC-Net. Two different stages such as multiscale network and cross stage feature aggregation (CSFA) were developed for restoring the latent sharp images, whereas CSFA was used for improving the information flow communication. The multiscale blurry images were processed in a coarse-to-fine manner. Moreover, the multistrip feature extraction was used to obtain long-range context information in various scenarios. The developed neural network failed to deblur the low-light images because strong edges of image were mistakenly considered as structural edges.

The literature survey along with the advantages and limitations is given in the following Table I.

Table I. Literature survey

Author name	Proposed method	Advantages	Limitations
Sadok, et al. [17]	The restoration of images was achieved by using the RDPF filter.	The non-Gaussian noise was handled by using the extended EM in RDPF.	The developed RDPF required a huge amount of iterations to restore the image.
Malik, et al. [18]	The Self-ONN with generative neurons was developed to handle the image restoration issues.	The tradeoff among the number of parameters and performance of denoizing were achieved by Self-ONN.	The weight values of Self-ONN decide the denoizing performances during image restoration.
Hu, et al. [19]	The ELMI which is the combination of LMG and LMI prior was developed for deblurring the image.	The latent image was improved by using the integration of LMG and LMI.	The ELMI required a huge amount of nonlinear operations while deblurring the image.
Li, et al. [20]	The interpretable neural network structure, i.e., DUBLID, was developed for image deblurring process.	The developed DUBLID recovered the kernel similar to the ground truth because of its interpretability.	An extra hardware support such as graphics processing unit was required for faster deblurring process.
Eqtedaei, A. and Ahmadyfard, A [21]	The multiscale approach according to the MAP structure was developed to perform the image motion deblurring	The developed MAP-based approach does not require complex considerations for estimating the intermediate latent image.	The time consumption was high when the sharp image was recovered in pyramid’s finest level.
Zhao et al. [22]	A context-aware multiscale convolutional neural network (CDMC-Net) is developed for deblurring the image.	The context information from different scenarios were obtained by using the multistrip feature extraction.	However, the CDMC-Net failed to deblur the low light images because strong edges of image were mistakenly considered as structural edges.

The limitations found from related work are inefficient deblurring for low-light images and higher time consumption for sharp images. The noisy pixel discovery is essential for an effective deblurring over the images. The DRN is used in this research to identify the noisy pixels. Next, the MORSA is used in two different processes such as threshold calculation for noise removal and kernel estimation. After computing the threshold values, the noisy pixels are deblurred by using the kernel estimation. Further, the salient edges information is used to estimate the noisy kernel in less time for sharp images.

III.PROPOSED METHOD

The MORSA is developed for performing image restoration and deblurring to improve the PSNR. In general, the meta heuristic algorithm has the best learning strategy, so it is considered for automatic selection of optimal threshold instead of manual calculation. Therefore, this research considered the MORSA to ensure the selection of best threshold values. The MORSA is used in two different stages such as threshold calculation for noise removal and kernel estimation. The threshold computation using MORSA is used to effectively discover and remove the noisy pixel using DRN. Further, MORSA is also used in the kernel estimation to deblur the image by computing the optimal kernel parameters. The block diagram of the proposed method is shown in Fig. 1.

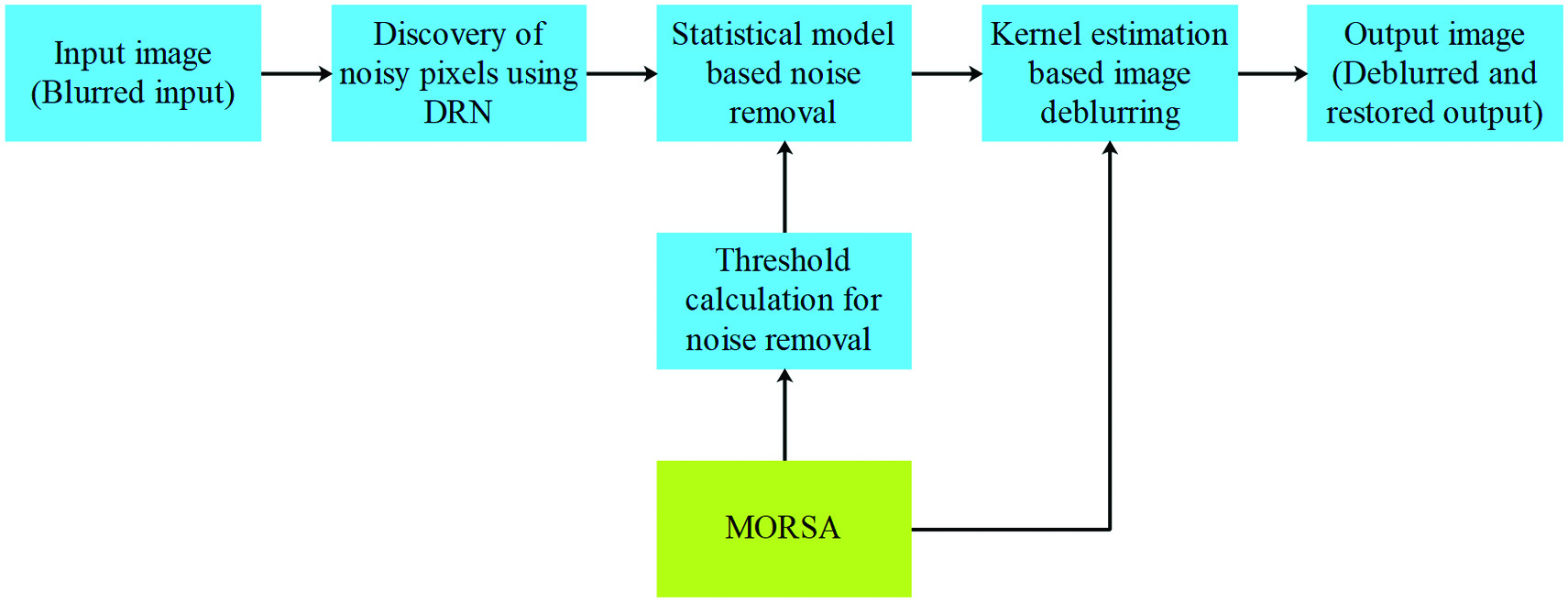Fig. 1. Block diagram of the proposed method.

A.DATA ACQUISITION AND DISCOVERY OF NOISY PIXELS USING DRN

Consider the image obtained from the database is $H$ with the dimension of $U \times V$ , and it is given as input to noisy pixel identification. The recording process creates different irrelevant consequences such as blurring and noise in the images observed in various situations. The location of the pixel for the input image $(H)$ is represented as $H (u, v)$ . The noisy pixels are discovered by using a deep residual network (DRN), which has various layers such as residual blocks, convolutional (Conv), intermediate pooling, and the linear classifier.

The steps processed in the DRN are provided as follows:

•The computation process of Conv layer is expressed in equations (1) and (2).
$B 2 d (H) = \sum_{a = 0}^{E - 1} \sum_{s = 0}^{E - 1} X_{a, s} . H_{(u + a), (v + s)}$ (1)
$B 1 d (H) = \sum_{Z = 0}^{C_{i n} - 1} X_{Z} * H$ (2)

where the recording coordinates are denoted as

u

and

v

;

X

denotes the kernel matrix

E \times E

, which also referred as learnable parameter; the kernel matrix’s position index is denoted as

a

and

s

; the size of kernel for input neuron

Z

is denoted as

X_{Z}

, and cross-correlation operator is denoted as

*

•Next, the pooling layer is incorporated among Conv layer, and it is used for minimizing the feature map’s spatial size. Each slice and depth of feature map were operated by selecting the average pooling layer.
•The DRN uses the rectified linear unit (ReLU), i.e., the nonlinear activation function that is used to process the image. Equation (3) expresses the ReLU function.
$R e L U (H) = {\begin{cases} 0; & K < 0 \\ K; & K \geq 0 \end{cases}$ (3)

where feature is denoted as

K

•The input layers are normalized in batch normalization function by scaling and adjusting the activation functions for enhancing the training speed and reliability.
•The shortcut link among the Conv layers is referred by residual blocks. The input is attached with output, when the input and output are same. If the dimensions are different, the dimension matching factor is used to match the input and output.
•The linear classifier discovers the noisy pixels from the input image, once the process of the Conv layer is done in DRN.

B.STATISTICAL MODEL-BASED NOISE REMOVAL

A new pixel is identified for each noisy pixel by using the statistical model. Equation (4) is used to eliminate the noise pixel, when it is deliberated as a noise pixel.

H^{γ} (u, v) = {\begin{array}{c} H^{c} (u, v) & i f B (u, v) = 1 \\ H (u, v) & O t h e r w i s e \end{array}}

(4)

where the new pixel value is denoted as

H^{c} (u, v)

. The chosen noise pixels are utilized for computing the new pixel value. Initially, a

H (r, q)

, i.e.,

3 \times 3

window is generated based on noisy pixels followed by it is evaluated with the input image

H (u, v)

. Equivalent pixel value is chosen and denoted as

A

by evaluating the image

H (r, q)

with

H (u, v)

. These matched pixels are utilized for further processes. The new pixel value is calculated, when the

A

is higher than the threshold

s_{1}

. Otherwise, the noise pixel is interchanged with the original input image in the chosen

3 \times 3

window. The parameters such as

X_{d}, R

and

J

are used to create the new pixel value by utilizing the

f (u, v)

as shown in equation (5).

f (u, v) = F (X_{d}, R, J)

(5)

where the initial value is chosen by

X_{d}

is denoted as

J

and the absolute function calculated utilizing the adjacent pixel value is denoted as

R

is expressed in equation (6).

R = a b s (H (r, q) - H (r + u - 3, q + v - 3))

(6)

The $X_{d}$ is discovered by a prefixed window according to the absolute result. But, the $X_{d}$ is fixed as zero where $d$ differs according to the prefixed window $η$ that is shown in equation (7).

X_{d} = X_{d} + (E_{1} (u, v) \times R) 1 \leq d \leq n

(7)

A $X_{d}$ ’s rounding process is computed as round $(X_{d} / 8)$ that is denoted as $b$ . For $X_{d}$ , the process of sorting is estimated such that the preliminary value $X_{d}$ is chosen as $J$ . Equation (5) is rewritten as shown in equation (8).

f (u, v) = {\begin{cases} 1 - \frac{(J - 1)}{4}; & J > 10 \\ 1 & ; & O t h e r w i s e \end{cases}

(8)

The $f (u, v)$ is compared with the threshold $s_{2}$ . A function $G$ is created, when the $f (u, v) > s_{2}$ as shown in equation (9).

G = {\begin{cases} s u m (\frac{α . χ}{c_{1}}) & ; & w > s_{3} \\ f (u, v) & ; & O t h e r w i s e \end{cases}

(9)

where the mean value of the adjacent pixel is denoted as

χ

, and

c_{1}

is fixed as

4

. The new pixel is calculated based on equation (10), when

G > s_{3}

H^{c} (u, v) = \frac{G_{U}}{G_{V}} = \frac{\sum (H (u, v) . B (u, v))}{\sum B (u, v)}

(10)

The threshold parameters of the statistical models such as $s_{1}, s_{2}$ , and $s_{3}$ are calculated using the MORSA algorithm.

C.THRESHOLD CALCULATION FOR NOISE REMOVAL USING MORSA

In this phase, MORSA is used for discovering the optimal values of the threshold for the statistical model. For an effective computation of new pixels, it is essential to select the threshold values for noisy pixels. In general, the conventional RSA is motivated by the encircling, hunting, and social behavior of crocodiles. The iterative process of MORSA and its objective function calculation are detailed in the following sections.

1)ITERATIVE PROCESS OF MORSA

In MORSA, the exploration and exploitation are obtained by the motion of the crocodile while encircling the target prey. The parameters of MORSA are mentioned as follows: population size = 50, dimension = 3, and iterations = 150. There are two different kinds of motions such as high and belly walking based on encircling actions during the exploration phase. Equation (11) represents the location update of MORSA. If iteration $(t)$ is lesser than the $T / 4$ , the high walking is initialized, where $T$ defines maximum iteration; otherwise, the belly walking is done as per equation (11).

y_{(i, j)} (t + 1) = {\begin{array}{ll} y_{j}^{*} (t) \times - ϕ_{(i, j)} (t) \times μ - R F_{(i, j)} (t) \times r, & t \leq \frac{T}{4} \\ y_{j}^{*} (t) \times y_{(r_{1}, j)} \times E S (t) \times r, & t \leq 2 \frac{T}{4} a n d t > \frac{T}{4} \end{array}

(11)

where

y_{(i, j)}

is position

j

of solution

i

; the best solution is denoted as

y_{j}^{*} (t)

; the random value among

[0, 1]

r

; the hunting parameter is

ϕ_{(i, j)} (t)

that is formulated in equation (12);

μ

is set to 0.1;

R F_{(i, j)}

is reduce function, which is expressed in equation (13);

r_{1} - r_{4}

are random numbers;

y_{(r_{1}, j)}

are random location; and the evolutionary sense

E S (t)

is expressed in equation (14);

φ_{(i, j)} = y_{j}^{*} (t) \times D V_{(i, j)}

(12)

R F_{(i, j)} = \frac{y_{j}^{*} (t) - y_{(r_{2}, j)}}{y_{j}^{*} (t) + ε}

(13)

E S (t) = 2 \times r_{3} \times (1 - \frac{1}{T})

(14)

where

ε

is a small value and

D V_{(i, j)}

denotes the difference value expressed in equation (15).

D V_{(i, j)} = α + \frac{y_{(i, j)} - M (y_{i})}{B_{j} (t) + (U B_{j} - L B_{j}) + ε'}

(15)

where an average location is denoted as

M (y_{i})

, and it is expressed in equation (16). A lower and upper limits of MORSA are

L B_{j}

and

U B_{j}

, and

α

is fixed as

0.1

M (y_{i}) = \frac{1}{n} \sum_{j = 1}^{n} y_{(i, j)}

(16)

Next, the exploitation, i.e., hunting is accomplished that used two approaches such as hunting coordination and hunting collaboration. The MORSA performs the hunting coordination when the condition of $t \leq 3 \frac{T}{4}$ and $t > 2 \frac{T}{4}$ are satisfied; otherwise, the hunting cooperation takes place as shown in equation (17).

y_{(i, j)} (t + 1) = {\begin{cases} B_{j} (t) \times P_{(i, j)} (t) \times r, & t \leq 3 \frac{T}{4} a n d t > 2 \frac{T}{4} \\ B_{j} (t) - ϕ_{(i, j)} (t) \times ε - R F_{(i, j)} (t) \times r, & t \leq T a n d t > 3 \frac{T}{4} \end{cases}

(17)

The iteration of MORSA is repeated until the specified iteration is met, or the best solution is obtained in the selection process. The computational complexity of MORSA is $O (T \times P S \times D i m)$ , where $T$ defines maximum iteration;population size is denoted as $P S$ , and dimension is denoted as $D i m$ . The objective function used to find the optimal threshold is derived in the following section.

2)OBJECTIVE FUNCTION OF MORSA FOR NOISE REMOVAL

The optimal threshold for noise removal is chosen according to the objective function expressed in equation (18). The solution with a lesser value is selected as the optimal solution, i.e., optimal threshold values for the statistical model.

O b j 1 = N [τ \times I_{c o n t} + \log (R (J (G), G))]

(18)

where

O b j 1

denotes the objective function for noise removal; the hyperparameter is denoted as

τ

; the first term denotes the generative subnetwork to obtain enhanced output that is close to the images with higher contrast and the second term offers enhanced outcome which is indistinguishable from images with higher contrast. The derived fitness function is used to find the optimal threshold of

s_{1}, s_{2}

, and

s_{3}

for a statistical model. After that, it was used to perform noise removal.

The Pseudo code for MORSA-based threshold calculation is shown in Algorithm 1.

Algorithm 1: MORSA-based threshold calculation.

Input: Noisy central pixel

Output: Computation of threshold values based on the proposed MORSA

Initialize the population

Fitness function evaluation

While (end criteria failed to satisfy)

For each population

Update the solution

End for

Fitness function evaluation

Find the best solution

Update the population

End while

Best solution is returned

D.KERNEL ESTIMATION-BASED IMAGE DEBLURRING

After removing the noisy pixels, the image is further processed by image deblurring, which is accomplished by kernel estimation. The estimation of kernel is represented in equation (19) according to the hyper-Laplacian model.

\min_{g} ‖ {\nabla H^{c} - g \times \nabla K ‖}_{2}^{2} + p ‖ {g ‖}_{x}^{x}; g (z) \geq 0, \sum_{z} g (z) = 1, 0 < x \leq 1

(19)

The aforementioned equation (19) is used to preserve the sparsity; however, it does not display the blur kernel’s continuity. The noisy kernel is estimated using the salient edges $\nabla K$ . The term $N (g)$ expressed in equation (20) is used to control the gradients to preserve the kernel continuity.

N (g) = # {z | | \partial_{z} g (z) + | \partial_{k} g (z) | \neq 0 |}

(20)

Where an amount of the pixel with nonzero gradients is denoted as $N (g)$ . Accordingly, the estimation of the kernel is written as shown in equation (21).

\min_{g} {‖ \nabla H^{c} - g \times \nabla K ‖}_{2}^{2} + p {‖ g ‖}_{x}^{x} + σ N (g); g (z) \geq 0, \sum_{z} g (z) = 1

(21)

where the parameter utilized for controlling the smoothness

g

is denoted as

σ

. Equation (21) is modified as shown in equation (22). Further, it is minimized with the iterative reweighted least square as shown in equation (23).

\min_{g} {‖ \nabla H^{c} - g \times \nabla K ‖}_{2}^{2} + p {‖ g ‖}_{x}^{x}; g (z) \geq 0, \sum_{z} g (z) = 1

(22)

\min_{g} {‖ \hat{g} - g ‖}_{2}^{2} + σ . N (\hat{g})

(23)

Further, the parameters of $p$ and $σ$ are also identified by using the same MORSA, and the objective function for kernel estimation is given in the following section.

E.OBJECTIVE FUNCTION FOR KERNEL ESTIMATION

The iterative process of kernel estimation using MORSA is similar to “Kernel Estimation-based Image Deblurring.” A quadratic programming function is used to calculate the objective measure for creating a matrix. Consequently, the search agents are evaluated by utilizing the objective function for kernel estimation $(O b j 2)$ as expressed in equation (24).

O b j 2 = 0.5 \times H \times D \times H^{'} + C F' \times H^{'}

(24)

where the matrix is denoted as

D

and the coefficient function’s transpose is denoted as

C F'

IV.RESULTS AND DISCUSSION

This section provides a comparison of the proposed method with the existing methodologies. The proposed method is developed and executed in MATLAB R2020a, which is operated under 16GB RAM and an i5 core processor. The proposed method is used to accomplish image representation and restoration by deblurring the images. Here, the performances are evaluated in terms of PSNR and SSIM, which are expressed in equations (25) and (26).

P S N R = 10 \log_{10} (\frac{m_{m a x}^{2}}{M S E})

(25)

S S I M (e, h) = \frac{(2 η_{e} η_{h} + φ_{1}) (2 ξ_{e h} + φ_{2})}{(η_{e}^{2} + η_{h}^{2} + φ_{1}) (ξ_{e}^{2} + ξ_{h}^{2} + φ_{2})}

(26)

where the maximum image pixel value is denoted as

m_{m a x}

; mean square error is denoted as

M S E

; pixels are denoted as

e

and

h

; mean pixel value is denoted as

η_{e}

and

η_{h}

; pixel variance is denoted as

ξ_{e}

and

ξ_{h}

; covariance of pixels is denoted as

ξ_{e h}

; and

φ_{1}

φ_{2}

are used for stabilization.

A.PERFORMANCE ANALYSIS

The sample images processed in this proposed method for performing the image representation and restoration are shown in Fig. 2. The 6 images considered for the evaluation of MORSA-IDR are referred as $i m 1, i m 2, i m 3, i m 4, i m 5$ , and $i m 6$ .

Fig. 2. Sample blurred images.

These sample blurred images are processed under the proposed method to deblur the given input. For example, a $i m 6$ shown in Fig. 2 is processed, and the deblur output is obtained using the proposed method as shown in Fig. 3. The PSNR and SSIM of deblurred $i m 6$ are 30.98 dB and 0.93.

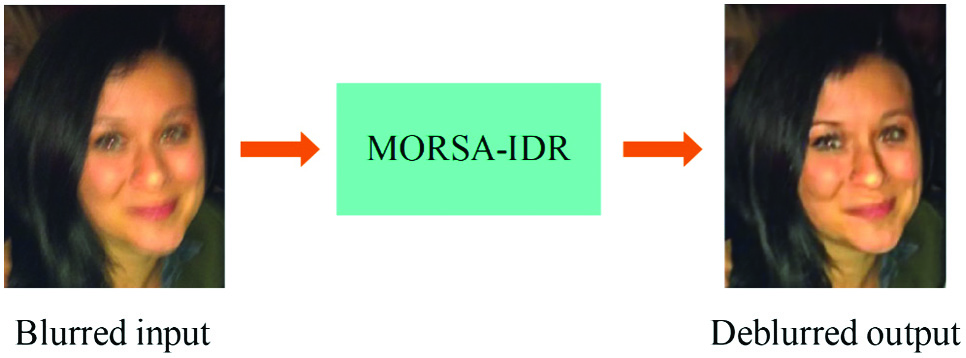Fig. 3. Restoration using proposed method.

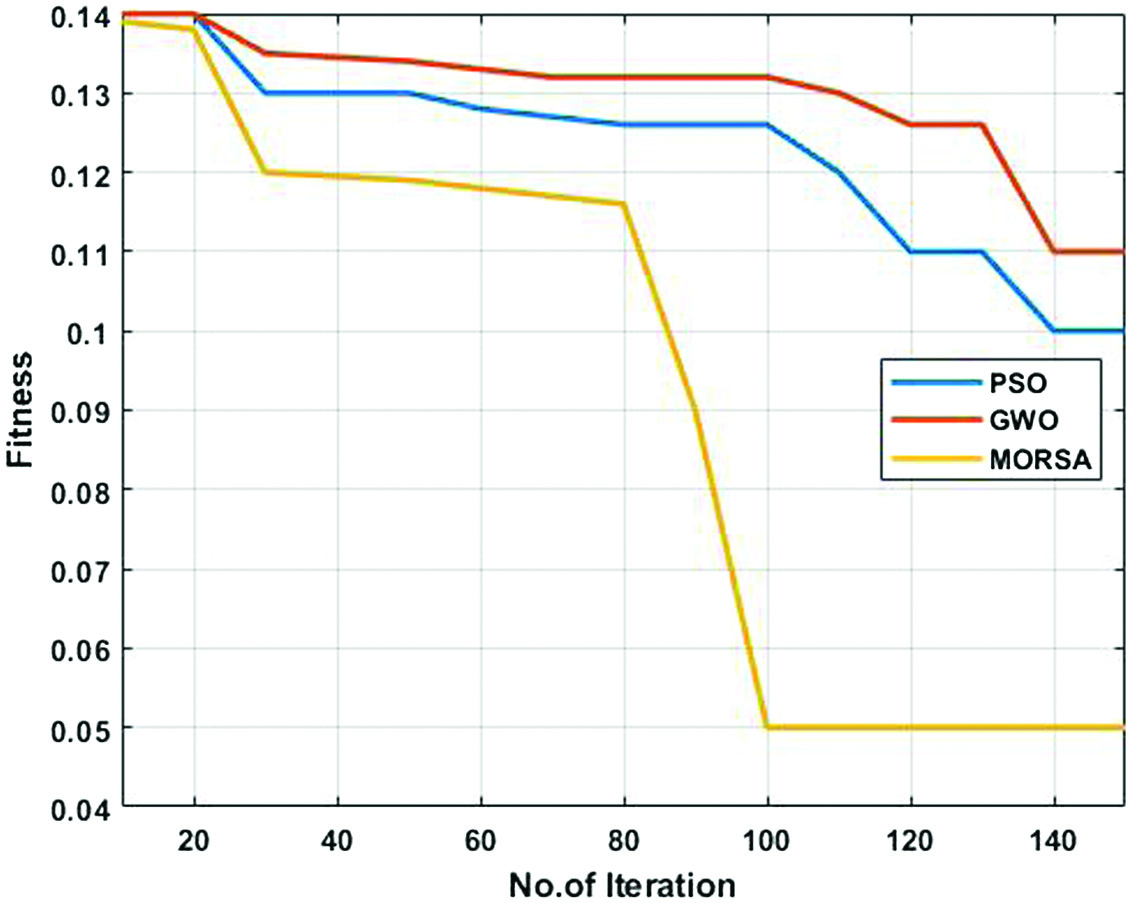
The fitness function graph for MORSA with different optimizations such as particle swarm optimization (PSO) and Grey wolf optimization (GWO) is shown in Fig. 4. The objective function considered for noise removal is used to converge the MORSA is faster than the PSO and GWO.

Fig. 4. Fitness function.

The PSNR is analyzed for different optimization and deblurring models as shown in Table II. Here, two different block sizes such as 3 × 3 and 5 × 5 are considered for analyzing the restoration performances. In that, different optimization includes particle swarm optimization (PSO) and Grey wolf optimization (GWO), whereas the different deblurring include convolutional neural network (CNN) and U-net. Further, PSNR comparison for different optimization methods is shown in Fig. 5. This analysis shows that the MORSA and proposed deblurring methods provide better performances than the other approaches. For example, the PSNR of MORSA for $i m 1$ is 31.021 dB, whereas PSO obtains 28.578 dB and GWO obtains 29.593 dB. The developed MORSA provides better performance than the PSO and GEO because of its effective equilibrium among the exploration and exploitation operations. Moreover, the kernel estimation computes new pixel for the noisy pixel of blurred image based on estimated threshold from MORSA. Accordingly, this kernel estimation is used to perform an effective deblurring of images which further helps to improve the PSNR.

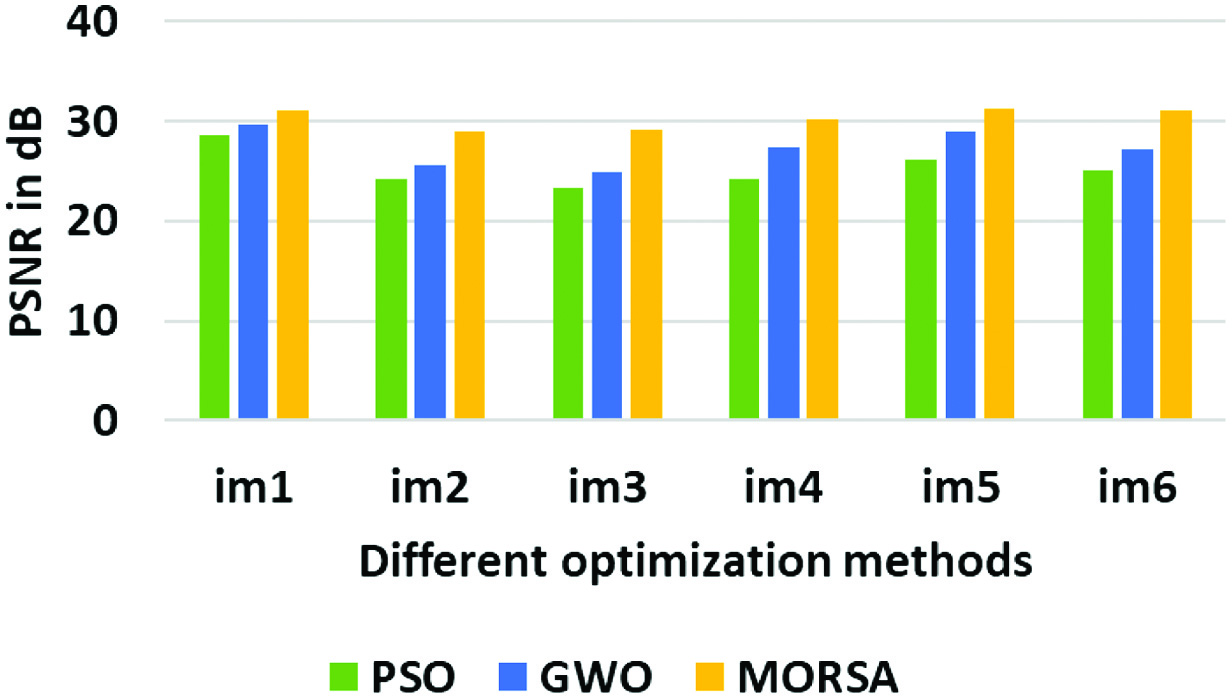Fig. 5. PSNR graph for different optimization methods.

Table II. PSNR analysis of proposed method

Block size	Images	PSNR (dB)
		Different optimization			Different deblurring methods
		PSO	GWO	MORSA	CNN	U-Net	Proposed
3 × 3	$i m 1$	28.578	29.593	31.021	30.002	28.615	31.021
	$i m 2$	24.113	25.600	28.947	26.204	24.810	28.947
	$i m 3$	23.281	24.918	29.081	28.892	27.080	29.081
	$i m 4$	24.200	27.399	30.114	28.575	26.656	30.114
	$i m 5$	26.082	28.984	31.215	29.963	29.040	31.215
	$i m 6$	25.082	27.128	30.988	29.236	28.520	30.988
5 × 5	$i m 1$	27.889	28.790	30.798	28.973	27.940	30.798
	$i m 2$	23.284	24.162	28.204	28.101	26.143	28.204
	$i m 3$	22.544	24.069	28.633	26.343	24.841	28.633
	$i m 4$	24.098	26.386	29.680	27.626	25.877	29.680
	$i m 5$	25.256	27.084	30.668	29.583	24.545	30.668
	$i m 6$	24.621	27.021	30.182	29.673	26.807	30.182

Similar to PSNR analysis, the SSIM also analyzed for different optimization and deblurring models as shown in Table III. Further, the graph for SSIM for different optimizations is shown in Fig. 6. From this analysis, it is found that the SSIM of proposed MORSA and deblurring model provides better performances than the PSO, GWO, CNN, and U-Net. For example, the SSIM of MORSA for $i m 1$ is 0.881, whereas PSO obtains 0.678 and GWO obtains 0.793. Since the searching operations of MORSA such as exploration and exploitation’s equilibrium result in optimal parameters of threshold and kernel. The MORSA achieves higher structural similarity because of effective identification of threshold and kernel parameters for deblurring and restoring the input images.

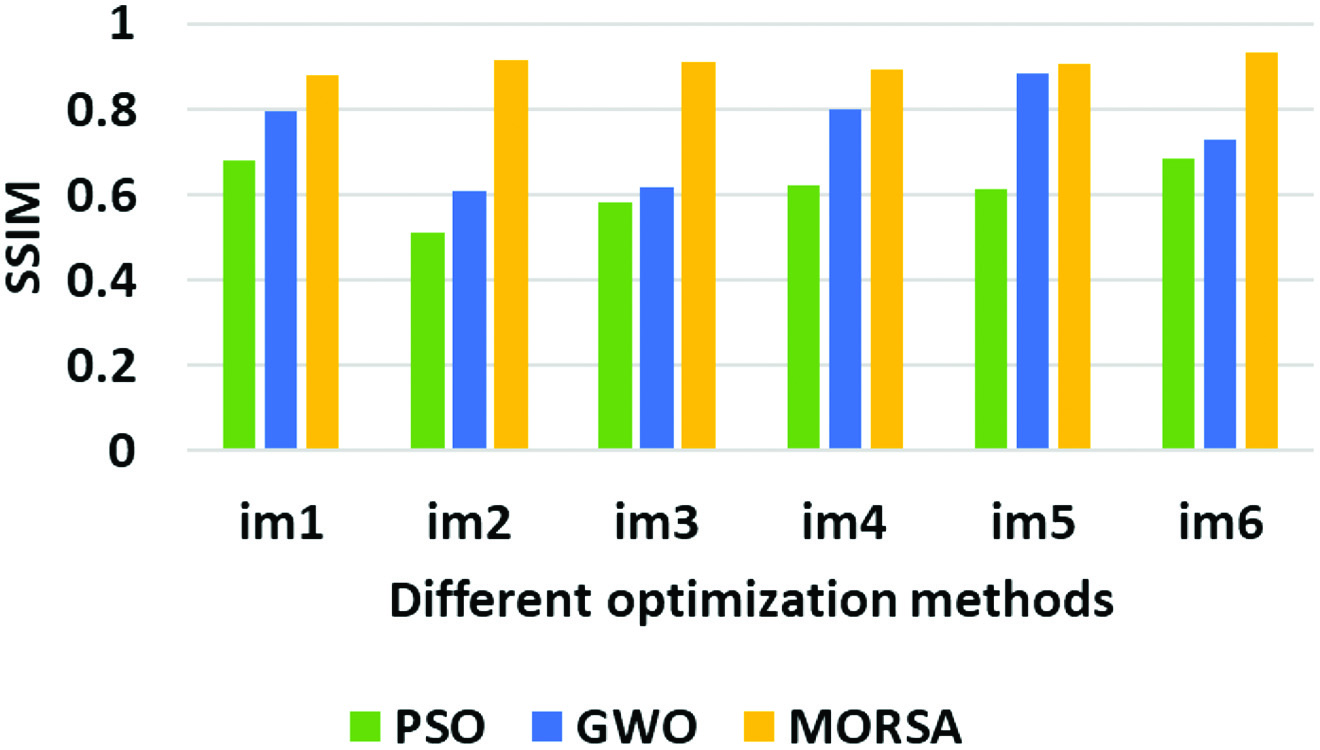Fig. 6. SSIM graph for different optimization methods.

Table III. SSIM analysis of the proposed method

Block size	Images	SSIM
		Different optimization			Different deblurring methods
		PSO	GWO	MORSA	CNN	U-Net	Proposed
3 × 3	$i m 1$	0.678	0.793	0.881	0.808	0.768	0.881
	$i m 2$	0.513	0.609	0.913	0.894	0.871	0.913
	$i m 3$	0.581	0.618	0.910	0.875	0.859	0.910
	$i m 4$	0.622	0.799	0.893	0.864	0.861	0.893
	$i m 5$	0.615	0.884	0.908	0.891	0.886	0.908
	$i m 6$	0.682	0.728	0.935	0.908	0.901	0.935
5 × 5	$i m 1$	0.667	0.766	0.834	0.794	0.683	0.834
	$i m 2$	0.492	0.601	0.905	0.788	0.725	0.905
	$i m 3$	0.558	0.611	0.909	0.879	0.822	0.909
	$i m 4$	0.609	0.781	0.885	0.771	0.734	0.885
	$i m 5$	0.608	0.880	0.899	0.804	0.768	0.899
	$i m 6$	0.678	0.719	0.921	0.907	0.884	0.921

The runtime, memory, and entropy analysis for different block sizes such as 3 × 3 and 5 × 5 are shown in Table IV. This analysis shows that the runtime for 3 × 3 block size is varied between 6.18s and 9.04s, whereas the 5 × 5 is varied between 6.34s and 9.11s. On the other hand, the memory used during the simulation is varied from 3.04KB to 5.88KB for 3 × 3, while memory of 3.81KB to 7.22KB is used for 5 × 5. Further, the entropy for 3 × 3 block size is varied between 6.44 and 7.58, whereas the 5 × 5 is varied between 5.97 and 6.84.

Table IV. Runtime, memory, and entropy analysis

Block size	Images	Runtime (s)	Memory (KB)	Entropy
3 × 3	$i m 1$	8.31	3.04	7.01
	$i m 2$	7.24	4.37	6.45
	$i m 3$	8.11	5.88	7.54
	$i m 4$	9.04	3.19	6.44
	$i m 5$	6.18	4.08	7.22
	$i m 6$	7.99	5.01	7.58
5 × 5	$i m 1$	8.64	3.84	6.84
	$i m 2$	7.29	5.01	6.27
	$i m 3$	8.31	7.22	6.18
	$i m 4$	9.11	3.81	5.97
	$i m 5$	6.34	6.01	6.37
	$i m 6$	8.08	5.22	6.09

B.COMPARATIVE ANALYSIS

Existing researches such as ELMI [19], DUBLID [20], and MAP [21] are used to compare the MORSA-IDR method. The ELMI [19], DUBLID [20], and MAP [21] have processed the $i m 6$ shown in Fig. 2, so the comparison is done for the same as shown in Table V. Further, the graphical illustration for the PSNR for MORSA-IDR with ELMI [19] and DUBLID [20] is shown in Fig. 7. This comparison depicts that the MORSA-IDR outperforms well than the ELMI [19], DUBLID [20], and MAP [21]. For example, the PSNR of MORSA-IDR for $i m 6$ is 30.98 dB, whereas the ELMI [19] obtains 30.45 dB and DUBLID [20] obtains 29.83 dB. The ELMI [19] and DUBLID [20] have to incorporate the noisy pixel discovery to further enhance the deblurring performances. Due to utilization of GPU, the runtime of DUBLID [20] is less when compared to the proposed MORSA-IDR. The main goal of the MORSA-IDR is to increase the PSNR and SSIM of restored images. So, the MORSA-IDR achieved high PSNR and SSIM with significant runtime when compared to the DUBLID [20]. The combination of noisy pixel discovery using DRN and kernel estimation along with MORSA help to enhance the deblurring and restoration performances.

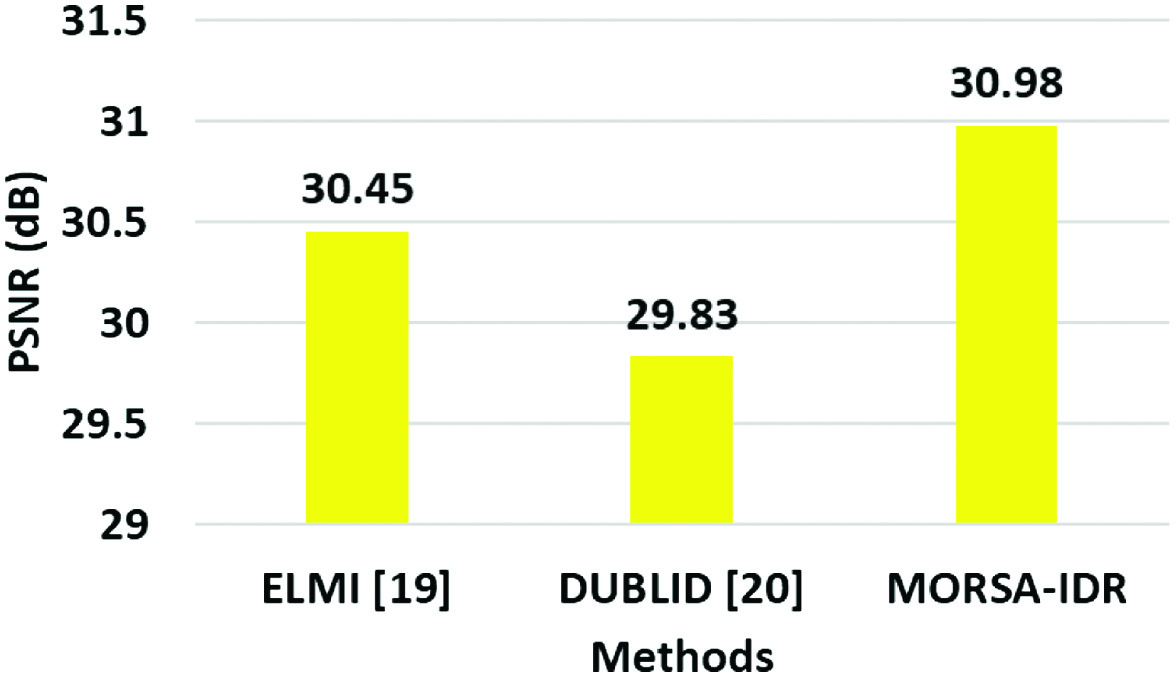Fig. 7. Graphical representation for the PSNR.

Table V. Comparative analysis for MORSA-IDR

Methods	PSNR (dB)	SSIM	Runtime (s)
ELMI [19]	30.45	0.921	NA
DUBLID [20]	29.83	0.892	0.08
MAP [21]	NA	NA	13
MORSA-IDR	30.98	0.935	7.99

V.DISCUSSION

This section provides the brief discussion about the results obtained from the MORSA-IDR to ensure the image deblurring and restoration. At first, the results of MORSA-IDR are compared with different optimization and deblurring models. The results show that the MORSA-IDR achieves the better PSNR and SSIM than the PSO, GWO, CNN, and U-Net approaches. For example, the PSNR of MORSA-IDR is 30.668 dB, which is high when compared with the PSO, GWO, CNN, and U-Net. Further, the MORSA-IDR is compared with the ELMI [19], DUBLID [20], and MAP [21] in comparative analysis section. The MORSA-IDR outperforms well than the ELMI [19], DUBLID [20], and MAP [21]. For example, the PSNR of MORSA-IDR for $i m 6$ is 30.98 dB, which is high than the ELMI [19] and DUBLID [20]. In this research, the DRN-based noisy pixel discovery and MORSA-based kernel estimation are used to enhance the image deblurring and restoration performances. The MORSA-IDR works well for unstructured and low light images during the image deblurring and restoration. However, if MORSA-IDR processed under highly unstructured images, it creates huge impact in the PSNR and SSIM measures.

VI.CONCLUSION

In this research, effective image deblurring and restoration are achieved based on the detection and replacement of noisy pixel and image deblurring processes. Initially, the DRN is used for discovering the noisy pixel from the input, and the statistical model is used for removing the noisy pixel. The optimal threshold values for the statistical model are identified using the MORSA, which resulted in the calculation of new pixels for noisy pixels. Later, kernel estimation along with MORSA was developed for enhancing the image deblurring process. Therefore, the low-level contextual data from the corrupted image are acquired by using the developed MORSA-IDR method. The outcomes of MORSA-IDR show that it outperforms well than ELMI and DUBLID. The PSNR of MORSA-IDR for image 6 is 30.98 dB, which is high when compared to the ELMI and DUBLID. In the future, the novel optimization algorithm can be used for improving the deblurring performances under highly unstructured images.

Multiobjective Reptile Search Algorithm Based Effective Image Deblurring and Restoration

I.INTRODUCTION

II.RELATED WORK

III.PROPOSED METHOD

A.DATA ACQUISITION AND DISCOVERY OF NOISY PIXELS USING DRN

B.STATISTICAL MODEL-BASED NOISE REMOVAL

C.THRESHOLD CALCULATION FOR NOISE REMOVAL USING MORSA

1)ITERATIVE PROCESS OF MORSA

2)OBJECTIVE FUNCTION OF MORSA FOR NOISE REMOVAL

D.KERNEL ESTIMATION-BASED IMAGE DEBLURRING

E.OBJECTIVE FUNCTION FOR KERNEL ESTIMATION

IV.RESULTS AND DISCUSSION

A.PERFORMANCE ANALYSIS

B.COMPARATIVE ANALYSIS

V.DISCUSSION

VI.CONCLUSION

References