JAIT

I.INTRODUCTION

A feature of ground-based mobile walking robots is the discreteness of the interaction of the propulsion device with the ground. The phase of interaction with the supporting surface in which the traction properties of the propulsion device are realized is distinguished, and the transport phase in which the foot of the propulsion device moves in space and takes a new position on the ground. This movement includes lifting the foot above the ground and moving it to a new position in the course direction. For ground-based mobile walking robots, variants of solving the problem of transferring stop walking mechanisms are known. For example, a modified stop transfer path [1] is known, proposed in the absence of sufficient information about the surface profile, or the equation for the optimal raising and lowering of the foot of an orthogonal propulsion device [2] if such information is available. Moreover, the optimality criteria can be different and additively include indicators differing in their significance, such as, for example, the level of heat loss in the engines, the force developed by the drives, the transfer time, in general, and the raising and lowering of the foot, in particular [3].

A feature of walking robots moving along the bottom of a reservoir is:

–the presence of buoyancy forces affecting the forces of interaction of the propulsion device with the ground;
–a higher force of resistance to movement of the robot as a whole, and of the transported mover due to their movement in a denser environment;
–possible undercurrents that affect the transported propulsion device in an arbitrary direction; and
–additional resistance force acting on the foot of the mover when it is separated from the bottom during the rise [4], [5], due to the adsorption of gases dissolved in water and slow filtration of the liquid in the soil [6], [7].

The latter leads to the so-called compression effect, which consists in the fact that there is a significant force that impedes the shear and tearing of the propulsion device support from the bottom soil. The need to overcome this additional force leads to increased energy costs for the movement of the robot, and in some cases can lead to a stop of the robot and its further immersion in the bottom soil. Overcoming the negative consequences of the “compression” effect can go in different directions: improving the construction of supports, introducing additional mechanisms that violate the conditions for this effect to occur, as well as constructing such laws for controlling the movement of the support of a walking propulsion device that would provide a minimum of energy for lifting, a minimum of forces developed by the drive, or other performance indicators, or a comprehensive criterion that takes into account part or all of the possible quality indicators. The lifting of the foot can be carried out in accordance with various laws of the drive of its vertical movement. In this case, the force, power, heat loss level, and other characteristics of the lifting process developed by the drive will depend on the selected law, and you can find the conditions under which the movement will occur with the best indicators from the point of view of the researcher.

Thus, to select a drive that provides a foot lift for walking robots developed at the Volgograd State Technical University [8], [9], it is necessary to establish patterns that ensure the optimal movement..

II.FORMULATION OF THE PROBLEM

A horizontal plate of mass m and area S translationally moving along the vertical axis in a liquid medium with a known permeability coefficient k and dynamic viscosity μ is considered as a design scheme for the foot of a walking propulsion device interacting with soil of the bottom of a reservoir (Fig. 1).

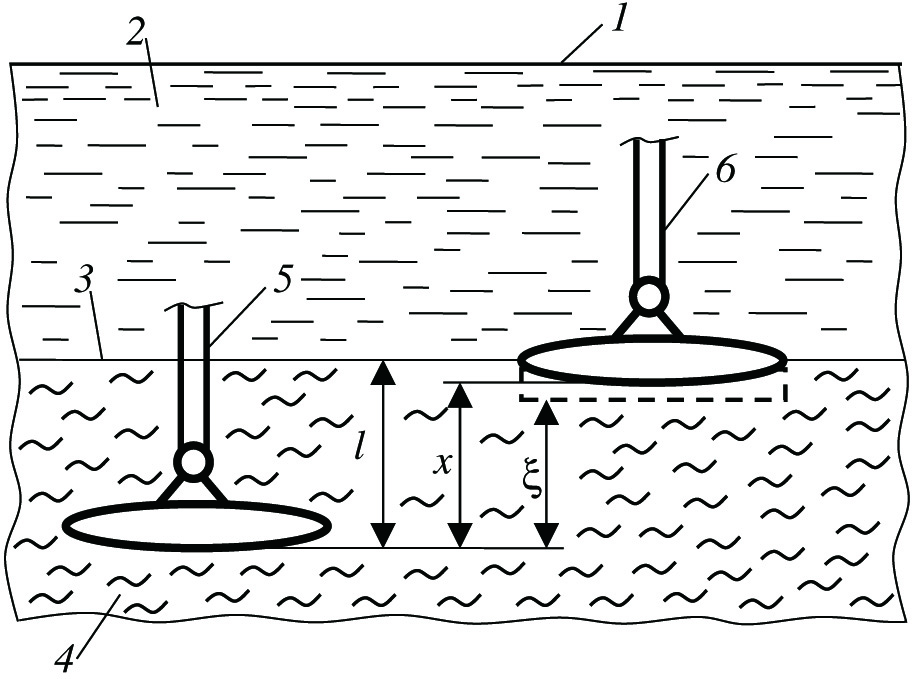Fig. 1. Design scheme of the propulsion device immersed in the ground: 1, the surface of the reservoir; 2, the reservoir; 3, the boundary of the reservoir and the bottom soil; 4, bottom soil; 5, the support stand of the propulsion device; and 6, foot propulsion device.

At the stage of traction mode, the plate is at rest, and at the stage of lifting, forces act on it: mg, the weight of the plate; T, the force developed by the drive lifting the foot of the propulsion device; and P₀S, PS, respectively, the pressure force of the water on the lower and upper surface of the plate. In equilibrium P = P_∗

P_{*} S - P_{0} S = F,

(1)

where F is the buoyancy force.

When the plate moves immersed in the soil upward, a vacuum forms under it, due to the expansion of the volume of dissolved air in the liquid in accordance with Henry’s law [10]. In the calculation scheme, this is taken into account by the difference in coordinates between the bottom surface of the plate x and the surface of the liquid ξ

Δ = x - ξ .

(2)

In the equilibrium position of the foot at t = 0

ξ_{0} = - Δ_{0}, x_{0} = 0, {\dot{x}}_{0} = 0, {\dot{ξ}}_{0} = 0 .

(3)

The rise of the foot is carried out with an initial zero speed under the action of the force T developed by the lift drive. When the foot reaches the height x = l_∗, the foot comes off the ground and the force caused by the “compression” under its lower base ceases to act on it.

The equations of motion of the foot when it is separated from the ground are compiled on the basis of Henry’s law [10], the law of gas expansion during the polytropic process, Darcy’s law on fluid filtration [6], and the theorem on the motion of the center of mass of a solid [11].

Henry’s law, on the concentration of gas in a liquid medium, which is expressed in the introduction into the design model of the height Δ₀ of the gas column under the base plate.

The law of gas expansion in the polytropic process and the rise of the foot

P (x - ξ)^{n} = (P_{0} + \frac{F}{S}) Δ_{0}^{n},

(4)

where n is the polytropic index.

With a relatively slow rise and heat exchange, which ensures a constant temperature, n = 1.

Darcy’s law of liquid filtration

\frac{d ξ}{d t} = α (P_{0} + \frac{F}{S} - P), α = \frac{k}{μ L},

(5)

where k is the coefficient of soil permeability, μ is the dynamic viscosity of the liquid, and l is the conditional height of the column of bottom soil through which filtration occurs.

For the foot of a walking propulsion device, the conditional height of the filtration column l is the most difficult to determine. It is permissible to assume that as the foot rises in the ground, the filtration column decreases, and reaches its maximum value when the foot is stationary, which perceives the load G from the weight of the robot.

l_{*} = \frac{G}{S c},

(6)

where c is the coefficient of volumetric crumpling of the bottom soil.

In real conditions α, it should be determined experimentally, and in the design scheme it is considered a constant value.

Theorem on the motion of the center of mass of a solid body in the absence of a normal ground reaction

m \ddot{x} = - m g + T - P_{0} S + P S .

(7)

Equations (4 –7) are reduced to two jointly solvable equations

{\begin{cases} \dot{ξ} = α (P_{0} + \frac{F}{S}) (1 - \frac{Δ_{0}}{x - ξ}), \\ m \ddot{x} = T - m g + F \frac{Δ_{0}}{x - ξ} + P_{0} S \frac{Δ_{0} + ξ - x}{x - ξ} . \end{cases}

(8)

Equation (8) is a system of two nonlinear differential equations with respect to variables x(t) and ξ(t). The initial conditions for the variables are established from (3).

The system of differential (8) can be solved by numerical methods. However, this can only create the appearance of an exact solution due to the approximate determination of the parameters α and Δ₀.

Moreover, the numerical solution does not allow obtaining a clear analytical idea of the influence of various parameters of the system under consideration on the nature of the process under study. A numerical solution, according to the authors, is necessary when solving a specific engineering problem aimed at developing a specific technical system.

Usually one of the well-known methods is used: the method of a small parameter inherent in the works of A. Poincaré [12], [13], the Krylov-Bogolyubov method [14 ]–[16], and so on.

Therefore, it is advisable to linearize (8), assuming that x−ξ−Δ₀ it is small.

Then, instead of (8), there are linearized equations admitting an analytical solution

{\begin{cases} \dot{ξ} = α (P_{0} + \frac{F}{S}) \frac{x - ξ - Δ_{0}}{Δ_{0}} \\ m \ddot{x} = T - m g + F - (P_{0} S + F) (\frac{x - ξ}{Δ_{0}} - 1) . \end{cases}

(9)

Equations (9) can be reduced to a single differential equation. To do this, from the first (9), we express

x = ξ + \frac{\dot{ξ} Δ_{0}}{α (P_{0} + \frac{F}{S})} + Δ_{0},

(10)

and substituted into the second equation.

As a result, there is a linear differential equation [17], [18] of the third order with respect to ξ or of the second order with respect to $\dot{ξ} = V$

\frac{m Δ_{0} S}{α (P_{0} S + F)} \ddot{V} + m \dot{V} + \frac{S}{α} V + m g - F = T, α = \frac{k}{μ L}, V = \dot{x} - \dot{Δ},

(11)

where k is the soil permeability experimentally determined coefficient, μ is the dynamic viscosity of the liquid, L is the conditional height of the bottom soil column through which the filtration occurs, and x is the vertical coordinate of the foot.

Due to the alleged smallness in (11), the foot speed is understood, which is provided by the drive of its vertical movement.

Thus, the task is to determine such a law of vertical movement of the foot, for a given time, which ensures a minimum of heat loss in the drive motor. Heat losses [19] are determined by the integral

W = ν \int_{0}^{τ} T^{2} d t

(12)

where ν is the constant of the engine.

III.SOLUTION METHOD

We consider a method for ensuring the minimum integral (12) based on the application of the Euler–Poisson equation with the involvement of an isoperimetric condition for the passage of distance l_∗ in time τ [20].

To create Euler–Poisson equations, the functional (12) should be combined with a functional that characterizes the isoperimetric condition

\int_{0}^{τ} V d t = l_{*} .

(13)

Then the combined integrand function with an indeterminate factor η has the form

Φ = ν T^{2} + η V,

(14)

with respect to which the Euler–Poisson equation is compiled

\frac{d^{2}}{d t^{2}} (\frac{\partial Φ}{\partial \ddot{V}}) - \frac{d}{d t} (\frac{\partial Φ}{\partial \dot{V}}) + \frac{\partial Φ}{\partial V} = 0.

(15)

In view of (11) and (14), (15) has the form

\begin{array}{l} {[\frac{m Δ_{0} S}{α (P_{0} S + F)}]}^{2} \overset{ṫ}{V} + \\ + [\frac{2 m Δ_{0} S^{2}}{α^{2} (P_{0} S + F)} - m^{2}] \ddot{V} + \\ + \frac{S^{2}}{α^{2}} V + \frac{2 S}{α} (m g - F) + \frac{η}{ν} = 0. \end{array}

(16)

Equation (16) is a linear, inhomogeneous differential equation of the fourth order. Its solution is known and depends on an indefinite constant η. To determine it, (13) should be solved taking into account V = V(η,t).

However, to solve the problem of controlling the rise of the foot, it is necessary to determine arbitrary integration constants, and for this to adequately choose the boundary conditions if t = 0, it is obvious that V = 0 the other three conditions can be different.

Table I schematically presents the possibilities for implementing 35 different boundary conditions. In the particular case, they can be initial for the Cauchy problem.

Table I. The Possibilities for Implementing 35 Different Boundary Conditions

	V_n
t	$\overset{}{V}$	$\dot{V}$	$\ddot{V}$	$\overset{ṫ}{V}$
t = 0	V₀ = 0	${\dot{V}}_{0}$	${\ddot{V}}_{0}$	${\overset{ṫ}{V}}_{0}$
t = τ	V_τ	${\dot{V}}_{τ}$	${\ddot{V}}_{τ}$	${\overset{ṫ}{V}}_{τ}$

From 35 variants of the allowed boundary conditions from Table I, one should choose three corresponding to the task.

One of the solutions of (16), provided that at t = 0

\begin{array}{l} V = 0, \\ \dot{V} (0) = - n u, \\ \ddot{V} (0) = (n^{2} - ω^{2}) u, \\ \overset{ṫ}{V} (0) = (3 ω^{2} - n^{2}) u, \\ u = \frac{2 α}{S} (m g - F) + \frac{η}{ν} \frac{α^{2}}{S^{2}}, \end{array}

(17)

have the form

V = u (1 - e^{- n t} cos ω t),

(18)

where n, ω are defined from the system of equations

{\begin{cases} ω^{2} - n = \frac{B}{2 A}, \\ ω^{2} n^{2} = \frac{4 A C - B^{2}}{16 A^{2}}, \\ A = {[\frac{m Δ_{0} S}{α (P_{0} S + F)}]}^{2}, \\ B = \frac{2 m Δ_{0} S^{2}}{α^{2} (P_{0} S + F)} - m^{2}, \\ C = \frac{S^{2}}{α^{2}} . \end{cases}

(19)

The graphs (Fig. 2) show the dependences of speed and coordinates at the optimal mode of lifting the foot to a height l_∗ = 0.2 m and in accordance with the law

V = u (1 - e^{- n t}),

(20)

where n = 10 s⁻¹, u = 0.36 m/s, m = 40 kg, Δ₀ = 10⁻³ m, S =10⁻⁴ m², α = 5 × 10⁻⁸ m²s/kg, P₀ = 2 × 10⁵ Pa, and F = 50 N.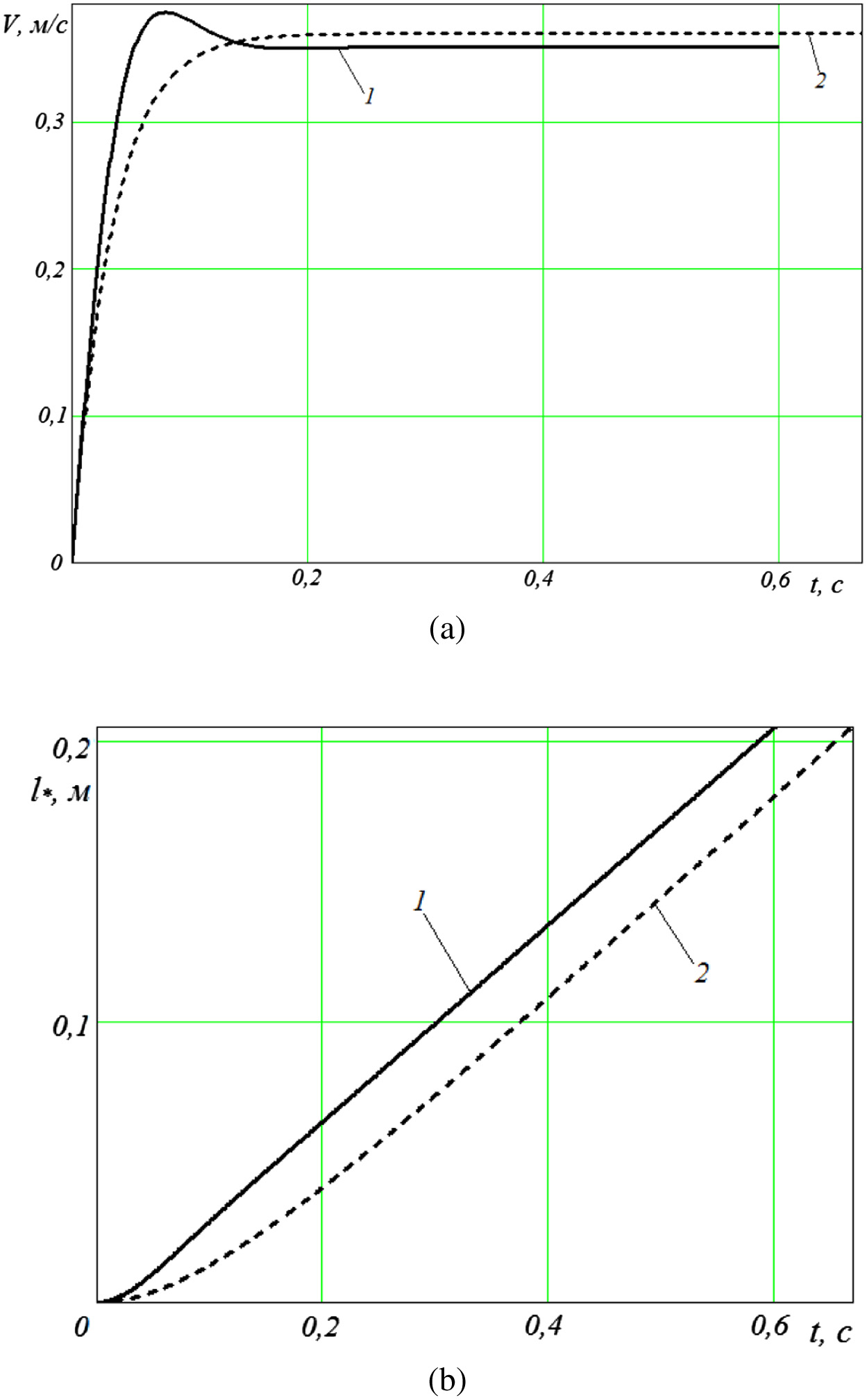

Fig. 2. Dependence of (a) speed and (b) coordinate with the optimal mode providing a minimum of heat losses W (12) of lifting the foot: 1, optimal mode; 2, not optimal mode.

An analysis of the results shows that the nature of the optimal modes of motion differs from the previously obtained laws of motion [17], and the energy-optimal mode by the criterion of heat loss exceeds the nonoptimal one by 5%.

IV.CONCLUSIONS

A method for determining the optimal motion modes, from the point of view of minimum heat loss in the lifting drive of the walking propulsion device, taking into account the additional force acting on the foot due to the “compression” effect is proposed [21]. It is shown that due to the optimal control of the movement of the support of the walking propulsion device, it is possible to achieve a reduction in energy losses due to resistance to the forces moving under water. This is because the description of the physical nature of the processes that occur allows us to find ways to solve the problem of using them for the good. In the future, it is planned to build a laboratory model for studying the movement of a walking propulsion device under water and in interaction with bottom soil to verify and adjust the mathematical models proposed in this work.

On Determining the Optimal Lifting Law of the Walking Propulsion Device Foot of an Underwater Robot from the Bottom

I.INTRODUCTION

II.FORMULATION OF THE PROBLEM

III.SOLUTION METHOD

IV.CONCLUSIONS

ACKNOWLEDGMENTS

REFERENCES