I.Introduction
The increasing number of human-made satellites in low earth orbit (LEO) [1] creates difficulties for astronomical observations surveying large sections of the sky, as well as observations with long exposure times [2]. For such observations, man-made satellites can create artifacts such as streaks when satellites move across the observation’s field of view, as shown in Fig. 1. These streaks are caused by sunlight reflecting off the satellite and back towards the ground, resulting in a brightness, or apparent magnitude (m), that is much higher than the objects under observation. This saturates measurements in locations that the streak covers, rendering that data unrecoverable and introducing an artifact that can affect downstream analysis.
Fig. 1. An observation containing a satellite streak from the Trailblazer [3] repository. This image is characteristic of real-world observations, with embedded stars (black) and background noise (gray).
As established at the SATCON1 workshop [4] by NSF’s NOIRLab and the American Astronautical Society, the effects of these artifacts on downstream scientific analysis can be significant. For example, the relatively bright streaks caused by satellites can confuse automated processing pipelines that are designed to identify stellar objects, resulting in erroneous downstream data. They can also result in decreased efficiency, as multiple observations may now be necessary where only one was previously, and decreased overall effectiveness as important data may be covered up by the streak of a transient satellite [4].
A number of detection algorithms have been developed to filter this compromised data. Traditional algorithms have had some success, which can be improved when multiple exposures of the same region of sky are combined [5] or when known locations of stars are considered. Another approach is to use precise tracking data to calculate where and when an object in LEO should cross the field of view of the observation and then proactively ignore data from those pixels at those times [6]. These approaches require additional information and data to be collected, which may not always be available or accurate.
Machine learning provides an alternative to traditional filtering methods that can function on single observations with no other assistance while also supporting efficient scalability. This is possible because of advancements in the efficiency and capability of deep learning-based models through the extraction of features using pre-trained general models and then utilizing specially trained models to segment the desired features (e.g., [7]). One such model that follows this approach is U-Net [8] which is commonly used as the basis for many deep learning models, especially in medical imaging.
This paper proposes a deep learning model based on the existing U-Net platform that detects and masks out pixels in an observation determined to have been affected by the streak of a satellite or other LEO object. We show that this model, as an example of machine learning, is both significantly more accurate than traditional non-ML methods and is faster to execute. To compare our method more accurately with existing techniques, we also propose a novel metric, the Star Occlusion Factor (SOF), to evaluate data loss caused by masking pixels containing scientifically useful data. The research objectives of our work are:
RO1: Evaluate the effectiveness of a common medical-grade machine learning model and its suitability for use in filtering satellite streaks.
- RO1.1: Perform a quantitative evaluation of the computing efficiency of the proposed machine learning model in comparison with existing methods.
- RO1.2: Perform both quantitative and qualitative evaluation of the errors made by the proposed model in comparison with errors made by existing methods.
The rest of the paper is structured as follows: Section II presents the related work. Section III describes the data management processes used, the traditional methods, as well as the design of the ML model. Section IV presents the results achieved. Section V discusses the results and compares qualitative aspects of each method, and lastly, Section VI summarizes our contributions and conclusions.
II.RELATED WORK
Data management is an essential part of the astronomical process. As data quantities increase, especially with the advent of whole sky surveys which can generate terabytes of data in days [9], it is infeasible for incoming data to be processed manually. Therefore, the need for automated data processing and cleaning pipelines is greater than ever. Efforts to manage this flow of data have covered many different areas, from enabling efficient distribution and replication of the data [10] to automated labeling and categorization of the objects being imaged [11]. There is also significant interest in denoising and general cleaning of the data before it is analyzed (e.g., [12]).
Previous work in astronomical image denoising has focused on traditional algorithmic approaches for the detection and masking of streaks. Pyradon [13] is a tool suite for the detection and masking of satellite streaks utilizing a Radon transform mechanism. It exploits the fact that satellite streaks are typically straight and detects linear artifacts in supplied images. Pyradon also contains a set of tools for generating representative simulated datasets of astronomic samples containing satellite streaks. Some features that improve the representativeness of the generated samples include the use of a Point Spread Function that distorts light sources in the same way that the optics of a real telescope would, and the addition of Gaussian noise to simulate the background noise. ASTRiDE [14] is a tool for the detection of mostly linear artifacts in astronomic images. It utilizes boundary tracing to find the outline of all objects in the image and then filters down to only boundaries that are mostly linear in nature. Its primary use case is for the detection of unknown moving objects in LEO [15]. Some alternative approaches have also been proposed, such as performing analysis on spectrogram data rather than directly on optical data [16], with some success in higher noise environments.
Some initial ML approaches for streak detection have been developed; however, they have significant limitations. DeepStreaks [17] is a toolset for the detection of linear streak artifacts caused by objects in LEO. It uses several CNN models to detect and classify streaks in supplied images. However, since it does not generate data for the geometry of the streak, it cannot generate pixel masks of the detected streak.
Recent advances have been made in ML models capable of classifying individual pixels of an image as belonging to an object or not (image segmentation). One such model architecture is U-Net [8], which utilizes a multi-step approach of multiple convolutional neural networks (CNNs) chained together, combined with a series of upscaling networks to achieve high levels of effectiveness and efficiency for general-purpose image segmentation tasks. For example, it has been applied to road extraction [18], identification of buildings from satellite imagery [19], and identification of microorganisms [20]. U-Net was originally developed for medical image segmentation [21], but has already seen some use for the mitigation of artifacts in radio astrometric data [22].
CNNs reduce the pixel array of an image into a smaller array that describes the features contained in that image. The benefit of this approach is that less data are required to describe the image, and thus, it is more efficient to process. A CNN does this through a kernel describing how neighboring pixels affect a region as it is mapped onto the smaller convolved array. It then has a pooling layer that functions as a denoiser and either takes the maximum, or average, value found in a region of the convolved array and projects it into a smaller pooling array [23].
CNNs have also been applied in detection applications for particle streaks [24], both for boundary box generation as well as masking of streaks. This demonstrates the ability of CNNs to identify and mask a single streak even when noise and other artifacts are present in the proximity of the desired streak.
Another reason for the potential suitability of CNNs for this application is their exceptional performance in denoising applications [25]. Indeed, CNNs have been applied to the problem of denoising astronomical data so that further analysis can be performed more easily [26]. Several architectures have been used for this purpose, including U-Net [27]. CNNs in these kinds of applications consistently demonstrate improved efficiency when compared to traditional methods.
III.METHODS
A.DATASET
To evaluate our method, we constructed a data-driven workflow in Python to reproducibly generate a dataset utilizing Pyradon’s simulation tool and perform our later evaluation. Training datasets that utilize generated data is a rising practice (e.g., [16,24,26]) and allows development of models even when real-world labeled training data is sparse or unavailable. The principle of domain randomization [28] allows our synthetic data to generalize to real-world data. Fig. 2 is an overview of our process for generating the dataset.
Fig. 2. Workflow for generating our dataset. During execution, several output image variants are saved for later analysis and processing.
The dataset consists of 256 × 256 pixel images managed with NumPy [29], containing between 0 and 25 stars of varying brightness in random positions, distributed uniformly. Brightness varies evenly between fully dark and fully bright. Gaussian noise is added to the image in order to simulate sensor noise characteristically found in real-world observations (see [30]). A global predefined seed is used in order to ensure run-to-run consistency of generated noise while preserving randomization of stars between samples. Lastly, a simulated streak is added to each image with varying length, origin, and intensity to form the final image (e.g., Fig. 3). This image is representative of a standard single capture which contains stars of varying intensity as well as a transient high apparent magnitude object such as a satellite. A binary pixel mask of the streak itself is saved alongside the image (e.g., Fig. 4) and later serves as ground truth for evaluation. All pixels which contain a streak in Fig. 3 are marked as true (white), while pixels that do not contain part of a streak are marked false (black). Variants of the images without a streak are also saved for use during performance analysis as well as metadata about the location and brightness of the streak. This approach is used to generate ten thousand samples in order to adequately characterize the degrees of freedom for the streak: origin, rotation, length, and brightness. Following convention [30], 80% of the dataset is used for training and the remaining 20% is held back for evaluation.
Fig. 3. A generated image. As in real-world images, it contains a streak, stars, and background noise.
Fig. 4. Baseline streak mask. White pixels contain part of a streak.
B.TRADITIONAL ALGORITHMS
We evaluated the performance of two approaches that use traditional algorithms, Pyradon and ASTRiDE, to provide context for our ML approach. For our evaluation, we apply each of the three approaches to the testing portion of the dataset (which contains sample images with streaks) and then process their respective results to compute masks such as shown in Fig 4. Once the output tools are unified into pixel masks, they can be fairly compared using the same metrics.
We first used one of Pyradon’s utilities to perform streak detection. It takes in a grayscale image, utilizes a radon transform to locate streaks in the image, and then generates metadata for each found streak including position, rotation, and length. The equation for the Radon transform used by Pyradon is given in Equation (1) [13], where R is the resulting transform, is the starting coordinate of the line, is the horizontal run of the line, and is the total height of the image. Using and we are able to conceptualize the slope of the line, and keeping the second axis as allows the resulting transform to remain discrete and pixel-based rather than continuous as an angle. The specific algorithm utilized by Pyradon is a Fast Radon Transform, which uses dynamic programming to reduce redundant calculations in order to improve efficiency by several orders of magnitude. This is possible because of the discrete pixel nature of digital images. It can use this information to generate a mask of all pixels affected by the streak, which we save for analysis and comparison to the ground truth.
ASTRiDE’s streak detection was performed using ASTRiDE’s built-in streak detector. The detector functions by implementing boundary detection to trace the outline of all distinct objects in the image. This is done using scikit-image’s [31] find_contours, which in turn uses a variant of the Marching Cubes [32] algorithm called Marching Squares to find the contours. A filter is then applied to all of the detected objects based on their outline’s shape. Each shape is assigned a score according to how similar it is to a circle. For example, a circular object would score close to 1, a square object would score 0.78, and a long thread-like object would score close to 0. Outlines with a score higher than a threshold are then removed from consideration. The default threshold value of 0.2 was used. The output of the streak detector is a list of contours, or outlines, of all streaks detected. These contours must be converted into a pixel image in order to apply the same pixel-based evaluation method necessitated by the other approaches. We used scikit-image to construct a polygon of the enclosed area. We then converted the polygon to a binary pixel mask of all affected pixels and saved it for analysis and comparison to the ground truth.
C.MACHINE LEARNING APPROACH
We constructed a neural network based on the U-Net architecture and the needs of our domain. U-Net stacks CNN layers in order to efficiently extract feature information from an image (the encoder stage) and classifies pixels belonging to the desired feature (the decoder stage). U-Net is highly effective at generic image segmentation tasks (e.g., [15]). For the encoder, we used MobileNetV2 which is a robust and efficient CNN encoder for general-purpose image segmentation [33]. For the decoder, we used 4 layers of pi × 2pi× [34] to perform upscaling and image segmentation due to its suitability for general-purpose uses. The encoding stage model is pre-trained, and we trained the decoding stage specifically for our application.
To train our system, we used 8000 samples from the dataset generated using Pyradon. Training was performed over 20 epochs, using the Adam optimizer and the Sparse Categorical Cross-entropy loss function from Keras [35]. To ensure rapid training for iterative development of the ML model, the images as well as associated masks were downscaled to 128 × 128 pixels from their original size. Downscaling in this manner is a common strategy to improve training speed and effectiveness (e.g., [24,36]). The trained ML model was used to generate streak masks for the 2000 sample validation set. As traditional approaches, the training data were not used by the other approaches. The computed masks were then upscaled from their 128 × 128 native resolution to the standard 256 × 256 resolution using Nearest Neighbor interpolation. Like all approaches, this mask was saved for evaluation.
The execution time of each approach was measured using Python’s time module and excluded the time to load the dataset into memory. Testing was performed on an Intel Core i7-12700H running at 4.14 GHz with an Nvidia RTX 3050ti GPU. Pyradon and ASTRiDE are CPU-bound approaches, while our machine learning model can leverage the GPU. The consumer nature of this hardware (i.e., not requiring highly specialized equipment) demonstrates the performance advantage and applicability of our work.
D.METRICS
Several standard metrics were used to evaluate the performance of each method tested. Initially, mean squared error (MSE) and mean absolute error (MAE) were used as baseline statistical metrics. As a more domain-appropriate measure, Intersection over Union (IoU) [37] was also applied. IoU is an error metric commonly used to evaluate the performance of image segmentation solutions. It is calculated by dividing the number of pixels in the intersection of the predicted mask and the ground truth mask and dividing by the union of all pixels in the predicted and ground truth masks. In the resulting score, a score of 1 represents perfect overlap, and a score of 0 represents no overlap between the predicted mask and the ground truth mask. The definition for IoU [37] is given in Equation (2), where A is the set of pixels in the ground truth mask and B is similarly extracted from the generated mask being evaluated.
However, none of these metrics are ideal for this problem domain because they treat all non-streak pixels as having the same scientific value regardless of what data they contain. Some pixels will contain data, such as stars, which is more useful than other pixels that contain only noise. There is also a potential for some methods of generating streak masks to erroneously include pixels containing stars because of their relatively high brightness value. This can have a negative impact on downstream analysis, such as star cataloging (e.g., [38]). A metric that can express this tendency can improve the accuracy of solution analysis for this problem.
Therefore, we propose a new metric for this domain, the SOF. SOF is designed specifically to evaluate the exclusion of target data in astronomic processing. SOF is calculated by dividing the number of pixels containing stars that have been masked by the total number of pixels containing stars present. The definition for SOF is given in Equation (3) where S is the set of pixels containing one or more stars and B is the set of pixels in the streak mask being evaluated.
This formulation is made possible by the use of generated data which includes ground truth data indicating the position and size of stars. In effect, SOF is a measurement of how much useful data are being excluded by the generated masks. Two variants of SOF were implemented: SOFa in which all stars in the frame are considered for the metric and SOFb which excludes stars containing pixels that have been covered by a streak from consideration. The former variant is an expression of the total data loss, while the second variant expresses only the data which were lost unnecessarily.
IV.EXPERIMENTAL RESULTS
Each approach was evaluated on 2000 samples derived from the Pyradon dataset. These samples were distinct from our ML model’s training set. Generated masks for each method were collected (representing the ground truth from Pyradon) and compared to the true mask for each sample. MSE and MAE for the number of incorrect pixels in each mask were calculated for each method, as well as the average IoU. These results are shown in Table I. Average SOFa and SOFb were also calculated and are shown in Table II.
Table I. Error values for tested methods
| Method | MSE | MAE | IoU |
|---|---|---|---|
| ML | 10262.474 | 0.003145 | 0.803 |
| ASTRiDE | 516299.0805 | 0.008157 | 0.514 |
| Pyradon | 2494471.283 | 0.020974 | 0.431 |
Table II. Star Occlusion Factor values for tested methods and ground truth
| Method | Average SOFa: including streak stars (%) | Average SOFb: excluding streak stars (%) |
|---|---|---|
| ML | 9.25 | 1.50 |
| ASTRiDE | 6.34 | 1.07 |
| Pyradon | 12.98 | 7.17 |
| Ground Truth | 9.27 | 0.00 |
ASTRiDE has a tendency to omit the generation of a mask entirely in certain situations, making its score vacuously low.
Rates for true positives (TP), true negatives (TN), false positives (FP), and false negatives (FN) were calculated for each method in order to create a confusion matrix. Figures 5–7 contain the calculated confusion matrix for the ML model, ASTRiDE, and Pyradon, respectively.
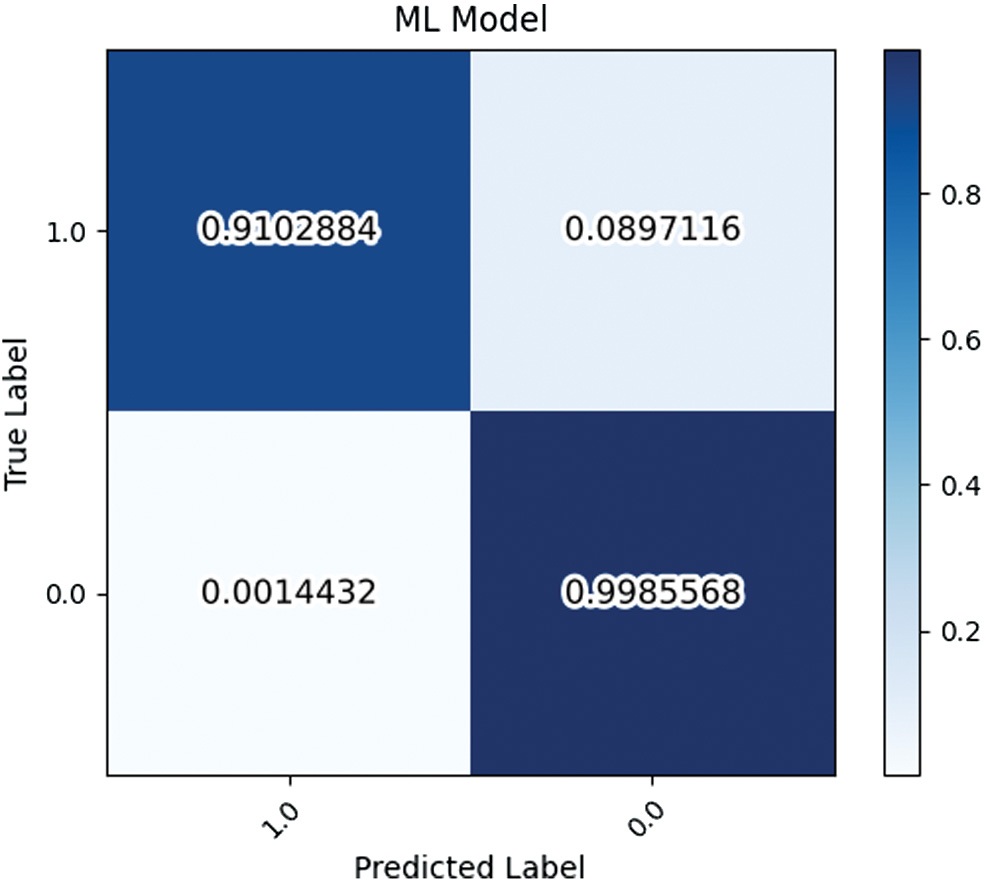Fig. 5. Confusion Matrix for ML model.
Fig. 6. Confusion Matrix for ASTRiDE.
Fig. 7. Confusion Matrix for Pyradon.
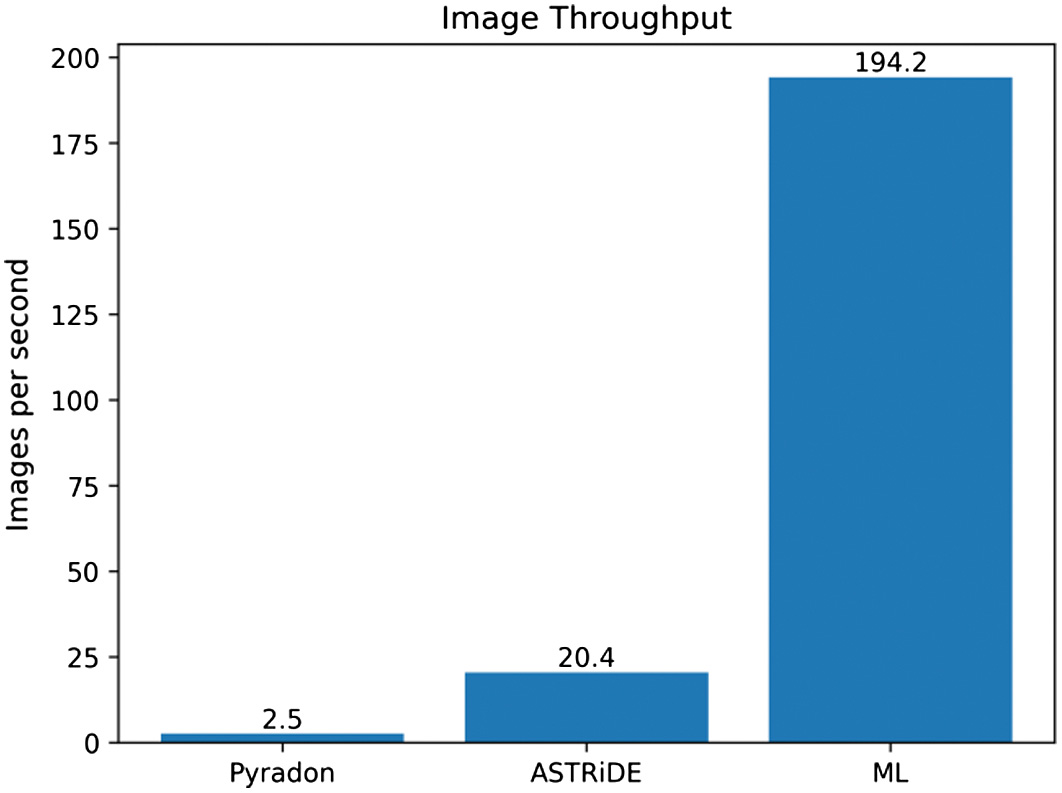
The number of samples (2000) was divided by the measured execution time for each method, yielding the average image processing throughput for each method as shown in Fig. 8. For consistency, all benchmarks were performed on the same system (see earlier).
V.DISCUSSION
For MAE, ASTRiDE and the ML model appear to have similar performance; however, Pyradon is significantly less accurate overall. When MSE is considered, ASTRiDE performs much worse relative to the ML model. This indicates a number of cases where ASTRiDE had significant error which MSE amplifies. Pyradon continues to perform the worst, being over two orders of magnitude worse than the ML model.
From the confusion matrices, it is apparent that ASTRiDE struggles with FN labels, with over 33% of true streak pixels marked as negative by it. By contrast, the ML model and Pyradon have very low rates of false-negative detections. Analyzing false positives, ASTRiDE performs the best, with only a 0.07% false-positive detection rate. By comparison, the ML model achieves a false-positive rate of 0.14% and Pyradon 1.9%. Figure 9 gives a visual representation of the example streaks from Fig. 10 color-coded to denote FN, FP, TN, and TP.
Fig. 9. Analysis of the pixel accuracy of each method tested. Black denotes TN, blue denotes TP, red denotes FP, and green denotes FN.
Fig. 10. Example detection masks for Pyradon, ASTRiDE, and our ML model compared to the ground truth and the raw image.
Examination of sample predictions from each method gives insight into certain behaviors that may be undesirable. A prototypical example can be seen in Fig. 10, where ASTRiDE tends to include nearby noise artifacts in the detection mask, needlessly masking out pixels that may otherwise contain good data. There is also evidence that ASTRiDE is unable to create a mask in certain situations. For example, as seen in Fig. 11, ASTRiDE will not generate a mask when a streak crosses the border of the image. This is because the boundary tracing algorithm is unable to complete a polygon when the edge of the object is not visible in the image. The result is a large error across all metrics for these instances.
Fig. 11. An image containing a satellite streak that partially intersects with the edge of the frame and the corresponding mask generated by ASTRiDE.
Pyradon also has issues with false positives which are easily visualized. Figure 10 shows Pyradon attempting to mask the same streak, but failing to correctly terminate at the ends of the streak.
In contrast, our ML model produces a uniform and well-formed mask of the same streak; however, it does so with some notable “aliasing” artifacts caused by the lower-resolution downscaled images that the model requires as an input.
Analysis of IoU for each method indicates the same performance rankings as previous metrics; however, ASTRiDE’s occasional failure to generate a mask becomes more apparent with its IoU score of 0.514 relative to Pyradon’s score of 0.431. These instances of 0 overlap significantly harm ASTRiDE’s score in this metric. Our ML model performs very well when measured by IoU, scoring 0.803, and indicating very strong overlap.
Analysis of the SOF for each method indicates how well each method avoids masking valid data, as seen in Table II. When measuring the SOFb which excludes stars covered by a streak, ASTRiDE performs the best at 1.07%, with our ML model close behind at 1.50%. Pyradon demonstrates a significant tendency to mask out valid pixels containing stars with an average SOFb of 7.17%.
When measuring SOFa which includes all stars in the frame, we gain the context of the total amount of valued data excluded by each method. The average SOFa from applying the ground truth mask to the image is 9.27% for our dataset. The ML model is close to this at 9.25%, the small reduction relative to the ground truth mask being indicative of a slightly undersized mask leaving exposed some intersected star pixels. Pyradon scores significantly worse at 12.98%. However, ASTRiDE has an average SOFa of 6.34%, below the value set by the ground truth. This is possible because of ASTRiDE’s tendency to omit generating a mask at all in some situations. The result of this, in combination with ASTRiDE’s low SOFa outside of pixels contained in streaks, is that ASTRiDE will not mask pixels containing both a streak and a star that otherwise should be masked, resulting in the anomalously low SOFa in this situation.
When comparing the execution speed of each method, our ML model is significantly faster than either of the traditional methods, being capable of processing nearly 10× as many images as ASTRiDE in the same amount of time. This could be useful in situations where large amounts of data need to be processed quickly in near real time, such as astronomical surveys.
VI.CONCLUSION
In this paper, we have developed and evaluated an ML approach for detecting and masking satellite streaks in astronomical data. The traditional methods ASTRiDE and Pyradon had problematic results with high levels of false negatives and false positives, respectively, while our method outperformed these traditional methods on the whole. We also have applied a novel metric, SOF, for the evaluation of masking methods’ tendency to mask valid data. Under SOF, our model also demonstrated a significantly lower tendency to erroneously mask out valid star data than Pyradon and a tendency comparable to ASTRiDE. This demonstrates our model’s capability to retain important valid data while masking invalid streak data.
Simultaneously, our method required significantly less computing resources and was able to execute significantly faster than either of the traditional methods tested. Therefore, our novel ML model outperforms comparable traditional methods at this task, achieving a very low false-negative rate while maintaining an acceptably small number of false positives and retaining valuable data. At the same time, it provides these benefits on consumer-grade hardware.
In the future, we plan to evaluate the performance of other variants of U-Net as well as competing architectures. We could also investigate a hybrid system that utilizes aspects of both an ML model as well as some traditional detection techniques in order to achieve improved performance. Finally, we could explore the implementation of a ML model to remove noise and other distracting features from data in order to enhance the performance of traditional masking methods such as Pyradon and ASTRiDE.