JAIT

I.INTRODUCTION

Exoskeletal devices are widely used for rehabilitation of patients with disorders of the musculoskeletal system [1 –8]. The maximum effect is achieved when the patient and the exoskeleton form an integrated human-machine system (HMS), the effectiveness of which is determined by the degree of consistency (synchronicity) of the elements of this system, including the human and active exoskeleton [9 –12]. To meet this requirement, the system contains a human-machine interface (HMI), which is a technical means that provides interaction between the patient and the exoskeleton. This system, consisting of the patient, the exoskeleton, and HMI, was named bio-electromechanical system (BEMS).

The BEMS structure consists of an exoskeleton, a HMI, a patient, and a support surface.

At an early stage of rehabilitation, the patient occupies a passive position, and the movements of the lower limbs are performed using an exoskeleton along program-defined trajectories in accordance with the rehabilitation exercises performed, for example, the patient’s walking on a path.

At later stages, a combined mode of BEMS operation is possible, in which at certain times the patient takes an active position and the exoskeleton implements the movements set by the patient, and at another time, the operator switches to a passive mode, and the exoskeleton performs the movements set by the program.

Various control strategies are implemented in these modes [13 –15]. In the first case, we can talk about a tracking control system, and in the second one about a combination of tracking and copying control strategies. As the review of information sources shows, most scientific works consider walking on a fixed base [16 –18], which in most cases reflects the real conditions of the use of walking machines, but in the case of creating a rehabilitation complex, the task of studying walking on a movable base, synchronizing the movement of the walking device, and the moving surface is relevant [19,20].

The design of the exoskeleton considered in this work is equipped with special sensors system that allows assessing the interaction forces between the operator and the exoskeleton [19]. Also, an important feature of the work is the use of piecewise polynomial functions when specifying the exoskeleton foot movement trajectory.

The device studied in the article is intended for mechanotherapy for patients with lower extremities musculoskeletal system dysfunctions [6,17].

The main contributions of this paper are as follows:

−the mathematical models of BEMS executive units movement,
−the new trajectory planning method,
−algorithms of the system motion control that provides collaborative functioning of the human exoskeleton and the movable supporting surface,
−the numerical modeling results, proving the proposed methods applicability in the exoskeleton practical implementation.

II.MATHEMATICAL MODEL AND FORMULATION OF THE SIMULATION PROBLEM

The paper deals with the lower limbs’ exoskeleton during the walk implementation along the moving belt of a treadmill (Fig. 1). The upper part of the exoskeleton 1 is attached to a fixed base – the frame. The femoral links 2 (left leg) and 4 (right leg) by means of active joints that contain electric drives creating moments, that can have an assisting effect on the patient, are attached to the body. To control the relative position of the links, the active hinges are equipped with angle sensors and torque sensing systems. In a similar way, the femoral links are connected to the lower leg links 3 (left leg) and 5 (right leg).

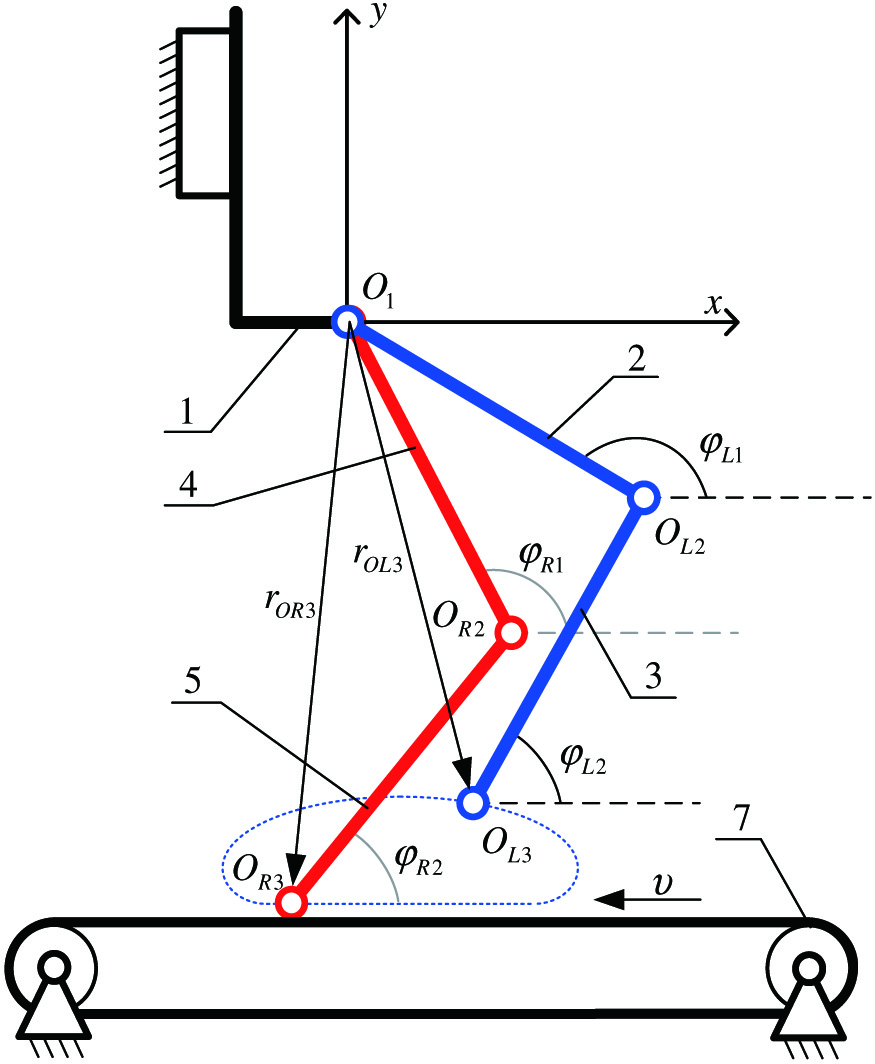FIGURE 1. Design diagram of the device in the process.

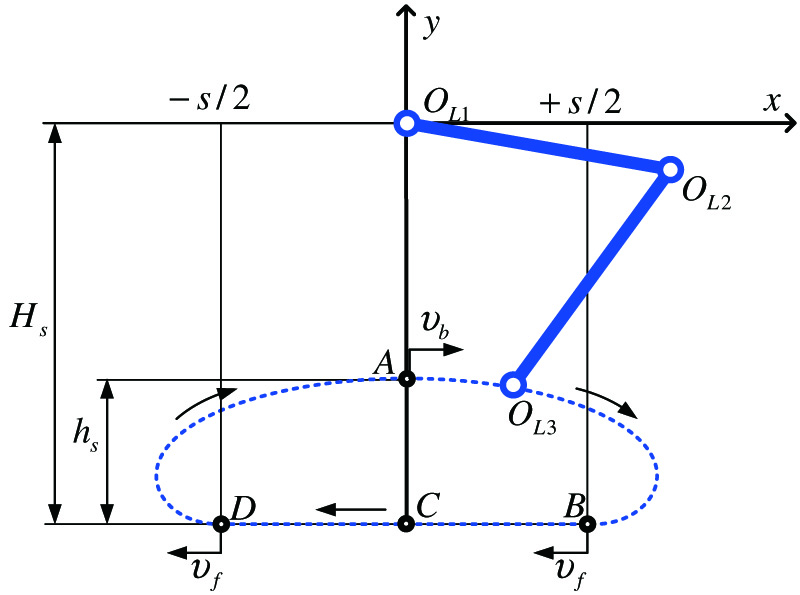FIGURE 2. Planning the trajectory of moving links of a walking machine.

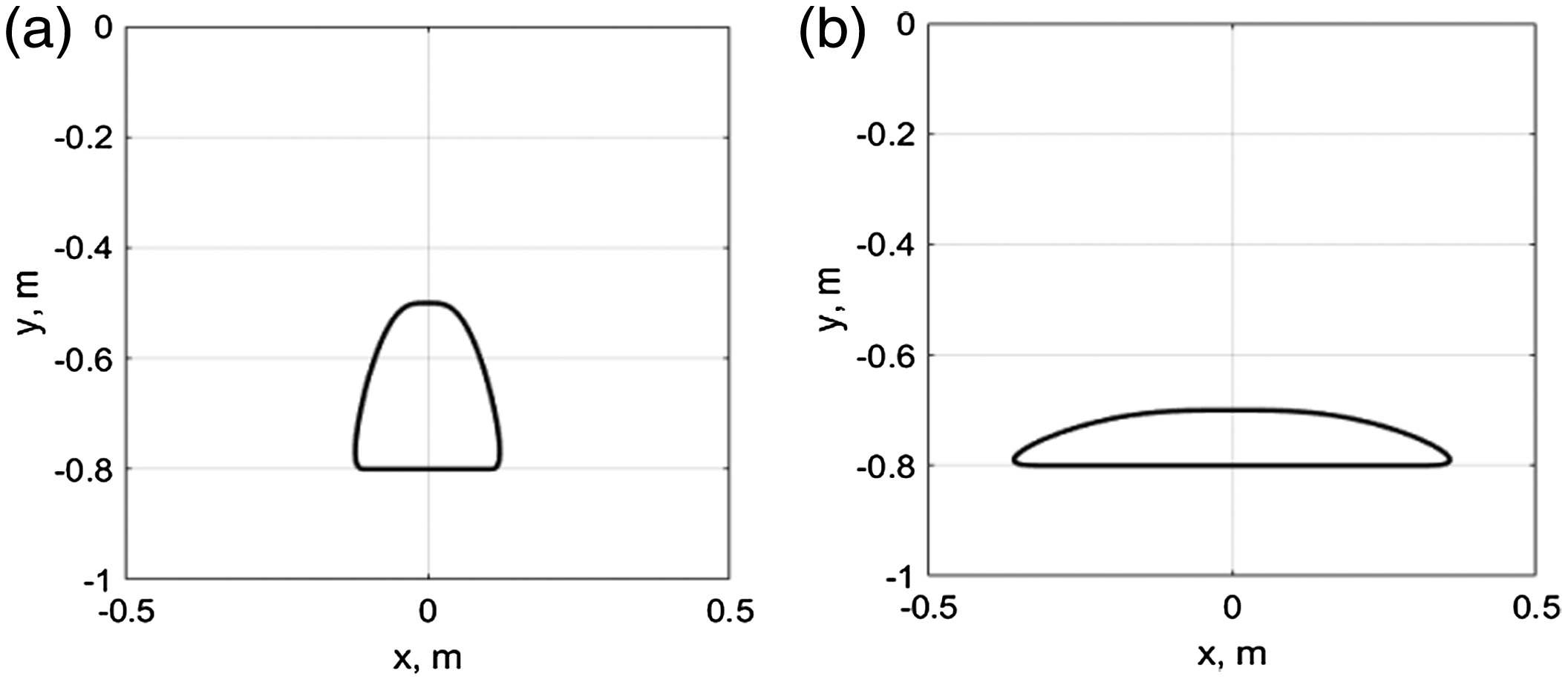FIGURE 3. Trajectories defined by equations (6)–(9) for the step parameters: (a) s¯=(0.2,0.3,0.7,0.5,4)T, (b) s¯=(0.6,0.1,0.8,0.25,4)T.

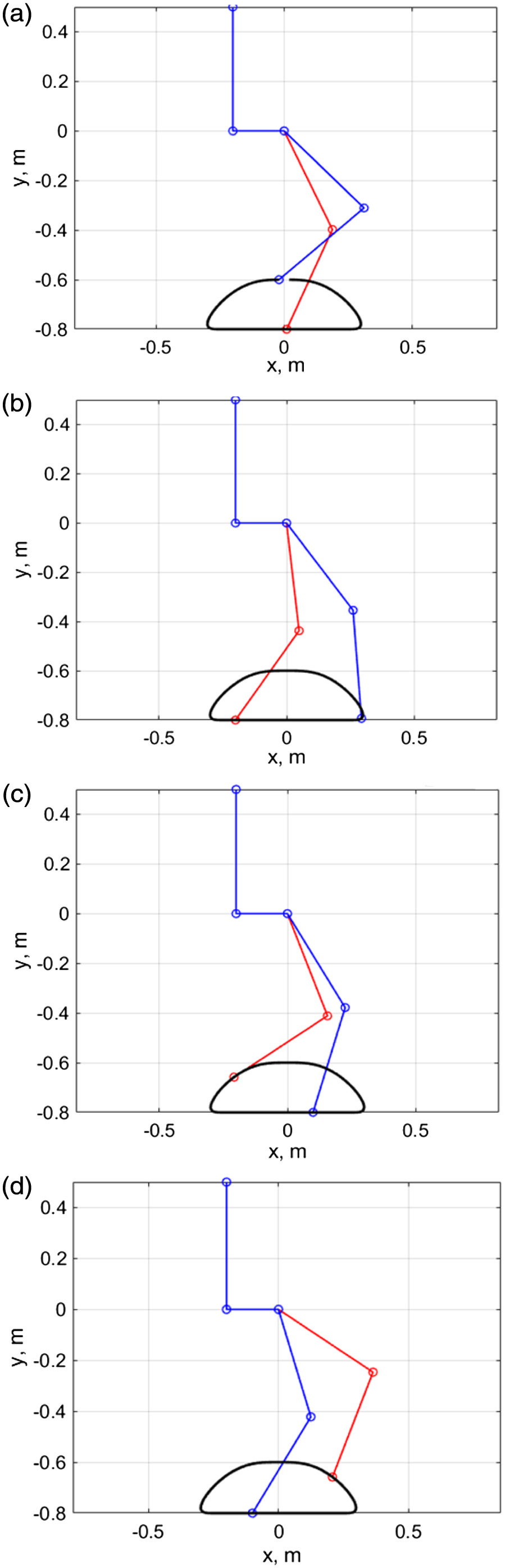FIGURE 4. Walking simulation results: a – at 0 s, b – at 0.2 s, c – at 0.4 s, d – at 0.6 s.

The task of the system that controls drives of the hip and knee joints of the device is to realize this relative motion of links, at which points $O_{L 3}$ and $O_{R 3}$ move along the desired trajectory, implementing a walking motion of the exoskeleton. An important feature of the desired trajectory is to ensure that there is no slippage or impact at the moment of contact with the surface, which is provided by the choice of appropriate boundary conditions. In this work, there are number of assumptions: The trajectory of the foot attachment point is symmetrical with respect to the vertical axis, the movable surface is parallel to the horizon, the size and shape of the feet are neglected, considering that the contact of the robot’s links with the surface occurs through the points $O_{L 3}$ and $O_{R 3}$ .

For mathematical description of the kinematics of motion, there is a system of equations:

\begin{matrix} x_{O L 2} = x_{O} + l_{1} \cos (ϕ_{L 1}) \\ y_{O L 2} = y_{O} + l_{1} \sin (ϕ_{L 1}) \\ x_{O R 2} = x_{O} + l_{1} \cos (ϕ_{R 1}) \\ y_{O R 2} = y_{O} + l_{1} \sin (ϕ_{R 1}) \end{matrix}; \begin{matrix} x_{O L 3} = x_{O} + l_{1} \cos (ϕ_{L 1}) + l_{2} \cos (ϕ_{L 2}) \\ y_{O L 3} = y_{O} + l_{1} \sin (ϕ_{L 1}) + l_{2} \sin (ϕ_{L 2}) \\ x_{O R 3} = x_{O} + l_{1} \cos (ϕ_{R 1}) + l_{2} \cos (ϕ_{R 2}) \\ y_{O R 3} = y_{O} + l_{1} \sin (ϕ_{R 1}) + l_{2} \sin (ϕ_{R 2}) \end{matrix}

where

l_{1}

and

l_{2}

are long links, respectively: thighs and shins,

x_{O}

y_{O}

– are coordinates of the femoral joint in the inertial reference system,

ϕ_{L i}

ϕ_{R i}

are absolute rotation angles of the left and right leg links.

The links’ rotation angles can be determined in various ways, in the framework of this work, they are defined as follows:

ϕ_{L 1} = {\begin{cases} a r c t n g (\frac{y_{O L 3}}{x_{O L 3}}) + \arccos (\frac{l_{1}^{2} - l_{2}^{2} + (x_{O L 3}^{2} + y_{O L 3}^{2})}{2 l_{1} \sqrt{x_{O L 3}^{2} + y_{O L 3}^{2}}}) & if (x_{O L 3} > 0) \\ a r c t n g (\frac{y_{O L 3}}{x_{O L 3}}) + \arccos (\frac{l_{1}^{2} - l_{2}^{2} + (x_{O L 3}^{2} + y_{O L 3}^{2})}{2 l_{1} \sqrt{x_{O L 3}^{2} + y_{O L 3}^{2}}}) - π & if (x_{O L 3} \leq 0) \end{cases} ϕ_{L 2} = ϕ_{L 1} + (π + \arccos (\frac{l_{1}^{2} + l_{2}^{2} - (x_{O L 3}^{2} + y_{O L 3}^{2})}{2 l_{1} l_{2}}))

Using these equations, it is possible to determine the absolute rotation angles of links when a point $O_{L 3}$ moves in the lower quadrants of the coordinate plane $(y_{O R 3} < 0)$ . The angles $ϕ_{R 1}$ , $ϕ_{R 2}$ for the second leg of a walking machine can be obtained in a similar way.

III.TRAJECTORY PLANNING

The trajectories of the points $O_{L 3}$ and $O_{R 3}$ are determined by the mechanism parameters, type of gait, and step parameters. Let us introduce a coefficient that determines the shape of the trajectory of the points $k_{υ} = υ_{f} / υ_{b}$ , where $υ_{f}$ is the speed along the linear part of the trajectory (movement together with the support), $υ_{b}$ is the maximum foot speed; for the symmetrical walking, it is the upper intersection point of the trajectory with the ordinate axis.

Using the coefficient, we can obtain a vector of gait parameters, $\bar{s} = {(s, h_{s}, H_{s}, k_{υ}, T_{s})}^{T}$ in which $s$ is the step length, $h_{s}$ is the height of the leg when walking, $H_{s}$ is the distance from the hip joint to the treadmill running, $T_{s}$ is the duration of one step. Note that the parameters $s$ and $T_{s}$ determine the walking speed and can be calculated based on the speed of the moving base.

Since the trajectory is symmetrical, it is convenient to use a piecewise polynomial function, splitting it into 3 fragments: $A B$ , $B D$ , $D A$ .

In order to provide the continuity of the trajectory setting functions, as well as the lack of collision of the links on the surface, the conditions must be met at each point. Next, an example related to the function for left leg is presented and performed (for the right, leg the function is going to be similar):

At point A : {\begin{cases} x_{O L 3} = 0; \\ y_{O L 3} = - (H_{s} - h_{s}); \\ {\dot{x}}_{O L 3} = υ_{b}; \\ {\dot{y}}_{O L 3} = 0. \end{cases}

At point B : {\begin{cases} x_{O L 3} = s / 2; \\ y_{O L 3} = - H_{s}; \\ {\dot{x}}_{O L 3} = - υ_{f}; \\ {\dot{y}}_{O L 3} = 0. \end{cases}

At point D : {\begin{cases} x_{O L 3} = - s / 2; \\ y_{O L 3} = - H_{s}; \\ {\dot{x}}_{O L 3} = - υ_{f}; \\ {\dot{y}}_{O L 3} = 0. \end{cases}

Polynomial functions for changing coordinates can be represented as follows:

\bar{q} (t_{0}, t_{l a s t}, q_{0}, q_{l a s t}, {\dot{q}}_{0}, {\dot{q}}_{l a s t}, t) = (\sum_{i = 0}^{3} k_{i} t^{i})^{T}

where coefficients

k_{i}

are determined by:

[\begin{matrix} k_{0} \\ k_{1} \\ k_{2} \\ k_{3} \end{matrix}] = [\begin{matrix} 1 & t_{0} & t_{0}^{2} & t_{0}^{3} \\ 1 & t_{l a s t} & t_{l a s t}^{2} & t_{l a s t}^{3} \\ 0 & 1 & 2 t_{0} & 3 t_{0}^{2} \\ 0 & 1 & 2 t_{l a s t}^{} & 3 t_{l a s t}^{2} \end{matrix}] \cdot [\begin{matrix} q_{0} \\ q_{l a s t} \\ {\dot{q}}_{0} \\ {\dot{q}}_{l a s t} \end{matrix}]

where

t_{0}

is initial time of the trajectory fragment,

t_{l a s t}

is final time,

q_{0}, {\dot{q}}_{0}

is initial value of the coordinate and its derivative,

q_{l a s t}, {\dot{q}}_{l a s t}

is final value of the coordinate and its derivative corresponding to the trajectory fragment.

In order to record the simultaneous trajectories of the both legs of the device, an additional point has been introduced into the trajectory. This point corresponds to the A point in the trajectory for the other leg. Trajectory recalculating in a loop can be implemented as a function mod (a, b). This function returns the remainder of dividing a by b. Thus, the use of the equations for coordinates $O_{L 3}$ and $O_{R 3}$ becomes possible by setting the length of the step $T_{s}$ and dividing it by 8 equal intervals $[t_{A}, t_{B}),$ $[t_{B}, t_{C}),$ $[t_{C}, t_{D}),$ $[t_{D}, t_{A}) \in t$ , where $t = \mod (T i m e, T_{s})$ , Time is current time value.

{\begin{cases} x_{O L 3} = q (t_{A}, t_{B}, 0, (s / 2), υ_{b}, - υ_{f}, t); \\ y_{O L 3} = q (t_{A}, t_{B}, - (H_{s} - h_{s}), - H_{s}, 0, 0, t); \\ x_{O R 3} = - t υ; \\ y_{O R 3} = - H_{s}; \end{cases} if (t_{A} \leq t < t_{B})

{\begin{cases} x_{O L 3} = - t υ_{f} + s; \\ y_{O L 3} = - H_{s}; \\ x_{O R 3} = q (t_{B}, t_{C}, (- s / 2), 0, - υ_{f}, υ_{b}, t); \\ y_{O R 3} = q (t_{B}, t_{C}, - H_{s}, - (H_{s} - h_{s}), 0, 0, t); \end{cases} if (t_{B} \leq t < t_{C})

{\begin{cases} x_{O L 3} = - t \cdot υ + s; \\ y_{O L 3} = - H_{s}; \\ x_{O R 3} = q (t_{C}, t_{D}, 0, (s / 2), υ_{b}, - υ_{f}, t); \\ y_{O R 3} = q (t_{C}, t_{D}, - (H_{s} - h_{s}), - H_{s}, 0, 0, t); \end{cases} if (t_{C} \leq t < t_{D})

{\begin{cases} x_{O L 3} = q (t_{A}, t_{D}, (- s / 2), 0, - υ_{f}, υ_{b}, t); \\ y_{O L 3} = q (t_{A}, t_{D}, - H_{s}, - (H_{s} - h_{s}), 0, 0, t); \\ x_{O R 3} = - t υ_{f} + 2 s; \\ y_{O R 3} = - H_{s}; \end{cases} if (t_{D} \leq t < t_{A})

By setting the step parameter values, it becomes possible to obtain different trajectories of the $O_{L 3}$ point movement.

As shown in the graphics, the developed trajectory planning algorithm allows obtaining a continuous trajectory for multiple step parameters. When the coefficient $k_{υ}$ decreases, the trajectory becomes elongated, due to the synchronization requirements imposed to the links movement, which are composed of a movable base (collision is not stipulated).

Using the trajectory shape coefficient $k_{υ}$ results possible to obtain the required law of movement of links. This law is necessary to establish the parameters of the mechanotherapy of a specific patient, which simplifies the configuration and preparation of equipment.

IV.NUMERICAL SIMULATION OF THE MOVEMENT KINEMATIC OF THE ACTING LINKS OF A TWO-LEGGED WALKING MACHINE-EXOSKELETON ON A MOVABLE BASE

Mathematical modeling of the device movement at walking on a movable base stage has been performed. The length of the links of the device (0.5 m), as well as the step parameters $\bar{s} = {(0.5, 0.2, 0.8, 0.5, 1)}^{T}$ , has been specified.

In Fig. 5, a space-time diagram for the coordinates $O_{L 3}$ and $O_{R 3}$ is presented.

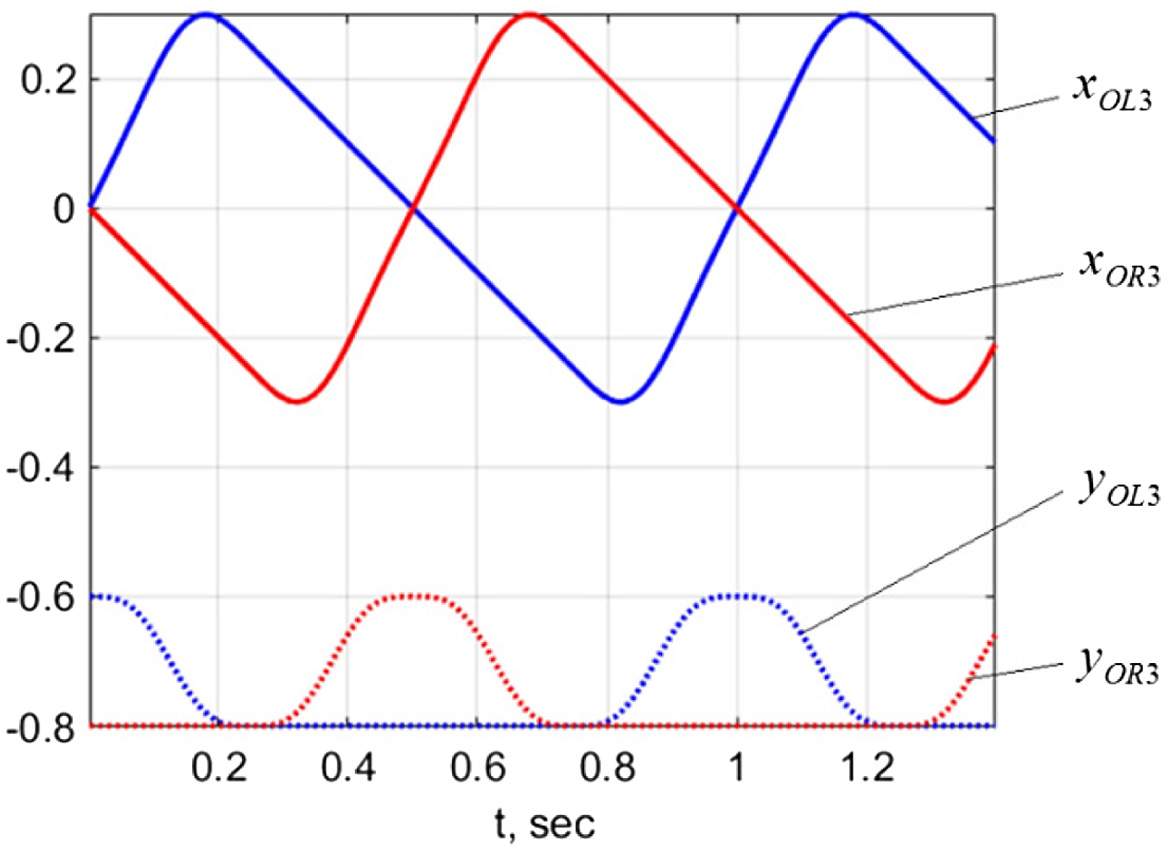FIGURE 5. Law of change of the coordinates OL3 и OR3 at trajectory performing.

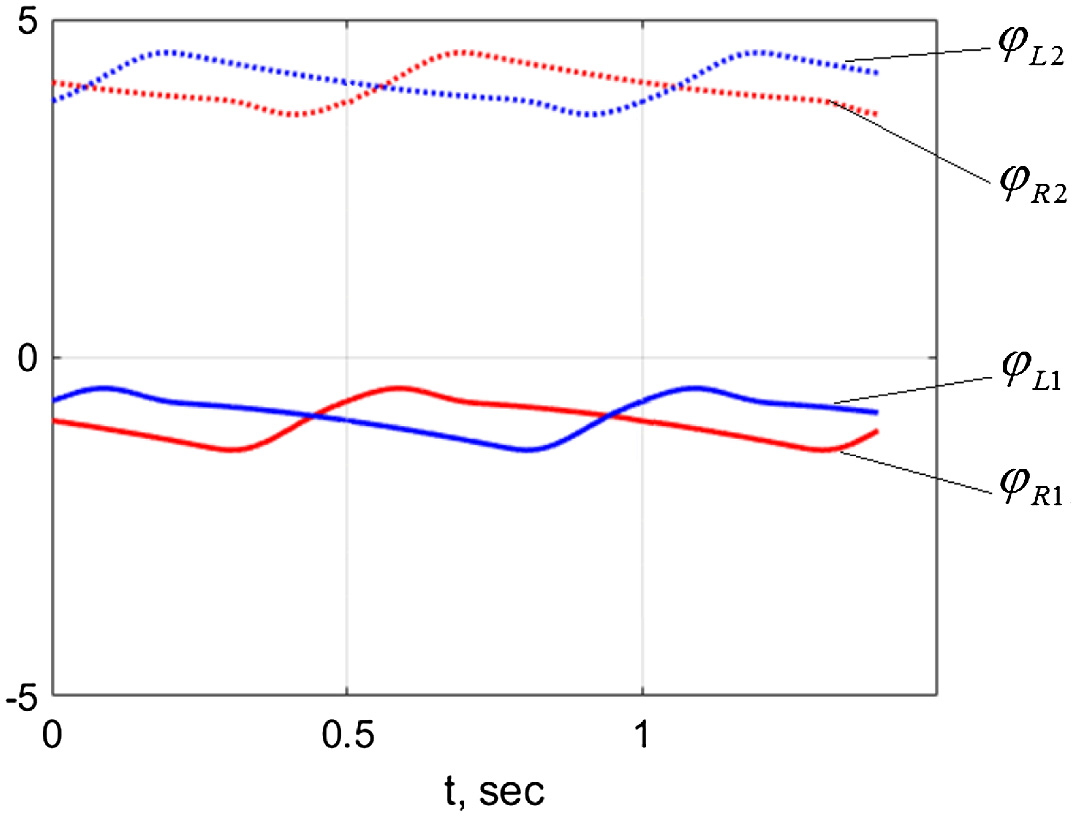FIGURE 6. Laws of change of the absolute angles of rotation of the device links at trajectory performing.

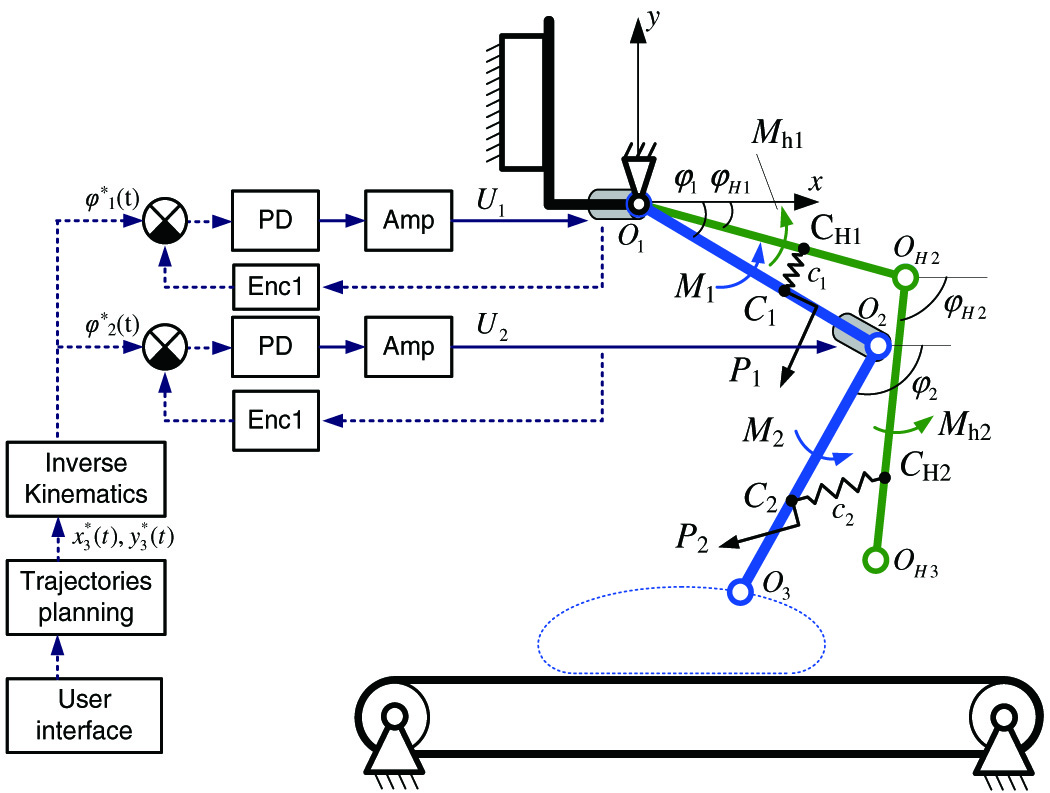FIGURE 7. Design diagram of the device and control system structure.

During the modeling process, absolute and relative angles related to the movement of the links were also obtained when the symmetrical trajectory of movement of the links of the acting mechanism of the two-legged walking machine on a horizontal movable base is performed.

V.CONTROL SYSTEM AND HUMAN-MACHINE SYSTEM DESIGN

In order to setup the coefficients of the regulators, adjust the HMS and other system parameters, it is necessary to perform a mathematical modeling of the control system of the links of the exoskeletal system.

Since the control loops for the left and right legs are the same and differ only in the phases of the trajectories, we will describe one leg in the simulation process. Also, we will not consider the interaction of the patient’s foot and the corresponding nodes of the exoskeletal system. In many rehabilitation devices designed to simulate walking and rehabilitation of the hip and knee joints, the ankle joint does not contain actuators, in these cases, the foot is simply fixed on elastic elements that provide comfort to the patient [12,20].

The control task is reduced to working out the required trajectory of movement. The principle of operation of the HMS is as follows. The patient or the exoskeleton operator selects the necessary mode and the parameters of the exercise and starts its execution. Next, the trajectory construction unit synthesizes the laws of changing the coordinates of the foot joint $x_{3}^{*} (t), y_{3}^{*} (t)$ . Then, the values of the required coordinates $x_{3}^{*} (t), y_{3}^{*} (t)$ are transmitted to the unit for determining the setting angles for the drive control system $φ_{1}^{*} (t), φ_{2}^{*} (t)$ . The required rotation angles are fed to the input of the PD controller, where the control voltages for the electric motors of the exoskeleton are generated:

U_{i}^{} = k_{p} (ϕ_{i}^{*} - ϕ_{i}) + k_{d} ({\dot{ϕ}}_{i}^{*} - {\dot{ϕ}}_{i})

where,

k_{p}, k_{d}

are coefficients of the PD controller. The coefficients of the regulator were selected as result of computational experiments.

Thus, the legs of the exoskeleton and patient can be represented by two-coordinate pendulums with a common base and connected each other by elastic elements that simulate the operation of the cuffs, whereas the links of the exoskeleton will be driven by the moments of electric drives equipped with a position control system.

In this case, the system of differential equations describing the leg of the exoskeleton will take the form:

{\ddot{ϕ}}_{1} l_{1}^{2} (m_{1} + m_{2}) + {\ddot{ϕ}}_{2} m_{2} l_{1} l_{2} \cos (ϕ_{1} - ϕ_{2}) + {\dot{ϕ}}_{2}^{2} m_{2} l_{1} l_{2} \sin (ϕ_{1} - ϕ_{2}) = = M_{1} - P_{1} l_{P 1} \sin (γ_{1} - ϕ_{1}) - P_{2} l_{P 1} \sin (γ_{2} - ϕ_{1}) - (m_{1} + m_{2}) g l_{1} \sin ϕ_{1}, {\ddot{ϕ}}_{2} l_{2}^{2} m_{2} + {\ddot{ϕ}}_{1} m_{2} l_{1} l_{2} \cos (ϕ_{1} - ϕ_{2}) - {\dot{ϕ}}_{1}^{2} m_{2} l_{1} l_{2} \sin (ϕ_{1} - ϕ_{2}) = = M_{2} - P_{2} l_{P 2} \sin (γ_{2} - ϕ_{2}) - m_{2} g l_{2} \sin ϕ_{2}, L \frac{d I_{1}}{d t} + R I_{1} + k_{Å} ϕ_{1} i_{G} = U_{1}, Ì_{1} = k_{m} I_{1}, L \frac{d I_{2}}{d t} + R I_{2} + k_{Å} ϕ_{2} i_{G} = U_{2}, Ì_{2} = k_{m} I_{2},

where,

m_{1}, m_{2}

are mass of the links of the exoskeleton,

l_{P 1}

l_{P 2}

γ_{1}

and

γ_{2}

are distance from the hinge to the point of application and the absolute angles of effort generated by the patient

P_{1}, P_{2}

, defined by the difference in the coordinates of the points

C_{1}, C_{H 1}

C_{2}, C_{H 2}

and also defined by the suspension stiffness

c_{1}, c_{2}

Ì_{1}

Ì_{2}

are torques generated by the drive,

k_{Å}

is the speed coefficient of the motor,

L

and

R

are inductance and active resistance of the motor armature winding,

i_{G}

is total gear ratio of the drive gearbox.

For the patient’s leg, described as a two-link mechanism, we can write similar equations:

{\ddot{ϕ}}_{h 1} l_{h 1}^{2} (m_{h 1} + m_{h 2}) + {\ddot{ϕ}}_{h 2} m_{h 2} l_{h 1} l_{h 2} \cos (ϕ_{h 1} - ϕ_{h 2}) + + {\dot{ϕ}}_{h 2}^{2} m_{h 2} l_{h 1} l_{h 2} \sin (ϕ_{h 1} - ϕ_{h 2}) = M_{h 1} + P_{1} l_{P 1 H} \sin (γ_{1 H} - ϕ_{h 1}) + + P_{2} l_{P 2 H} \sin (γ_{2 H} - ϕ_{h 1}) - (m_{h 1} + m_{h 2}) g l_{h 1} \sin ϕ_{h 1}, {\ddot{ϕ}}_{h 2} l_{h 2}^{2} m_{h 2} + {\ddot{ϕ}}_{h 1} m_{h 2} l_{h 1} l_{h 2} \cos (ϕ_{h 1} - ϕ_{h 2}) - - {\dot{ϕ}}_{h 1}^{2} m_{h 2} l_{h 1} l_{h 2} \sin (ϕ_{h 1} - ϕ_{h 2}) = M_{h 2} + + P_{2} l_{P 2 H} \sin (γ_{2 H} - ϕ_{h 2}) - m_{h 2} g l_{h 2} \sin ϕ_{h 2},

where

m_{h 1}, m_{h 2}

are mass of the hip and lower leg of the patient,

l_{P 1 H}

l_{P 2 H}

γ_{1 H}

, and

γ_{2 H}

distance from the hinge to the point of application and the absolute angles of effort generated by the exoskeleton.

Ì_{h 1}

Ì_{h 2}

are torques generated by the patient.

In this case, by setting the values of the torques, we can model the torques of resistance in the patient’s joints, including the phenomenon of spasticity, characterized by the appearance of uncontrolled muscle contractions, paralysis, and hypertonicity of the muscles.

VI.NUMERICAL SIMULATION OF THE MOVEMENT DYNAMICS OF THE ACTING LINKS OF A TWO-LEGGED WALKING MACHINE-EXOSKELETON ON A MOVABLE BASE

In this part of the work, we will perform a numerical simulation of the system by ignoring the torques in the patient’s joints $(M_{h s i} = 0)$ . The system parameters threshold ranges and the mathematical model used parameters are presented in Table 1.

Table I. Parameters of the mathematical model

Parameter description	Symbol	Used in the model value	Range of values
Mass of the femoral link of the exoskeleton	m₁	3.5 kg	–
Mass of the lower leg link of the exoskeleton	m₂	4.5 kg	–
Mass of the hip of the patient	m_h1	11.3 kg	7, 9.14, 7 kg
Mass of the lower leg, including the foot	m_h2	4.65 kg	3, 3.6, 0 kg
Length of the femoral link of the exoskeleton	l₁	0.52 m	0, 39.0, 65m
Length of the lower leg link of the exoskeleton	l₂	0.52 m	0, 39.0, 65m
Length of the hip of the patient	l_h1	0.52 m	0, 39.0, 65 m
Length of the lower leg of the patient	l_h2	0.52 m	0, 39.0, 65m
Distance from the hip to the hip cuff	l_hH	0.39 m	–
Distance from the knee to the cuff on the lower leg	l_hS	0.45 m	–
Cuff suspension stiffness coefficient	c_H,c_S	8 N/mm	6, 4.9, 6 N/mm
Armature winding inductance	L	0.072 mH	–
Armature winding resistance	R	0.103 Ω	–
Torque coefficient	k_m	0.35 Nm/A	–
Speed coefficient	k_E	25.9 rad/Vs	–

The parameters patient’s limbs lengths and masses are determined by the human physiological parameters. The values used for modeling correspond to the patient having a height of 175 sm and weight 80 kg.

In Fig. 8, the angular movements of the exoskeleton links and the operator’s limb during a single step are shown, as well as the torques on the electric drives and the projection of forces between the exoskeleton and the patient due to inertia and mass.

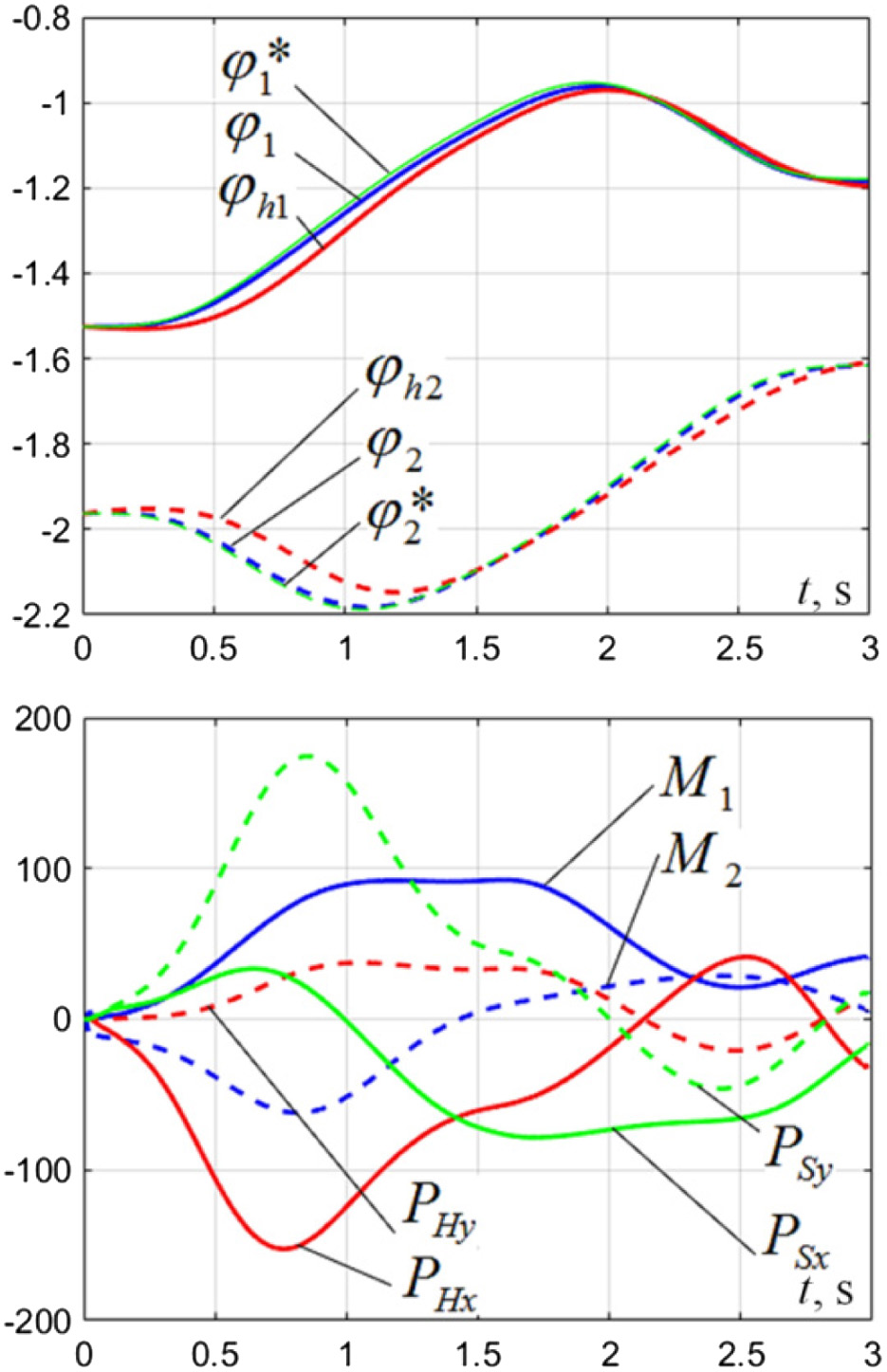FIGURE 8. The results of modeling the movement of the HMS at Mh1=Mh2=0.

In this case, as a trajectory, we take the characteristic movement of walking with the following parameters: The step width is 0.35 m, and the height of the leg lift is 0.1 m.

From the simulation results, we can observe that the actuators reach forces up to 100 Nm, with a maximum force of 200 N fixed in the ankle cuff, when performing a step.

The selection of movement parameters and suspension parameters allows reducing the effort and moments, which can be useful when setting up a rehabilitation unit.

VII.CONCLUSION

A mathematical model of the movement of a two-legged walking mechanism on a movable base of a treadmill has been carried out. A method for studying this mechanism has been proposed. Also, trajectory planning algorithms have been developed, and the equations for solving the inverse kinematics problem for the mechanism links have been written. In order to set the shape of the trajectory, a coefficient $k_{υ}$ is proposed. This coefficient represents the relationship between the speed values of movement of the legs on the surface and above the surface. Also, this coefficient in conjunction with other step parameters, such as length, height, and duration, allows getting the required movement of the links of the walking mechanism, which are necessary for conducting a mechanotherapy treatment. The presented method is approved by mathematical modeling, which demonstrates the applicability and appropriate operation of the developed algorithms for trajectory planning for robot-exoskeleton devices.

In this paper, a block diagram of the control system is proposed. This control system diagram describes the strategy of generating the required supply voltages for the drives of the exoskeleton when working out the trajectory. The presented mathematical model allows taking into account the dynamics of the HMS as well as to obtain the load diagrams for the drives of the device in walking mode and estimate the value of the forces arising between the exoskeleton and the patient due to the existence of inertia and gravity.

In the future researches, it is planned to develop a prototype of a rehabilitation complex for practical investigation of the proposed models and algorithms, as well as their modernization to meet the requirements of rehabilitation doctors.

Simulation of a Walking Robot-Exoskeleton Movement on a Movable Base

I.INTRODUCTION

II.MATHEMATICAL MODEL AND FORMULATION OF THE SIMULATION PROBLEM

III.TRAJECTORY PLANNING

IV.NUMERICAL SIMULATION OF THE MOVEMENT KINEMATIC OF THE ACTING LINKS OF A TWO-LEGGED WALKING MACHINE-EXOSKELETON ON A MOVABLE BASE

V.CONTROL SYSTEM AND HUMAN-MACHINE SYSTEM DESIGN

VI.NUMERICAL SIMULATION OF THE MOVEMENT DYNAMICS OF THE ACTING LINKS OF A TWO-LEGGED WALKING MACHINE-EXOSKELETON ON A MOVABLE BASE

VII.CONCLUSION

ACKNOWLEDGMENTS

REFERENCES