I.INTRODUCTION

The rapid development of artificial intelligence technology has placed various industries in a new era of high digitization and rapid intelligence. The application of artificial intelligence in social life has brought unprecedented convenience and opportunities to people. At the same time, people have also conducted research on deeper and more extensive applications in the field of artificial intelligence [1]. Among them, the research and simulation of intelligent robots based on reinforcement learning has become a highly concerned field. Traditional handmade seal carving has a long history and profound cultural heritage. However, there are many limitations and defects in the process of manual seal cutting, such as long production cycles, high requirements for human skills, and difficulty in ensuring engraving accuracy [2]. With the continuous development of artificial intelligence technology, its application in the cultural field is becoming increasingly widespread. Using artificial intelligence to inject new vitality into traditional culture has become an important means of cultural inheritance. With the rapid development of artificial intelligence and robotics technology, seal engraving robots have become a research hotspot. The existing methods mainly include traditional image processing techniques, template matching techniques, and machine learning methods. However, the accuracy and robustness of these methods still need to be improved when dealing with complex seal patterns and multilingual seals [3]. Reinforcement learning can enable robots to make intelligent decisions in seal making, adapting to the needs of seal making with different shapes and complexities. However, existing reinforcement learning methods often overlook the flexibility requirements of robots when executing actions, resulting in robots being unable to flexibly cope with various situations in actual operations. The point cloud model (PCM) can effectively handle complex geometric shapes and topological relationships, providing a solid data foundation for subsequent reinforcement learning algorithms. Using PCMs to analyze the characteristics of seals, combined with flexible action evaluation algorithms, enables robots to achieve more precise and flexible seal cutting actions. In this context, research attempts to innovatively combine deep reinforcement learning convolutional neural networks (CNNs) and PCMs to recognize seal information based on object detection and improve recognition accuracy by improving the algorithm steps and structure. Innovatively combining deep strategy gradient algorithm with reinforcement learning technology is to reconstruct the objective function and achieve research and simulation of seal engraving robots. It is urgent to provide feasible technical references for the seal engraving industry.

This study conducts technical exploration and analysis from four aspects. The rest of the paper is structured as follows. Section II discusses and summarizes the current research on robot intelligence technology. Section III mainly calculates and analyzes the comprehensive utilization of deep reinforcement learning and seal cutting optimization algorithms and also includes the design and construction of seal cutting robots. Section IV focuses on mainly conducted experimental verification and data analysis comparison on the text recognition algorithm model. Section V provides a comprehensive overview of the entire article, reflecting on and summarizing the shortcomings.

II.RELATED WORK

The rapid development of robots and artificial intelligence technology have made robot intelligence in social life and become a key research field for both academia and industries [4,5]. Yin F et al. focused on the control problem of the robotic arm during the carving process of stone carving robots, using deep reinforcement learning basis function neural networks. It combines the Lagrange method to propose an adaptive terminal sliding mode control strategy for the robotic arm, thereby improving the response speed and high-precision control of the robotic arm during the carving process of the stone carving robot [6]. Hashan A M et al. proposed a computer numerical controlled two-dimensional drawing robot based on computer-aided design of CNC machine tools to address the application of robots in drawing. This method increases the possibility of robots being applied in the field of art [7]. Yin F et al. also proposed a robotic arm control system based on inverse linear-quadratic theory for the control optimization problem of stone carving robots. This system improves the optimal control performance of the robotic arm [8]. Biglari H et al. focused on the control problem of flexible engraving robot arms based on internal friction dampers. They combined particle swarm optimization algorithm, empire competition algorithm, non-dominated sorting genetic algorithm, and gray wolf optimization algorithm to propose a flexible carving robot control algorithm. The proposed algorithm improves the arm control accuracy of flexible robots [9]. Bollars P et al. proposed an imageless robotic surgery system based on bone mapping, digital gaps, and alignment data to address the issue of carving alignment in total knee replacement surgery. It improved the efficiency of full knee joint carving alignment [10]. Wang et al. proposed a design method for stone carving robots based on 3D design software to address the design issues of stone carving robots. This method shortens the design time of stone carving robots [11]. Regarding the problem of automated robot processing for irregular stone carvings, Xing et al. study is based on the time planning spatial hybrid parallel manipulator structure. They combined kinematic models and Jacobian matrices to propose a sculpting model for a special-shaped stone carving robot. This model improved the automation efficiency of irregular stone carving [12]. Yin et al. focused on the optimization problem of stone carving robots using particle swarm optimization algorithm based on reinforcement learning. Combining support vector machines, a milling force control and optimization method for engraving robots has been proposed, thereby improving the overall engraving processing quality [13]. Ji et al. focused on the intelligent manufacturing problem of robots, based on the automatic programming environment under reinforcement learning algorithms. It combines power circuit breakers and electronic set-top boxes to propose an automated robot assembly system, improving the efficiency of robot intelligent manufacturing [14]. Ercan Jenny et al. focused on the automation of gypsum processing in buildings, based on gypsum technology and construction methods. It combines automated robot technology to construct a robot gypsum treatment system, thereby improving the intelligent efficiency of building gypsum treatment [15]. Capunaman et al. focused on the recognition of carved surfaces by robots during the carving process, based on deep reinforcement learning CNNs. A sensor framework based on visual technology has been designed to enhance the robot’s adaptability to uncertain surfaces [16]. Fang et al. focused on the trajectory planning and control problem of intelligent agents, based on scene perception and trajectory prediction. They proposed an aggregated autonomous driving framework, which enhances the safety of intelligent delivery for autonomous guided vehicles [17]. Li et al. focused on the intelligence of traditional carving equipment and based it on machine vision using deep reinforcement learning CNNs. The establishment of an intelligent comprehensive control system for pattern carving has improved the intelligence and informatization of carving equipment [18].

From the research of scholars from various countries, most research on robot intelligence mainly focuses on optimizing a single link, neglecting the overall system interaction between intelligent robots and the environment. Therefore, this study is based on deep reinforcement learning CNNs, combined with PCMs, proximal strategy optimization algorithms, and flexible action evaluation algorithms. The proposed seal cutting robot based on deep reinforcement learning has certain innovation.

III.SEAL RECOGNITION AND CUTTING ROBOT BASED ON REINFORCEMENT LEARNING

Unlike traditional robot models, the seal cutting robot that integrates PCMs, proximal strategy optimization algorithms, and flexible action evaluation algorithms has a certain degree of innovation. In order to continuously optimize the algorithm model, its design and implementation are particularly important. Therefore, this section mainly analyzes the basic principles of the model and the construction of the system.

A.REINFORCEMENT LEARNING TECHNOLOGY FOR SEAL RECOGNITION

The traditional handmade seal cutting text presents different rhythmic and natural curves based on the differences of craftsmen. Although the text carved by robots is precise, it is relatively rigid and uniform, and it is a copy of the font text without any artistic value. Therefore, research first requires high-precision automatic image recognition and analysis of physical seals carved in various artworks, laying the foundation for humanoid seal carving. The task of target detection (TD) is to detect and recognize the required objects in the image through information such as target type features and spatial position features [19]. In the research of seal cutting robots, reinforcement learning can help robots learn how to select the best seal cutting tools and forces based on the input seal cutting patterns and requirements in order to achieve the expected results [20]. By using object detection algorithms, robots can monitor the position and shape of seals in real time and make adjustments and corrections as needed to ensure the accuracy and consistency of seal engraving [21]. The feature fusion classification network also plays an important role in the research of seal engraving robots. This network can fuse information with different features to improve the recognition and classification capabilities of seal cutting robots [22,23]. Figure 1 shows the TD technology roadmap based on deep reinforcement learning.

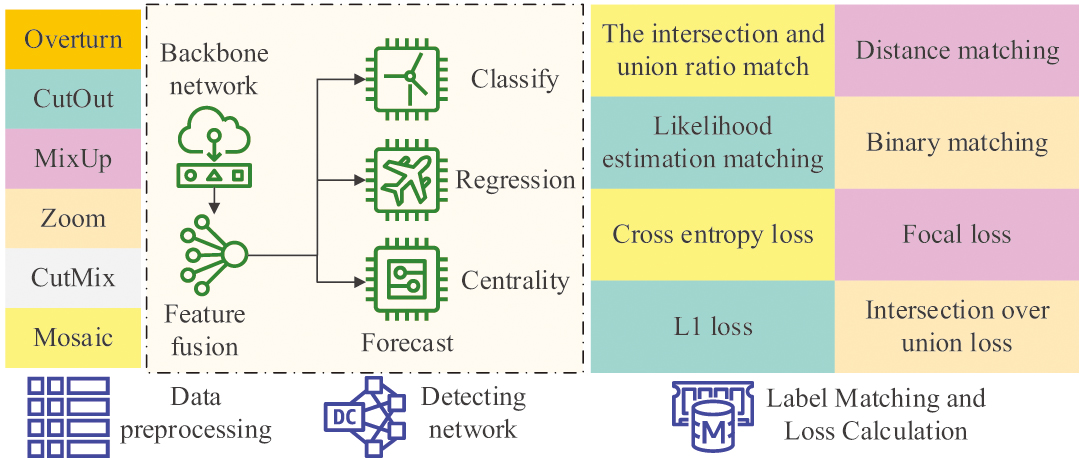Fig. 1. Roadmap of object detection technology.

In Fig. 1, TD roughly consists of three stages: data preprocessing, detection network initialization and feature label matching, and loss function calculation. The basic formula for data preprocessing is given in equation (1):

{Z=(X−μ)/σθ=(X−min(X))/(max(X)−min(X))Y=X/10∧pY′=X/‖X‖
where Z represents zero mean normalization standard processing, X represents raw data, μ represents the average of the original data, σ represents the standard deviation of the original data, θ represents standardization of dispersion, min(X) represents the minimum value of the original data, max(X) represents the maximum value of the raw data, Y represents the standardization of decimal scaling, p represents the exponent suitable for the operation, Y′ represents normalized standard processing, and ‖X‖ represents the norm of the raw data. In data preprocessing, errors are mainly used to evaluate the prediction results. The error between its absolute and relative values is shown in equation (2):
{E=U−U^E′=(U−U^)/U∗100%
where E represents absolute error, U represents the true value, U^ represents the predicted value, and E′ represents relative error. The prediction effect can be evaluated most directly through absolute and relative errors. In addition, the definitions of mean square error and mean square error are shown in equation (3):
{MAE=1/n∑i=1n|Ei|=1/n∑i=1n|Ui−U^i|MSE=1/n∑i=1nEi2=1/n∑i=1n(Ui−U^i)2
where MAE represents the average absolute error, n represents the total number of targets, and i represents the image sequence number. MSE represents the mean square error. The average absolute error can avoid mutual cancelation between positive and negative parameters. The mean square errors can directly add up the positive and negative errors, and it improves the sensitivity of this indicator by squared. In addition, the mathematical expressions of root mean square error and mean absolute percentage error are shown in equation (4):
{RMSE=(1/n∑i=1nEi2)1/2=(1/n∑i=1n(Ui−U^i)2)1/2MAPE=1/n∑i=1n|Ei/Ui|=1/n∑i=1n|(Ui−U^i)/Ui|
where RMSE represents the root mean square error and MAPE represents the average absolute percentage error. The value of root mean square error can provide feedback on the dispersion of the predicted value. When the average absolute percentage error is less than 10, effective information with high prediction accuracy can be fed back. In addition, the mathematical expression of the linear regression function is shown in equation (5):
{α(x)j=exj/∑k=1kexk,j=1,..,kfβ(xi)=[eβ0Txieβ1Txi…eβk−1Txi]/∑j=0k−1eβjTxi
where x represents the vector value, α() represents a dimensional vector, e represents a natural constant, k represents the maximum value of the dimension, j represents the current dimension, β represents the pending parameter, and f() represents the probability function. T represents the temperature coefficient for adjusting the smoothness of the curve. Linear regression functions can better predict discrete results and accurately classify them according to different weights. The expression equation similar to the cross-entropy loss function in the last step is shown in equation (6):
H(p,q)=−∑i=1Np(xi)logq(xi)
where H represents the cross-entropy of the cost function, p represents the true distribution probability, q represents the probability of fitting the distribution, x represents the sample space, and N represents the variable coefficient. The most frequently used image recognition and classification network is CNNs. The model is shown in Fig. 2 [24,25].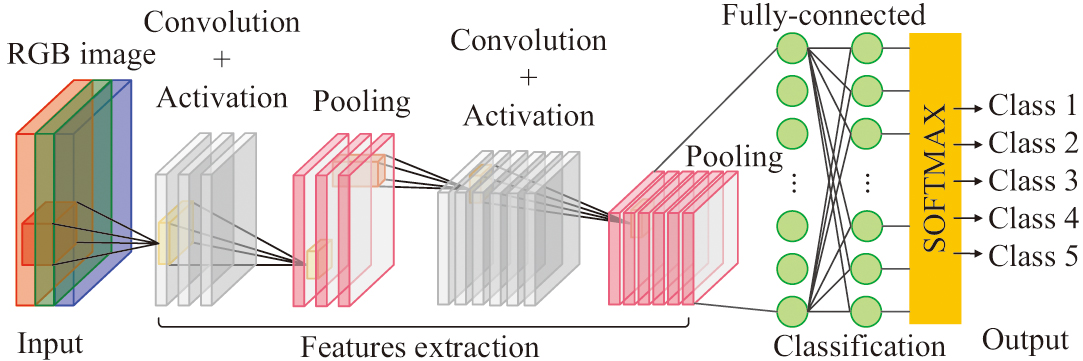

Fig. 2. Simulation of a convolutional neural network.

In Fig. 2, CNN is mainly composed of four parts. The first part is the input layer, which consists of the input layer responsible for collecting visual information from the physical world. The second part is the feature extraction layer, which consists of multiple convolutional layers and pooling layers for feature extraction based on real-time input visual information. The third part is the classification layer composed of multiple neurons with certain classification ability and multiple classification activation functions. The fourth part is the output layer responsible for outputting effective classification results of image information. The data need to be normalized in the CNN calculation process. Its mathematical expression is shown in equation (7):

{μ←∑i=1mxi/m∂2←∑i=1m(xi−μ)2/mx^i←(xi−μ)/∂2+ɛyi←γx^i+β≡BNγ,β(xi)
where μ represents the average value of a single set of data, ∂2 represents the variance of a single set of data, x^i represents the whitening treatment result for underexposed or overexposed images, yi represents the data processing result, ɛ represents the error coefficient, i represents the image sequence number, and m represents the total number of images. Both γ and β represent random parameters. BN represents the normalization function. In addition, CNN can combine multiple activation functions to form abstract functions for multitasking classification of complex videos or images. The activation function formula is shown in equation (8):
{Sigmoid(x)=1/(1+e−x)tanh(x)=sinh(x)/cosh(x)=(ex−e−x)/(ex+e−x)

In equation (8), Sigmoid represents the activation function of the growth curve, tanh represents the hyperbolic tangent activation function, sinh represents a hyperbolic sine function, and cosh represents a hyperbolic cosine function. In order for the seal cutting robot to better perform humanoid manual seal cutting, it is necessary to increase the differences between seal recognition elements. Therefore, local feature fusion (LFF) is added to the classification model to improve the accuracy of biomimetic seal cutting. The feature fusion network structure is shown in Fig. 3 [26,27].

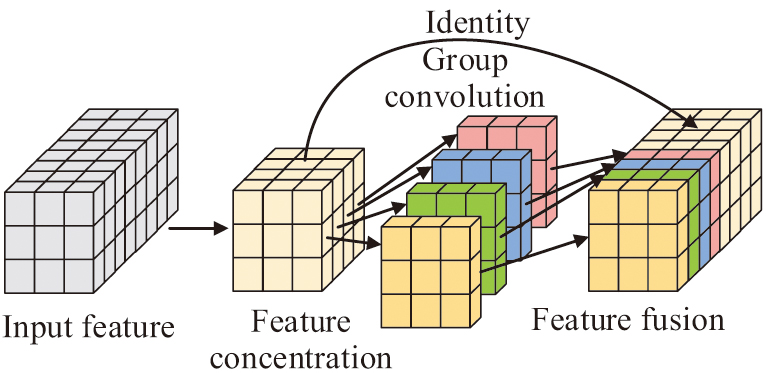Fig. 3. Structure diagram of feature fusion classification network.

In Fig. 3, the feature fusion classification network performs three steps for input features: feature concentration, group convolution feature extraction, and feature fusion. The final model combines global and local features to obtain seal data features that contain both abstract global semantic information and local semantic details. This enables robots to more accurately imitate humans for seal carving. Moreover, the system can store high-precision seal images and feature data in a database to provide customers with a rich selection of models or patterns.

B.SIMULATION AND IMPLEMENTATION OF SEAL RECOGNITION AND CUTTING ROBOT BASED ON REINFORCEMENT LEARNING

Before starting seal cutting, not only should the target seal be identified and analyzed, but also the recognized patterns of various types of seals should be mapped to the material surface to form a three-dimensional seal image. The purpose is to provide a reference model and original blank for the next step of dynamic simulation. In research, reinforcement learning is used as an autonomous learning method to enable seal engraving robots to learn the optimal seal engraving strategy during interaction with the environment. By constantly trying and adjusting actions, robots can gradually learn how to achieve efficient and accurate seal carving in different scenarios guided by constantly receiving reward signals. This study introduces the PCM to represent the data structure of three-dimensional seals. PCM can be composed of a large number of three-dimensional coordinate points sufficient to depict seal details without a network structure [28]. To ensure the authenticity of seal cutting, it is necessary to convert the selected 2D seal image into a depth map that can be projected onto a PCM. The specific system design is shown in Fig. 4.

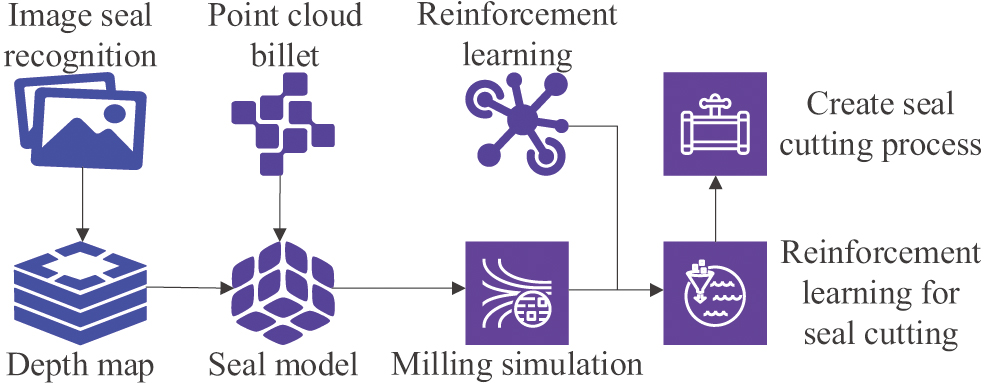Fig. 4. Technical roadmap of seal cutting process generation system.

In Fig. 4, the system first searches and filters the desired seal-type image of the customer or recognizes the photo and then performs joint analysis with the image in the database to convert it into a depth map. The depth projection process of the PCM is shown in Fig. 5.

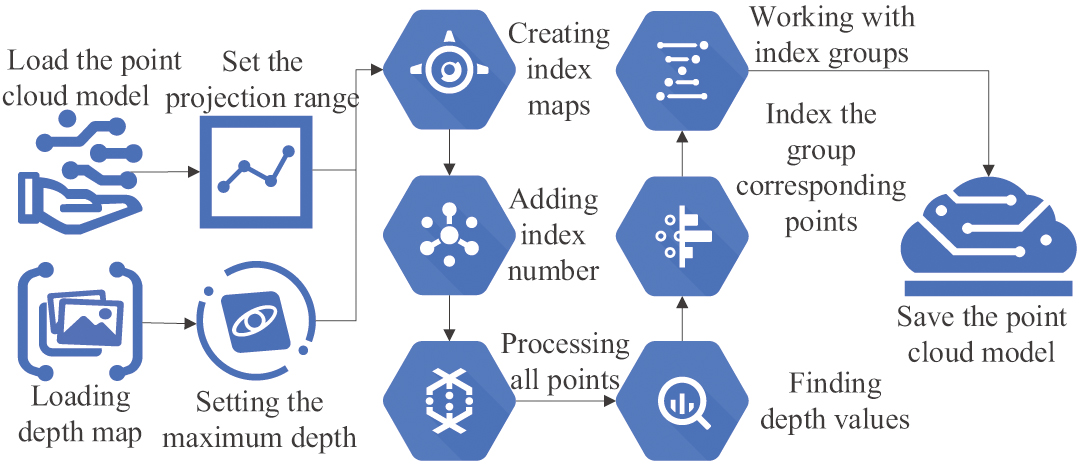Fig. 5. Flow chart of depth projection of point cloud model.

In Fig. 5, projecting the image depth onto the PCM includes three steps: loading, processing all points of the PCM, and processing all index groups in the index map. This study introduces the Deep Deterministic Policy Gradient (DDPG) algorithm for system control of continuous actions in space. The mathematical expression of its strategy and value function network update is shown in equation (9):

{θ′_π′=argmaxθ′_πJ(θ′_π)θ′_Q'=argminθ′_QL(θ′_Q)
where θ′_π′ represents the updated policy network parameters, θ′_Q' represents the updated value function network parameters, J(θ′_π) represents the objective function of the policy network, L(θ′_Q) represents the value function network loss function, θ′_π represents the current policy network parameters, and θ′_Q  represents the current value function network parameter. The target strategy network and value function network update parameters and explore the mathematical expression of noise as shown in equation (10);
{θ′_π' = τ′ * θ′_π + (1 − τ′) * θ′_π'θ′_Q' = τ′ * θ′_Q + (1 − τ′) * θ′_Q'a' = π(s'|θ′_mπ') + N′
where θ′_mπ' represents the target policy network parameters, θ′_mQ' represents the network parameter of the objective value function, a' represents action, π represents strategy, s' represents the state, τ' represents a small constant, and N′ represents noise. The extremely subtle changes in hyperparameters can also cause significant fluctuations in DDPG. Therefore, the study further introduces the Proximal Policy Optimization (PPO) algorithm, which uses the Actor-Critic (AC) framework to deeply sample and optimize the objective function in the natural environment. PPO will use small-scale operations to update each objective function at different times. The mathematical expression of its advantage estimation is shown in equation (11):
A′(s′,a′) = Q′(s′,a′) − V′(s′)
where A′ represents the advantage value, Q′ represents the value function of a certain action in a certain state, and V′ represents the value function in a certain state. By using this formula, the degree of advantage of a certain action compared to the average value in a certain state can be evaluated. The definition of its alternative objective function is shown in equation (12):
L(θ)=E[min(ratio*A′(s,a),clip(ratio,1−τ',1+τ')*A′(s,a))]
where L(θ) represents the objective function, E represents the expected values for all actions in all states, and ratio represents the proportion of new and old strategies. The strategy update and value function update are shown in equation (13):
{θ_new = argmaxθ′ L_clip(θ)V_new(s) = E[R + γV(s')]
where θ_new represents the updated policy parameters, L_clip(θ) represents the objective function of the cut, V_new(s) represents the updated value function estimation, θ′ represents the policy parameter, R′ represents a return, γ represents the discount factor, and V(s') represents the estimation of the value function for the next state. The definition of its shear value function objective is shown in equation (14):
Lvf(θ)=E[(V(s)−Vtarget(s))2]

In equation (14), Lvf(θ) represents the loss function of the value function and V(s) represents the value function estimation of the current state. Vtarget(s) represents the estimation of the objective value function. When the differences between strategies are too large, the action control of the PPO algorithm will lose its advantage and fall into a local optimal solution. Therefore, this study introduces the Soft-Actor-Critic (SAC) algorithm by maximizing the entropy of the strategy while optimizing the overall strategy. The mathematical expression of its target strategy is shown in equation (15):

πMaxEnt∗=argmaxπ∑tE(st,at)∼ρπ[r(st,at)+α′H(π(·|st))]
where ρπ represents the distribution of state actions under policy control, α′ represents the hyperparameter of the temperature coefficient, and H represents an update. SAC can reasonably regulate the randomness of the target entropy so that the robot can fully explore all possibilities without falling into a local optimal solution. The basic logical loop of interaction and action feedback between intelligent agents and the environment is shown in Fig. 6.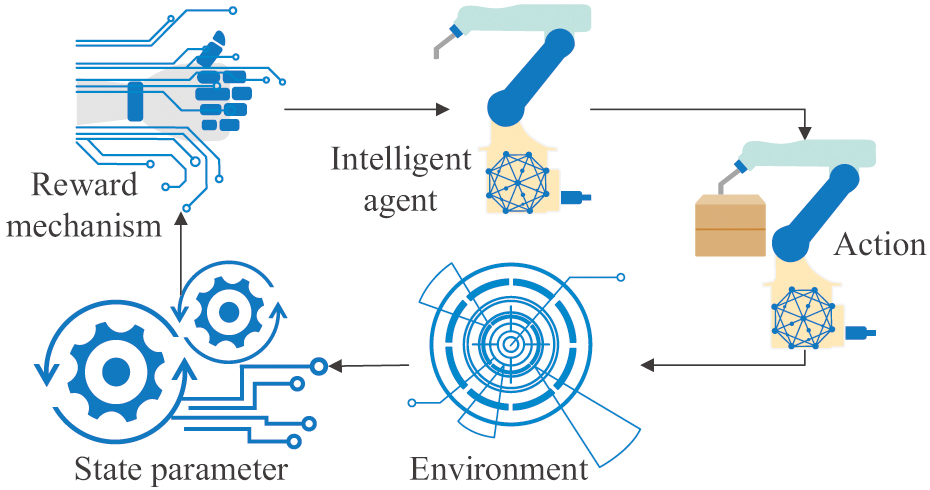

Fig. 6. Illustration of the interaction loop in the agent environment.

From Fig. 6, reinforcement learning mainly consists of the interaction between the agent and the environment. The intelligent agent uses the environmental state parameters transmitted by environmental sensors and the reward mechanism of computer programs as basic parameters to search for the corresponding optimal strategy. It uses intelligent algorithms and executes the optimal action in that state. The degree of proximity between the actual cutting position and the target position during the robot seal cutting process should be measured. The closer the blade is to the target position, the higher the reward value. The time required for robots to complete seal cutting tasks should be measured. On the premise of ensuring the accuracy of seal cutting, the faster the completion speed, the higher the reward value. The degree of fluctuation of robots during the seal cutting process should be measured. The smaller the fluctuation, the more stable the sealing process of the robot, and the higher the reward value. When the robot makes an error during the seal cutting process, such as the carving knife deviating too much from the target position, a negative reward will be given to encourage the robot to avoid similar errors in subsequent learning. The Seal Recognition and Cutting Robot with Reinforcement Learning (SRCR), which integrates TD technology, LFF mechanism, CNN structure, PCM model, DDPG, PPO, and SAC algorithm, is applied to actual seal cutting. From the above content, it can be seen that this method can effectively improve the quality and efficiency of seal engraving.

4.EXPERIMENTAL SIMULATION AND DATA ANALYSIS

To verify the sealing performance of the seal cutting robot SRCR, this study conducted dynamic simulation of seal cutting by detecting real-time changes in the blank and real-time detection of the calculation process. The study uses a PCM for seal cutting simulation. It removes the points that the cutting tool passes through and inserts new points to simulate the process of generating new marks on the cutting head. And research is conducted to establish a new network visualization model by sampling the surface of the cutting tool and the blank, controlling the spatial motion of the cutting tool in the coordinate system to simulate machining. Due to the fact that both the sealing tool and the blank are PCMs, during the sealing process, when the points of the blank model completely coincide with the position of the cutting tool, they are considered as deleted points. The root mean square difference transformation curve and DDPG, PPO, and SAC during seal cutting simulation using the seal cutting method are shown in Fig. 7.

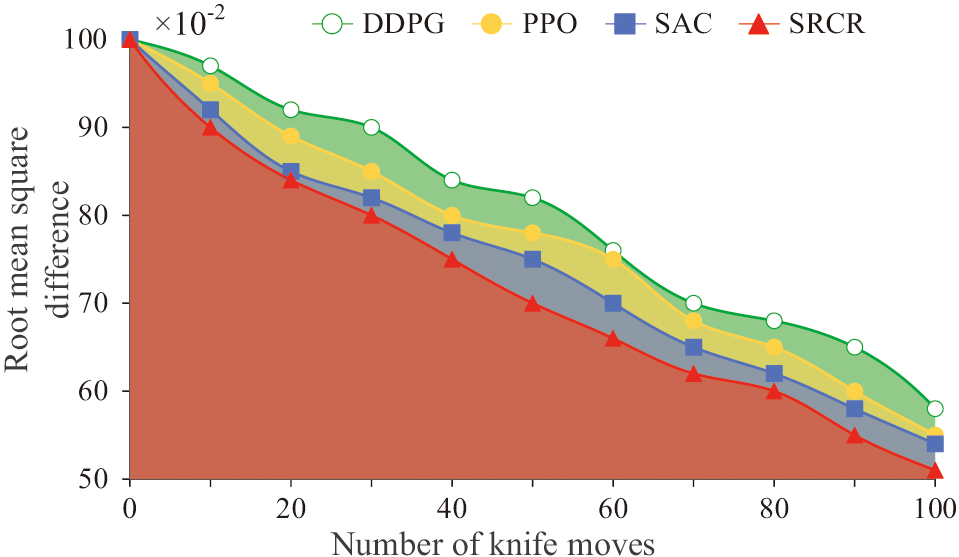Fig. 7. Comparison of root mean square difference changes.

In Fig. 7, the ordinate represents the root mean square difference between the target model surface and the original blank surface, which can express the error between the cutting position point of the engraving tool in seal cutting and the actual model point. The faster the root mean square difference changes, the smaller the difference, indicating a higher seal cutting accuracy. The root mean square difference of SRCR decreases about 1% faster than SAC, about 2% faster than PPO, and about 4% faster than DDPG. This indicates that SRCR has certain advantages in actual accuracy after cutting. The overall monitoring of the four algorithms for tool training is shown in Fig. 8.

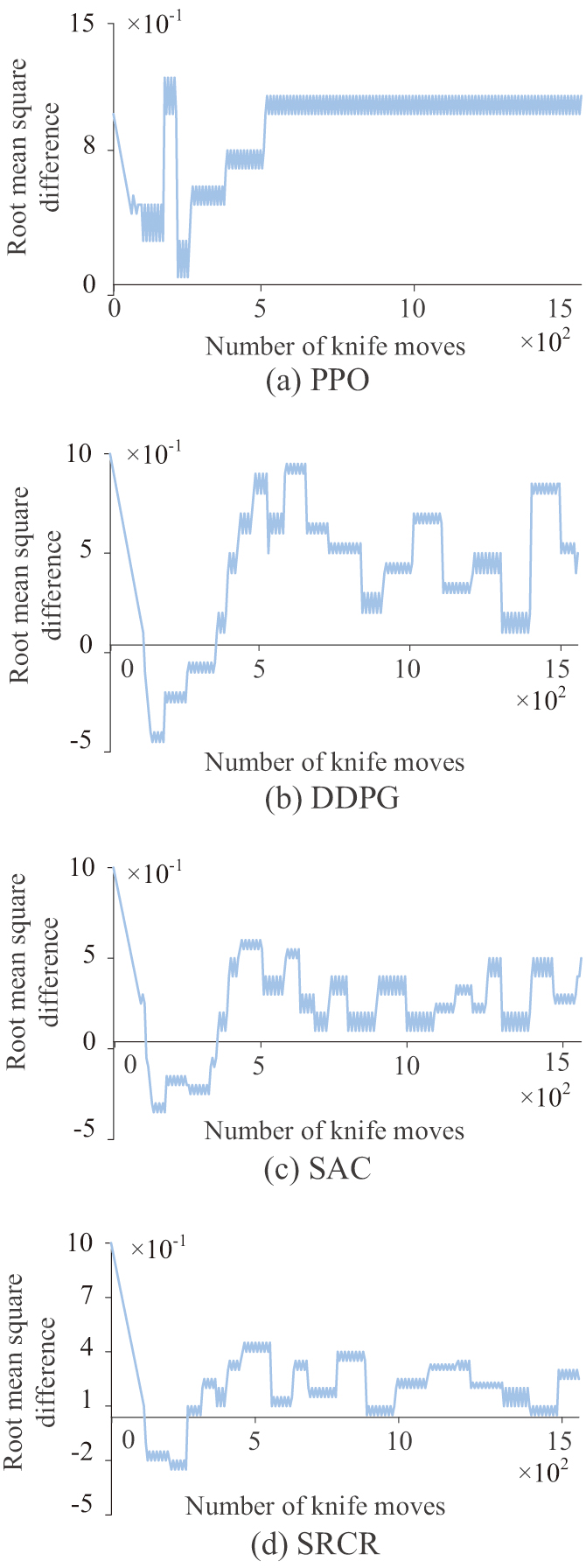Fig. 8. Comparison of root mean square difference monitoring.

If every 100 cuts from a training cycle as shown in Fig. 8, it can be observed that the PPO algorithm begins to fall into a local optimal solution in the fifth training session and cannot be reasonably cut according to the model. DDPG is overly sensitive to hyperparameters, resulting in excessive fluctuations even though it is not trapped in a local optimal solution. The fluctuation of SRCR is about 10% smaller than that of SAC and about 60% smaller than that of DDPG. Therefore, SRCR has the highest overall stability without falling into local optima. This study further verifies the variation law of the overlap degree between the target blank and the original blank under various algorithms. The comparison is shown in Fig. 9.

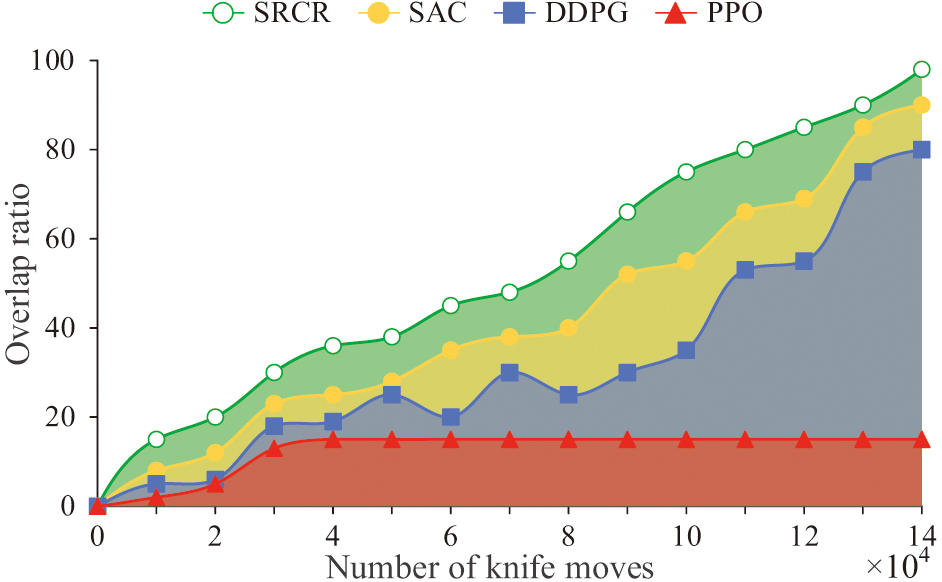Fig. 9. Comparison of coincidence degree.

In Fig. 9, due to the PPO falling into local optima, the coincidence degree is low, about 17%. The fluctuation range of DDPG during the seal cutting process is relatively large, and the overall curve is relatively slow, with a final overlap of about 70%. The overlap of SAC is slightly higher by about 83%. The highest stability of SRCR overlap is best around 90%. To further verify the sealing accuracy of SRCR, it was compared with inception network (IN), DenseNet (DN), and the fusion of IN and DN (INDN), CNN, and convolutional recurrent neural network (CRNN), on 10 datasets containing a large amount of different standard seal information. The results are shown in Fig. 10.

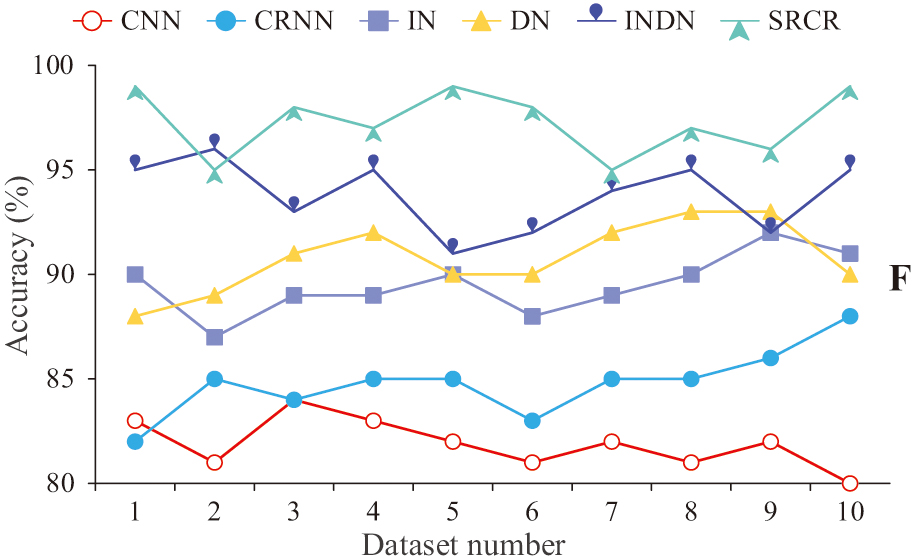Fig. 10 . Comparison of seal recognition efficiency.

In Fig. 10, the average sealing accuracy of SRCR is about 97%. SRCR improves the sealing accuracy by about 4% compared to INDN structure. The seal engraving accuracy of DN structure is about 3% higher than that of IN structure. The seal engraving accuracy of the INDN structure is improved by about 7% compared to traditional deep learning networks. Therefore, SRCR has increased by about 4% compared to INDN, about 5% compared to DN, about 6% compared to IN, about 9% compared to CRNN, and about 15% compared to CNN. This study further conducted comparative tests on the accuracy of multilingual seal feature engraving on SRCR, and the results are shown in Fig. 11.

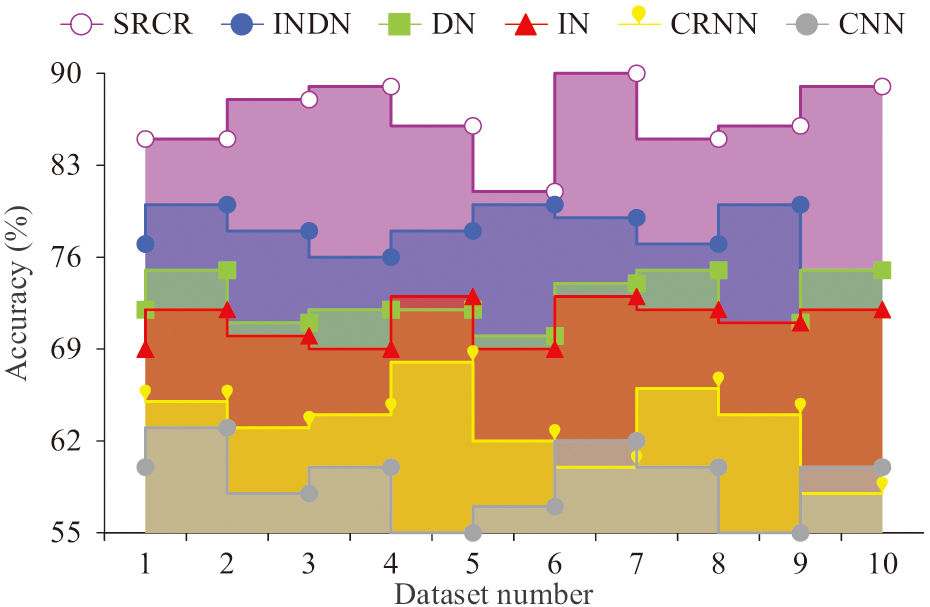Fig. 11. Comparison of multilingual character recognition accuracy.

In Fig. 11, the seal information engraving accuracy of SRCR in a multilingual environment is approximately 88%. INDN is approximately 77%. DN is approximately 72%. The IN is approximately 70%. The CRNN is approximately 63%. CNN is approximately 58%. Although the seal cutting accuracy of SRCR has decreased in multilingual environments, it is still in an advantageous position. Further verification is needed to verify the sealing accuracy of SRCR in datasets containing a large amount of irregular seal information such as rotating seals, deformed seals, and twisted seals. Therefore, the study used a multi-directional and multi-scale deformation seal dataset to test it. The comparison results are shown in Fig. 12.

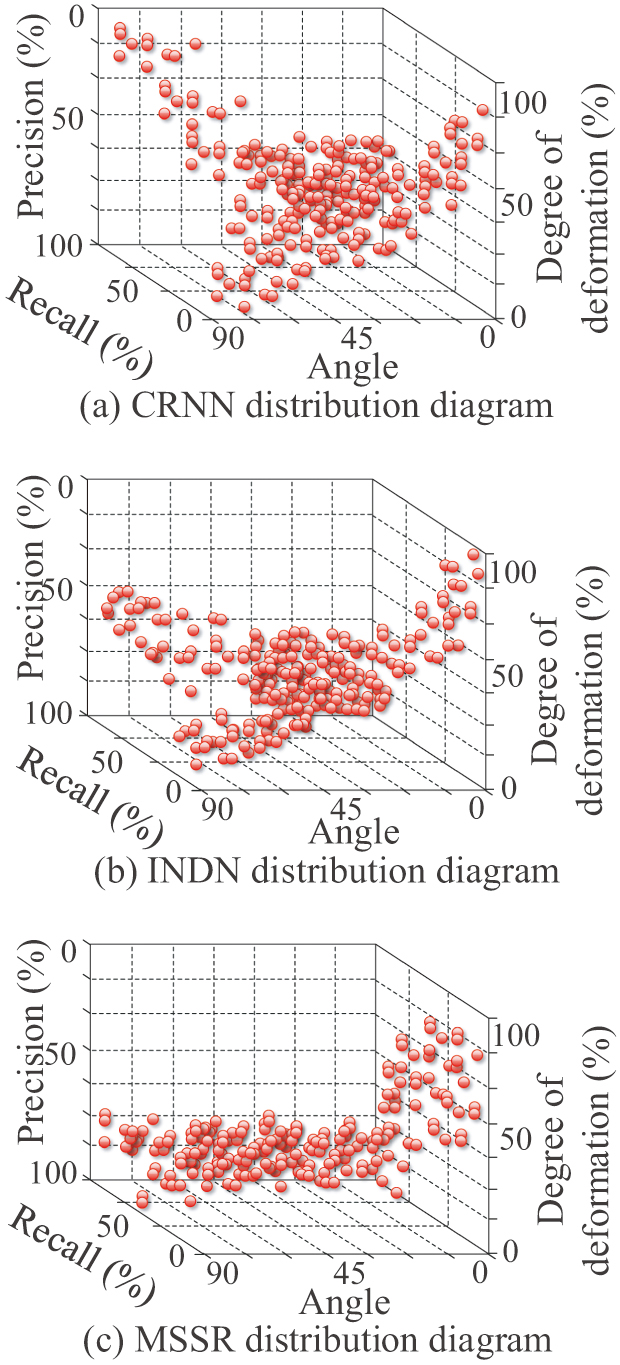Fig. 12. Multi-scale seal recognition rate.

In Fig. 12, the overall probability of SRCR in multi-angle seal image engraving is maintained at about 90%. When the angle increases to 45°, the overall performance decreases to an average of about 85%. The comprehensive seal cutting accuracy at 90° is almost 75%. The comprehensive performance of SRCR in multi-scale deformation seal images is 60% when the deformation rate is 50%. When its deformation reaches 100%, it decreases to 5%. The overall probability of INDN in multiple angles remains at approximately 85%. When it decreases to an average of about 75% at 45°C, it shows a downward trend. The overall efficiency is close to 50% at 90°C. The comprehensive performance of INDN in multi-scale deformation seal images is 50% when the deformation rate is 50% and reduced to 0% when the deformation is 100%. The experimental results indicate that SRCR has certain advantages in indicators such as root mean square difference variation, stability, and overlap. In addition, SRCR has certain advantages in seal cutting testing for various types of seal data information such as standard seals, multilingual seals, and irregular seals.

5.CONCLUSION

This study proposed a seal cutting robot based on reinforcement learning by integrating TD, LFF, CNN, PCM, DDPG, PPO, and SAC for the sealing problem of different types of seal data information. The experiments were conducted to compare and analyze the sealing performance in scenarios such as root mean square difference variation, stability, overlap, multilingual seals, and rotating and deformed seals. The comparison results indicated that the root mean square difference of SRCR decreases about 1% faster than SAC, about 2% faster than PPO, and about 4% faster than DDPG. The data indicated that SRCR had certain advantages in actual accuracy after cutting. The fluctuation of SRCR was about 10% smaller than that of SAC and about 60% smaller than that of DDPG. Therefore, SRCR had the highest overall stability without falling into local optima. The PPO was trapped in local optima, resulting in a low coincidence rate of about 17%. The fluctuation amplitude of DDPG during the seal cutting process was relatively large, and the overall curve was slow, with a final overlap of about 70%. The overlap of SAC was slightly higher by about 83%. The highest stability of SRCR overlap was the best around 90%. In standard seal engraving, SRCR had increased by about 4% compared to INDN, about 5% compared to DN, about 6% compared to IN, about 9% compared to CRNN, and about 15% compared to CNN. The seal information engraving accuracy of SRCR in multilingual environments was about 88%, INDN was about 77%, DN was about 72%, IN was about 70%, CRNN was about 63%, and CNN was about 58%. The above indicates that although the seal cutting accuracy of SRCR had decreased in multilingual environments, it was still in an advantageous position. The experiment fully demonstrated that SRCR had certain advantages in the comprehensive performance of seal cutting in multiple scenarios. However, this model could not further improve performance in scenarios with high computational complexity. And the overall accuracy rate of seal cutting for deformable seals in this model is relatively low. Therefore, further improvement and optimization are needed for the precision of seal cutting in large-scale scenarios and multi-shaped seal changing scenarios.