JAIT

I.INTRODUCTION

At present, unmanned aerial vehicles (UAVs) are widely used in military applications, such as reconnaissance, attack [1], and jamming. Due to the complexity and variability of a battlefield, future UAVs need to be capable of undertaking autonomous operations. Therefore, maneuvering decision-making algorithm of UAV in a combat process of modern air war has become a popular research subject [2]. Artificial rule algorithms [3 –5] and heuristic search algorithms [2] perform well in the field of UAV path planning and UAV maneuvering decision-making, but they cannot be applied to unknown environment. The traditional rule evolution UAV maneuvering decision-making method based on genetic algorithm or genetic fuzzy system relies on human prior knowledge and significantly lacks self-learning ability. UAV decision-making algorithms based on the above algorithms cannot make real-time decisions, so they lack the ability to adapt to unknown environments.

As an important paradigm in artificial intelligence, deep reinforcement learning has shown great advantages in solving various problems and has emerged in many applications in the field of UAV air combat maneuvering decision as well. Part of the research [6,7] combines deep reinforcement learning with traditional methods to make UAV maneuvering decisions, such as Game Theory [6] and Particle Swarm Optimization [7]. However, traditional methods such as Game Theory need to establish a clear and complete problem model. In another part of the research [8 –17], the UAV maneuvering decision-making is realized by deep reinforcement learning, the autonomous maneuvering model of UAV is established by Markov Decision Process (MDP), and the decision function is fitted by neural network. Through training, UAV can master the optimal behavior strategy by the interaction with the environment. However, the existing research of UAV intelligent maneuvering decision based on deep reinforcement learning still has the following shortcomings: (1) the simulation environment is mainly in two-dimensional (3D) space [18], so it lacks high-level exploration and analysis [3] and (2) it does not consider the impact of radar and weapon on air combat, and therefore, it is difficult to apply to a complex battlefield environment.

In response to the above problems, this paper establishes a 3D UAV air combat model, and a UAV maneuvering decision algorithm based on deep reinforcement learning is proposed. The remainder of this paper is organized as follows. In Section I, a UAV air combat model based on the characteristics of the 3D environment is defined. In Section II, intelligent UAV maneuvering decision-making algorithm based on deep reinforcement learning is proposed. In Section III, the simulation results demonstrate the effectiveness of the proposed algorithm in the field of air combat decision, and the simulation results of the Deep Deterministic Policy Gradient (DDPG) algorithm and Twin Delayed Deep Deterministic Policy Gradient (TD3) algorithm are compared. Finally, conclusions are presented in Section IV.

At present, researches on UAV maneuvering decision-making are mostly based on DDPG algorithm [9,18]; therefore, the proposed UAV maneuvering decision-making algorithm based on TD3 is compared with DDPG algorithm.

II.UAV AIR COMBAT MODEL

The following assumptions [9,19] are made for the establishment of the UAV motion and dynamics model:

•Assume that the UAV is a rigid body;
•Ignore the influence of the earth’s rotation and revolution and ignore the earth’s curvature; and
•Due to the large range of maneuverability and short combat time in close air combat, the impact of fuel consumption on quality and the effect of wind are ignored.

In a 3D space, UAV has physical descriptions such as position, speed, and attitude. The 3D space coordinate system where UAV is located is defined as OXYZ, the positive direction of the X axis is north, the positive direction of the Z axis is east, and the positive direction of Y axis is vertical up.

The UAV is regarded as mass point when observing the movement of it. According to the principle of integration, the motion equation of the UAV with three degrees of freedom is shown in Eq. (1). Limited by UAV’s throttle and overload performance, the maneuvering process of UAV in 3D space can be realized by setting suitable $v$ , $a$ , $θ'$ , and $ϕ'$ . The symbols in the equations are explained in Table I.

{\begin{cases} \frac{d X}{d t} = v \cdot \cos θ \cdot \cos ϕ \\ \frac{d Y}{d t} = v \cdot \sin θ \\ \frac{d X}{d t} = v \cdot \cos θ \cdot \sin ϕ \\ \frac{d v}{d t} = a \\ \frac{d θ}{d t} = θ' \\ \frac{d ϕ}{d t} = ϕ' \end{cases}

(1)

where

[X, Y, Z]

represents the position of the UAV in the coordinate system;

v

represents the speed of UAV;

θ

represents the pitch angle of UAV, ranged from

[- 90 °, 90 °]

;

ϕ

represents the heading angle of UAV, ranged from

[- 180 °, 180 °]

;

d t

represents integration step;

a

represents UAV acceleration;

θ'

represents UAV pitch angle variation; and

ϕ'

represents UAV heading angle variation.

TABLE I. Symbols in the equations

Symbol	Meaning
$[X, Y, Z]$	The position of the UAV
$v$	The speed of UAV
$θ$	The pitch angle of UAV
$ϕ$	The heading angle of UAV
$d$	The distance between our UAV and enemy UAV
$q$	Relative azimuth
$D_{\max}$	Missile’s maximum attack distance
$D_{\min}$	Missile’s minimum attack distance
$q_{\max}$	Missile’s maximum off-axis launch angle
$θ'$	UAV pitch angle variation
$ϕ'$	UAV heading angle variation
$V$	The speed vector of UAV
$R$	The position vector of UAV
$V_{m}$	The speed vector of enemy UAV
$R_{m}$	The position vector of enemy UAV
$D$	The relative position vector between our UAV and enemy UAV

The two sides in the battle are modeled in the OXYZ coordinate system. As shown in Fig. 1, $O$ represents the position of our side in 3D space, and $M$ represents the position of the enemy side. Our situation information includes the speed vector of UAV $V = (v_{x}, v_{y}, v_{z})$ , the position vector of UAV $R = (X, Y, Z)$ , pitch angle $θ$ , heading angle $ϕ$ , and the speed of UAV $v$ . Enemy situation information includes the speed vector of UAV $V_{m} = (v_{m x}, v_{m y}, v_{m z})$ , the position vector of UAV $R_{m} = (X_{m}, Y_{m}, Z_{m})$ , pitch angle $θ_{m}$ , heading angle $ϕ_{m}$ , and the speed of UAV $v_{m}$ . The relative position vector between our UAV and enemy UAV is $D$ ; the direction of relative position vector is from our side to the enemy. The distance between our UAV and enemy UAV is $d$ . The angle of $V$ and $D$ is relative azimuth $q$ .

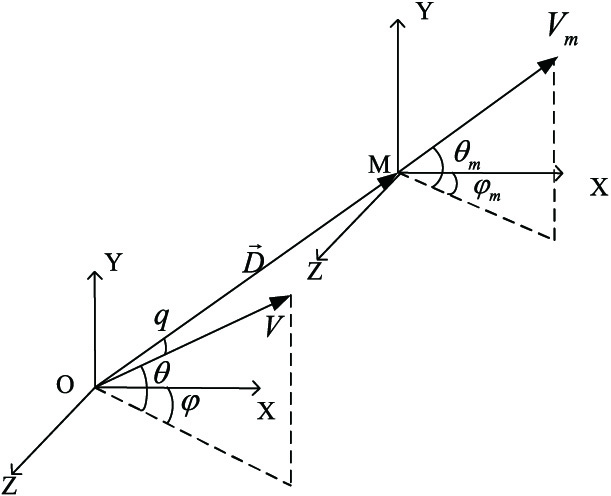Fig. 1. Air combat confrontation situation map.

Therefore, the combat situation of enemy and mine can be described by $D$ , $d$ , and $q$ . The mathematical description of $\vec{D}$ , $d$ _, and $q$ is shown in Eq. (2) to Eq. (4).

D = R_{m} - R

(2)

d = ‖ D ‖

(3)

q = \arccos = (\frac{D \times V}{‖ D ‖ \cdot ‖ V ‖})

(4)

III.INTELLIGENT UAV MANEUVERING DECISION-MAKING ALGORITHM BASED ON DEEP REINFORCEMENT LEARNING

A.TASK SPECIFICATION

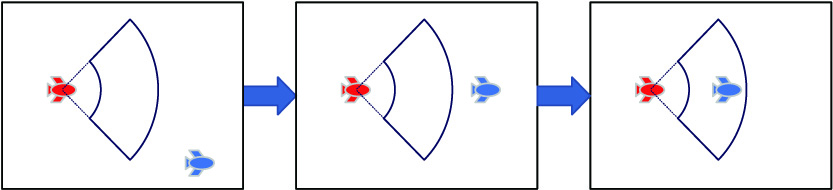
In air combat, the maneuvering decision-making of UAV plays a significant role in the combat result. After initializing the positions of the UAVs on both sides of the battle, the UAV can automatically generate maneuvering decision according to the battlefield situation information based on the deep reinforcement learning algorithm, so that it can occupy a favorable position in the air combat. In consequence, the lock-in and preemptive attack on the enemy has been realized. The combat process is shown in Fig. 2. After the UAV detects the target, it makes a maneuver decision to make the enemy UAV enter the attack area.

Fig. 2. The combat process.

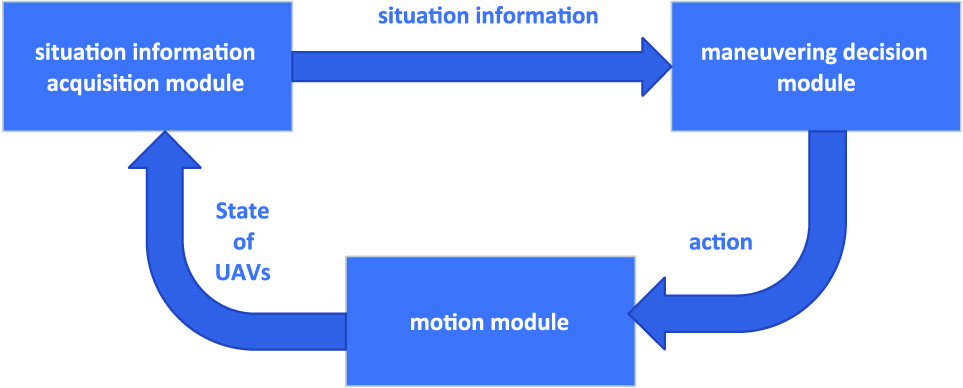
The combat environment in this paper includes UAVs on both sides of the battle. The entire combat process is divided into three parts: the situation information acquisition module of both sides, the maneuvering decision module based on the deep reinforcement learning algorithm, and the motion module. Among them, the situation information acquisition module of both sides calculates situation information and provides it to the decision module for decision-making; the maneuvering decision module generates maneuvering control quantity based on deep reinforcement learning algorithm and provides it for the motion module used to our UAV maneuvering; the motion module updates our position information through the motion equations of UAV, realizes maneuvering, and provides information to the situation information acquisition module of both sides for calculating the corresponding situation. The interaction of the three modules is shown in Fig. 3.

Fig. 3. The interaction process in UAV.

B.RELATED THEORY

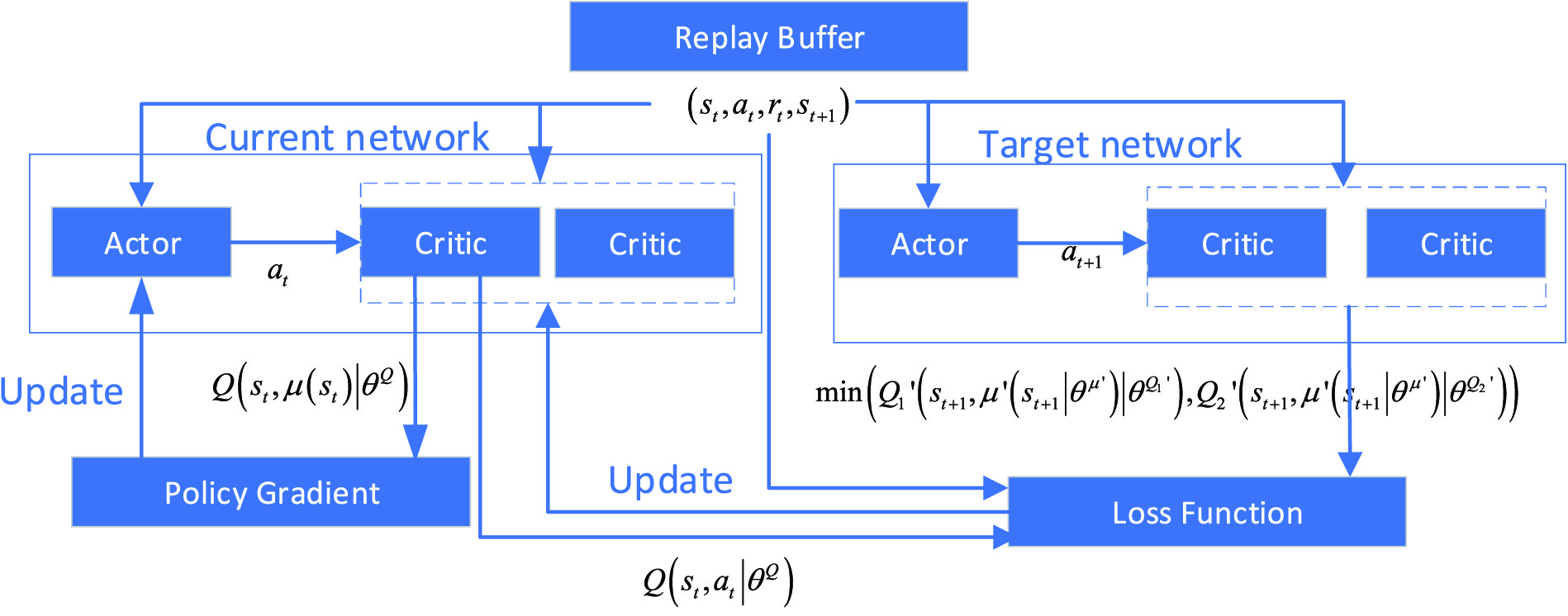
TD3 [20] algorithm is an Actor–Critic algorithm that can operate over continuous action spaces. DDPG [21] algorithm is the theoretical basis of TD3 algorithm. DDPG is an Actor–Critic, model-free algorithm based on deterministic policy gradient that can operate over continuous action spaces. However, there is a shortcoming in DDPG algorithm that the estimated value function is larger than the true value function. To solve this problem, TD3 algorithm improves policy network and value network on the basis of DDPG algorithm, which makes TD3 algorithm perform better than DDPG in many continuous control tasks. The structure of TD3 is shown in Fig. 4.

Fig. 4. The structure of TD3.

Two sets of Critic networks $Q_{θ_{1}}$ , $Q_{θ_{2}}$ are used to calculate different $Q$ in TD3 algorithm. And the minimum $Q$ of the two networks is selected to calculate the target $Q$ , thereby suppressing continuous overestimation. As same as DDPG, Actor network $π_{ϕ}$ is used to output action. Therefore, there are three sets of six neural networks in TD3 algorithm, including two Actor networks and four Critic networks. After the Critic network has been updated many times, the Actor network is updated. The delay of parameter update is to allow the Actor network to make action decisions after the Critic network is not overrated.

Select action with exploration noise is shown as follows:

a \sim π_{ϕ} (s) + ϵ

(5)

where

ϵ \sim N (0, σ)

The calculation formula of target Q is as follows:

Q^{'} (s_{t + 1}, a_{t}) = \min ({Q^{'}}_{1} (s_{t + 1}, a_{t}), {Q^{'}}_{2} (s_{t + 1}, a_{t}))

(6)

The Critic network is updated by calculating the loss function of the Critic network. The loss function is shown as follows:

L o s s_{1} = \frac{1}{N} \sum_{i} {((r_{i} + γ Q^{'} (s_{t + 1}, a_{t})) - Q_{1} (s_{t}, a_{t}))}^{2} L o s s_{2} = \frac{1}{N} \sum_{i} {((r_{i} + γ Q^{'} (s_{t + 1}, a_{t})) - Q_{2} (s_{t}, a_{t}))}^{2}

(7)

The Actor network is updated by policy gradient as follows:

\nabla_{ϕ} J (ϕ) = \frac{1}{N} \sum \nabla_{a} Q (s, a) | a = π_{ϕ} (s) \nabla_{ϕ} π_{ϕ} (s)

(8)

The target networks are updated as follows:

{\begin{cases} {θ_{i}}^{'} \leftarrow τ θ_{i} + (1 - τ) {θ_{i}}^{'} \\ {ϕ_{i}}^{'} \leftarrow τ ϕ_{i} + (1 - τ) {ϕ_{i}}^{'} . \end{cases}

(9)

C.UAV MANEUVERING DECISION-MAKING ALGORITHM BASED ON DEEP REINFORCEMENT LEARNING

MDP can be used to model RL problems. This model describes the relationship among the state, action, and return of the agent in the environment. In this section, based on the MDP, a model is established for the UAV maneuvering decision-making in the air combat process, and the state space, action space, and reward function are defined. Finally, the algorithm flow is introduced.

1)THE DESIGN OF ACTION SPACE AND STATE SPACE

The UAV makes maneuvering decisions based on the situation data and executes maneuvers after obtaining the maneuvering decisions, so that the enemy enters its own missile attack envelop to complete the combat mission. The area where the target that will be hit when the air-to-air missile is launched is also called the missile attack envelop. The missile attack envelop is determined by the air-to-air missile’s maximum firing range $D_{\max}$ , minimum firing range $D_{\min}$ , and maximum off-axis launch angle $q_{\max}$ [21]. Therefore, the state space includes the UAV’s own information and the enemy information that can be obtained, and the action space is the control quantity of the UAV’s actions.

According to Eq. (1) to Eq. (4), the state space of this paper is described by a tuple including eight elements and expressed in a vector as follows:

[X, Y, Z, v, θ, ϕ, d, q]

(10)

where

X, Y, Z

, respectively, represent the position of our UAV on the three coordinate axes, v represents the speed of our UAV

θ

represents the pitch angle of our UAV

ϕ

represents the heading angle of our UAV, d represents the distance between us and the enemy, and q represents the relative azimuth of enemy.

According to Eq. (2) to Eq. (4), it can be seen that the motion of UAV is controlled by acceleration $a$ , pitch angle variation $θ'$ , and heading angle variation $ϕ'$ . Therefore, the action space of UAV can be designed as a tuple including three elements and expressed by a vector as follows:

[a, θ', ϕ']

(11)

2)THE REWARD FUNCTION OF THE AIR COMBAT SITUATION

We need to get enemy UAV into our missile attack envelop to accomplish our mission. The range of missile attack envelop is determined by the air-to-air missile’s maximum attack distance $D_{\max}$ , minimum attack distance $D_{\min}$ , and maximum off-axis launch angle $q_{\max}$ . And air-to-air missiles need a certain enemy lock time $t_{\max}$ before they can be launched.

The time that the enemy has been continuously in our missile attack envelop is $t_{i n}$ . When Eq. (12) is satisfied, it can be considered that our missiles were successfully launched, and the enemy was destroyed by our missiles, and our combat was successful. The reward function in this paper is composed of continuous rewards and sparse rewards. Among them, the continuous reward function is negatively correlated with the relative azimuth and the relative distance. According to Eq. (12), the angle reward and distance reward have been considered in this paper.

{\begin{cases} D_{\min} < D < D_{\max} \\ q < q_{\max} \\ t_{i n} > t_{\max} \end{cases}

(12)

The angle reward $r_{a}$ is shown as follows:

r_{a_{1}} = - q / 180 r_{a_{2}} = {\begin{cases} 3, if q < q_{\max} \\ 0, else \end{cases} r_{a} = r_{a_{1}} + r_{a_{2}}

(13)

The distance reward $r_{d}$ is shown as follows:

r_{d_{1}} = - q / (5 \cdot D_{\max}) r_{d_{1}} = {\begin{cases} 3, if D_{\min} < d < D_{\max} \\ - 1, if d < d_{\min} \end{cases} r_{d} = r_{d_{1}} + r_{d_{1}}

(14)

where

r_{d_{1}}

is continuous reward,

r_{d_{2}}

is sparse reward,

D_{\min}

is minimum attack distance

D_{\max}

is maximum attack distance, and

d

is the distance between us and the enemy.

The reward function is defined as follows:

R = u_{1} * R_{d} + u_{2} * R_{a}

(15)

where

u_{1}, u_{2}

are weight coefficients, and we set

u_{1} = u_{2} = 0.5

3)ALGORITHM PROCEDURE

According to the above definition, the training process of the UAV maneuvering decision-making algorithm based on TD3 is shown in Table II. The complexity of the UAV maneuvering decision-making algorithm based on TD3 is $O (n)$ same as DDPG, but it performs better.

TABLE II. Training process of the UAV maneuvering decision-making algorithm based on TD3

Algorithm TD3
Input: Replay Bufferbatch_size update step dOutput: Model of TD3
1. Initialize Critic networks $Q_{ϕ_{1}}$ , $Q_{ϕ_{2}}$ , and Actor network $π_{θ}$ with random parameters $ϕ_{1}$ , $ϕ_{2}$ , $θ$ .
2. Initialize target network $Q'$ and $μ'$ with weights $θ^{'} \leftarrow θ, ϕ_{1}^{'} \leftarrow ϕ_{1}, ϕ_{2}^{'} \leftarrow ϕ_{2}$
3. Initialize replay buffer $R$
4. FORt = 0n do:
5. Select action with exploration noise $a = π_{θ} (s) + ς$ , where $ς$ obey normal distribution
6. The UAV performs action $a$ , and observes reward $r$ and new state $s^{'}$
7. Store transition $(s, a, r, s')$ in $R$
8. IF the transition storage capacity in $R$ is larger than batch_size:
9. Sample batch_size of transitions $(s, a, r, s')$ from $R$
10. $a^{'} = π_{θ^{'}} (s^{'})$ , $y = r + γ \min (Q_{ϕ_{1}^{'}} (s^{'}, a^{'}), Q_{ϕ_{2}^{'}} (s^{'}, a^{'}))$
11. $l o s s 1 = \sum_{i = 1}^{N} {(Q_{ϕ_{1}} (s, a) - y)}^{2}$ , $l o s s 2 = \sum_{i = 1}^{N} {(Q_{ϕ_{2}} (s, a) - y)}^{2}$
12. Update parameters of Critic network $ϕ_{1}, ϕ_{2}$
13. IFt mod d then
14. $\nabla_{θ} J (θ) = \frac{1}{N} \sum \nabla_{a} Q_{ϕ_{1}} (s, a) \|_{a = π_{θ} (s)} \nabla_{θ} π_{θ} (s)$
15. Update parameters of Actor network $θ$
16. Update target networks:
17. $θ^{'} \leftarrow θ + (1 - τ) θ^{'} {ϕ_{1}}^{'} \leftarrow ϕ + (1 - τ) {ϕ_{1}}^{'} {ϕ_{2}}^{'} \leftarrow ϕ + (1 - τ) {ϕ_{2}}^{'}$
18. END if
19. Skip to step 5, and $s \leftarrow s'$
20. END if
21. END FOR

IV.EXPERIMENT AND ANALYSIS

A.EXPERIMENTAL PARAMETER SETTINGS

1)PARAMETER SETTINGS OF TD3 ALGORITHM

The parameters of TD3 algorithm are shown in Table III, where training round represents the number of training rounds for the network in the algorithm in a certain initial state; the maximum simulation step size indicates the maximum number of actions performed by the agent in a training round, when this number of times is reached, the training of this round is over; the time step represents the time interval for the agent to perform actions; and batch_size represents the number of samples taken from the replay buffer each time during training.

TABLE III. Parameter settings of TD3 algorithm

Parameter	Value
Training round	2000
Maximum simulation step size	800
Time step	0.1
batch_size	256
Discount factor	0.99
Exploration noise	$N (0, 0.2)$
Action bound	[−1,1]
Optimization	Adam
Learning rate of Actor	0.001
Learning rate of Critic	0.0001

2)PARAMETER SETTINGS OF MISSILE AND UAV

The parameters of missile and UAV are shown in Table IV. It is assumed that the target locking time of the missile is 2 s. When the time step is 0.1s, the missile needs to lock the target with 20 simulation steps to launch.

TABLE IV. Parameter settings of missile and UAV

Parameter	Value
Heading angle variation range	6°
Pitch angle variation range	4°
Maximum variation of speed	20 m/s
Maximum speed of UAV	350 m/s
Missile’s maximum attack distance	6 km
Missile’s minimum attack distance	1 km
Maximum off-axis launch angle	30°
Lock time of UAV	2 s

3)THE STRUCTURE OF POLICY NETWORK AND VALUE NETWORK

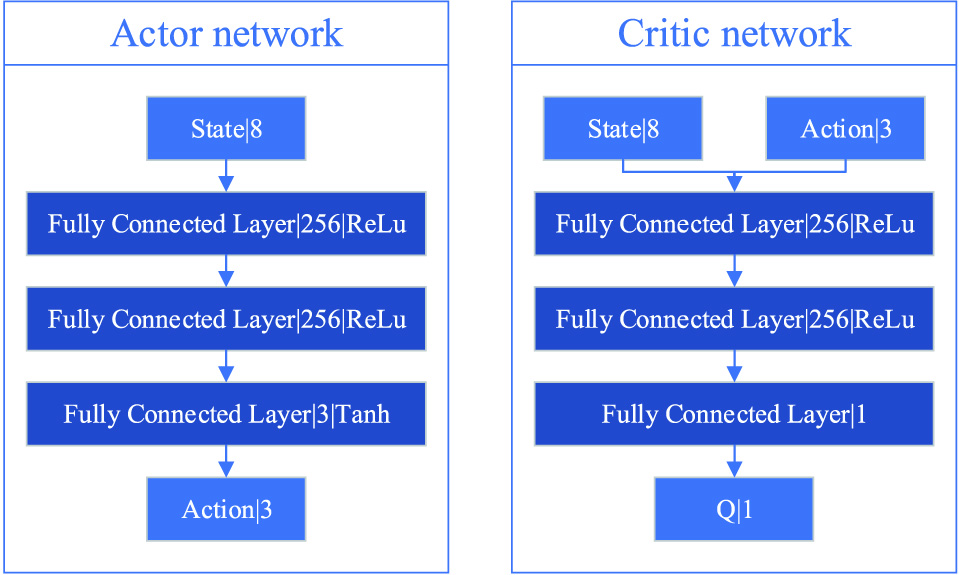
As shown in Fig. 5, the policy network Actor outputs the maneuvering action based on current state. According to the state and action space of UAV maneuvering decision-making, the number of Actor network input nodes is 8, and the number of Actor network output nodes is 3. And since the activation function of output layer is tanh function, the output is limited to [−1,1]. The value network Critic is used to evaluate the value of decision that performs the action in current state. The number of neurons in the input layer and output layer is 11 and 1, respectively. Both Actor and Critic networks are fully connected neural networks with two hidden layers. The number of neurons in the hidden layer is 256, and the activation function is the Relu function.

Fig. 5. The structure of network.

B.SIMULATION EXPERIMENT AND ANALYSIS

In this section, the application of TD3 algorithm and DDPG algorithm in air combat maneuvering decision task is realized by designing relevant experiments, and the efficiency of the algorithm is compared. In the experiment, the red side is an intelligent body that uses deep reinforcement learning algorithms, and the blue side is a non-intelligent body that performs fixed maneuvers. The initial distance between UAVs is 15 km, and the initial relative azimuth is 40°. The parameters and the structure of network of DDPG algorithm are same as TD3 algorithm in Section A.

1)CONVERGENCE SPEED COMPARISON

In order to better evaluate the convergence speed of the algorithm, the total reward obtained by us in each round was recorded during the experiment to determine whether the reward function converges. The change curves of total reward of DDPG algorithm and TD3 algorithm in 4000 training rounds under the same initial conditions are shown in Fig. 6.

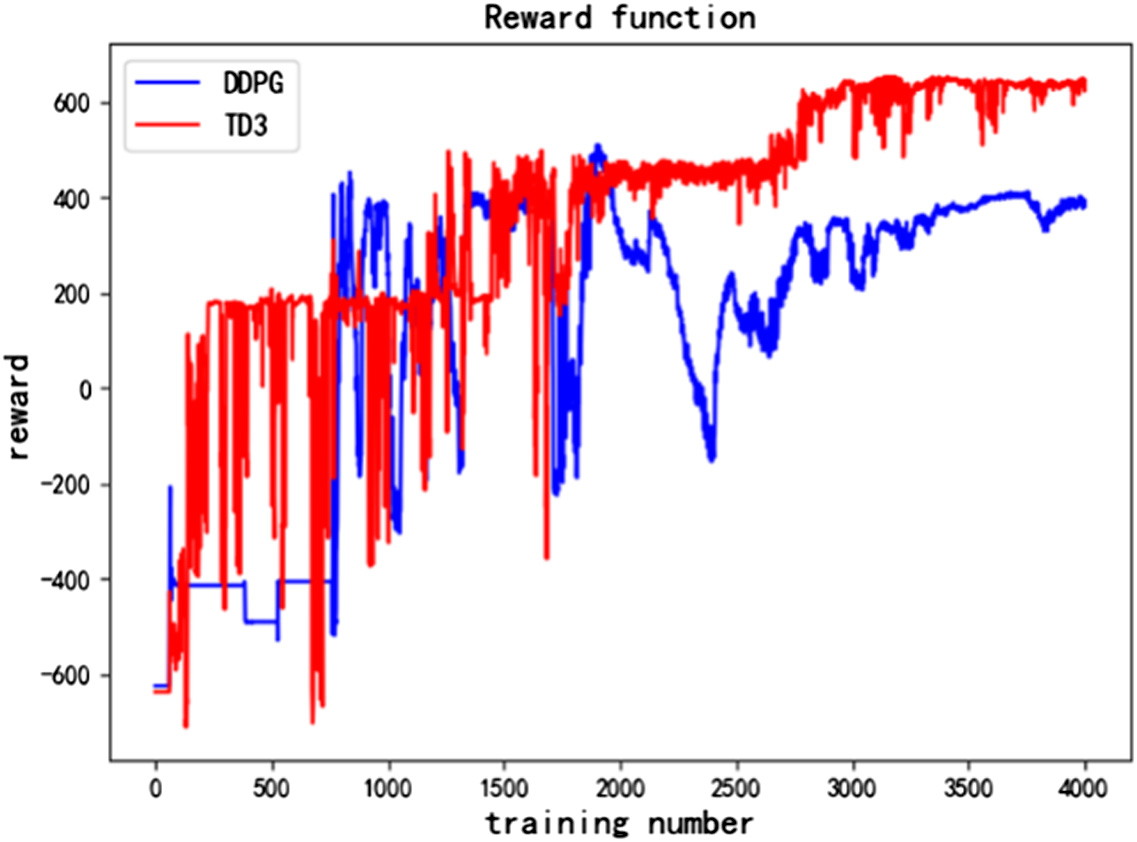Fig. 6. The change curves of total reward.

As shown in Fig. 6, the TD3 algorithm converged locally within 250–2800 rounds and jumps out of local convergence at 2800 rounds to achieve global convergence. The DDPG algorithm reached local convergence in multiple stages and finally did not jump out of local convergence. In the end, the TD3 algorithm converges 200 rounds earlier than the DDPG algorithm, and the maximum reward value that it converges to is greater. At the same time, the DDPG algorithm has a lot of jitter during the convergence process, and the TD3 algorithm is more stable. Therefore, TD3 algorithm has faster training speed and better training results compared with DDPG algorithm.

2)TEST RESULTS COMPARISON

Figs. 7 and 8, respectively, show the combat process of UAV approaching the enemy and meeting launch conditions in different planes.

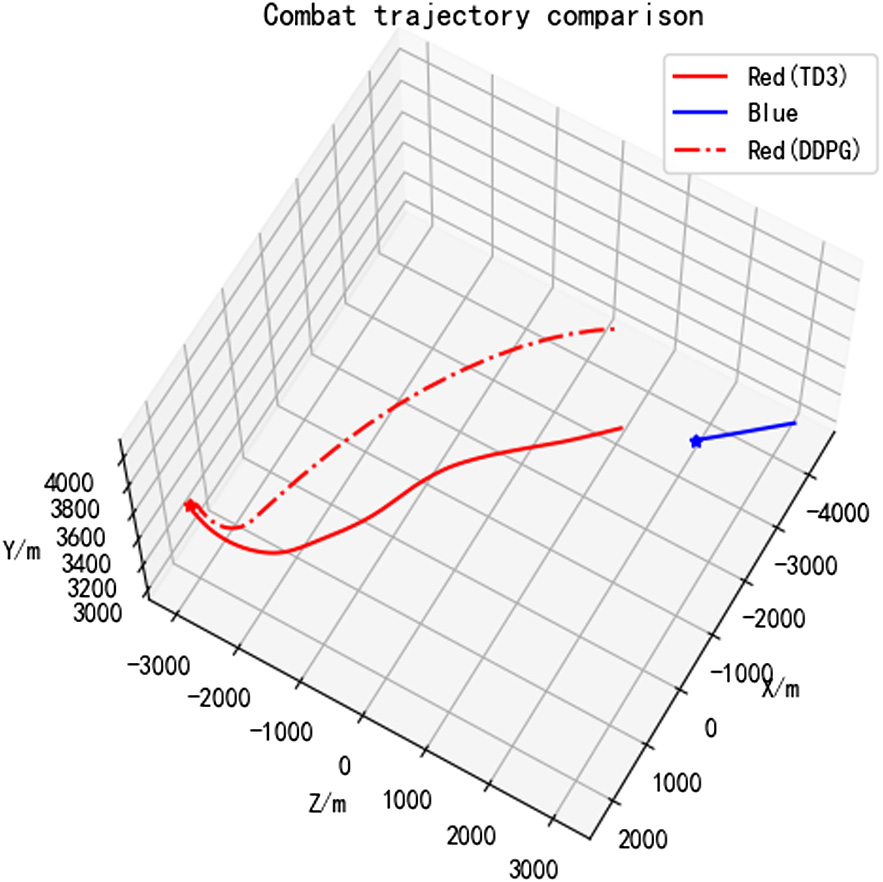Fig. 7. Top view of combat trajectory.

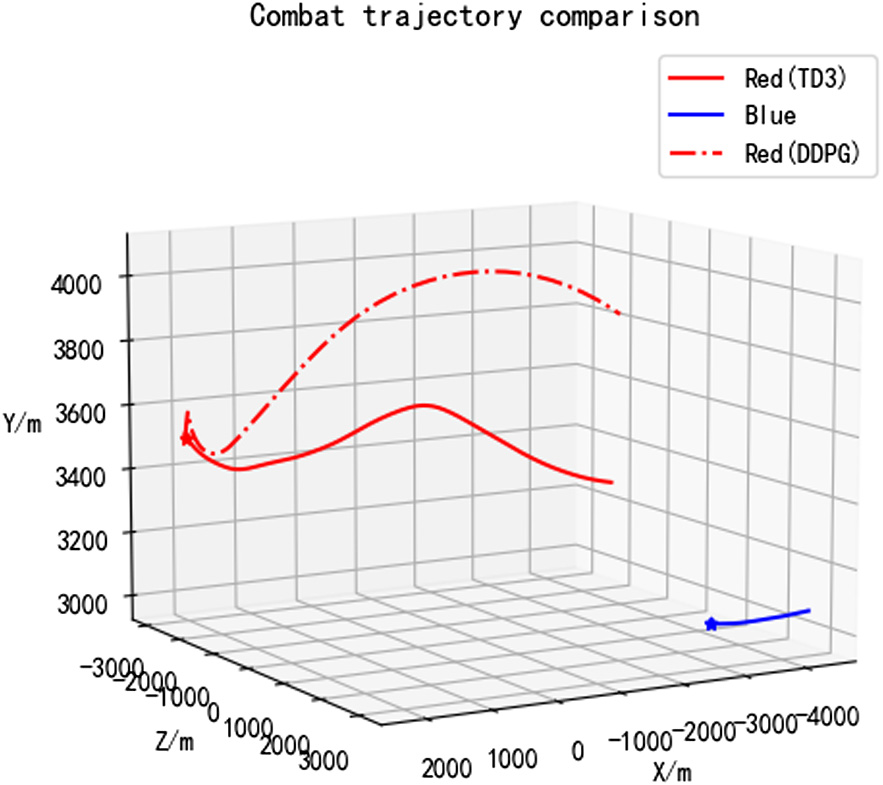Fig. 8. Side view of combat trajectory.

Fig. 7 shows the combat trajectory of the UAV on the horizontal plane. It can be seen from Fig. 7 that after the start of the battle, the blue side with no attack ability moves randomly, and the initial relative azimuth angle and distance of the blue side’s UAV relative to the red side’s UAV are relatively large. In order to make the blue side enter its missile launch area, the red side first quickly changed the heading, reduced the relative azimuth angle, and made a tail-back attack on the blue side.

Fig. 8 shows the altitude change of the UAV during combat. As can be seen from Fig. 8, in the initial state, when the enemy and our side had a height difference and the enemy was lower than us, the red side of TD3 algorithm gradually reduced the height difference during the movement, while the red side of DDPG algorithm always had a large height difference and was always above the enemy’s height.

The decision-making process of the two algorithms is to first change the direction, reduce the relative azimuth angle, and then shorten the distance, and finally reached an attack situation that satisfies the launch conditions. However, by comparing Figs. 7 and 8, it can be seen that the red side turning range in the early stage of the TD3 algorithm is smaller, and the relative azimuth angle is reduced faster. When the launch conditions are finally met, the red side of the TD3 algorithm is closer to the enemy than the DDPG algorithm, and the relative azimuth angle is smaller.

Comprehensive comparison of combat trajectories, compared with the DDPG algorithm, the maneuver strategy generated by the TD3 algorithm can enable the red side to meet the launch conditions more quickly and strike the enemy successfully, which is more suitable for actual combat.

V.CONCLUSION

In this paper, a UAV combat maneuvering decision-making algorithm based on deep reinforcement learning was established. UAV maneuvering model and UAV combat model were established by mathematical algorithm. At the same time, in order to make the battlefield environment more real, the concept of missile attack envelop was introduced in the process of confrontation. Then, this paper realized the UAV air combat maneuvering decision-making based on DDPG and TD3 algorithms. Experimental results show that compared with DDPG algorithm, TD3 algorithm has better convergence speed and optimization ability and is more suitable for solving UAV maneuvering decision problem.

UAV Maneuvering Decision-Making Algorithm Based on Twin Delayed Deep Deterministic Policy Gradient Algorithm

I.INTRODUCTION

II.UAV AIR COMBAT MODEL

III.INTELLIGENT UAV MANEUVERING DECISION-MAKING ALGORITHM BASED ON DEEP REINFORCEMENT LEARNING

A.TASK SPECIFICATION

B.RELATED THEORY

C.UAV MANEUVERING DECISION-MAKING ALGORITHM BASED ON DEEP REINFORCEMENT LEARNING

1)THE DESIGN OF ACTION SPACE AND STATE SPACE

2)THE REWARD FUNCTION OF THE AIR COMBAT SITUATION

3)ALGORITHM PROCEDURE

IV.EXPERIMENT AND ANALYSIS

A.EXPERIMENTAL PARAMETER SETTINGS

1)PARAMETER SETTINGS OF TD3 ALGORITHM

2)PARAMETER SETTINGS OF MISSILE AND UAV

3)THE STRUCTURE OF POLICY NETWORK AND VALUE NETWORK

B.SIMULATION EXPERIMENT AND ANALYSIS

1)CONVERGENCE SPEED COMPARISON

2)TEST RESULTS COMPARISON

V.CONCLUSION

ACKNOWLEDGEMENTS

ETHICAL STATEMENT

CONFLICT OF INTERESTS

REFERENCES