JAIT

I.INTRODUCTION

With the development of the Internet and the popularization of smart devices, the collection and use of personal data, as well as data protection, are key research topics. To address this issue, privacy protection research has become increasingly important [1,2]. In the field of data privacy protection, federated learning is an emerging research direction that can effectively protect personal data privacy. Federated learning is on the grounds of the ideas of distributed computing and collaborative learning, allowing multiple participants to jointly train machine learning models without sharing raw data. Among them, federated average algorithm (FedAvg) is a commonly used federated learning algorithm that achieves global model training by exchanging model updates between local participants. The federal average algorithm has the advantage of protecting personal data privacy, but there is still a risk of privacy leakage in some sensitive tasks [3,4]. To further improve the protection level of personal data privacy, differential privacy has become a commonly used privacy protection technology. Differential privacy protects sensitive personal information by adding noise to the original data to alter the dataset [5,6]. In privacy data, data imbalance refers to a situation where the sample size varies greatly between different categories in a dataset. This situation is common in tasks involving privacy data, where some categories are sensitive or have less data volume compared to others, resulting in data imbalance. This shows that data imbalance has a more obvious effect on privacy protection. In situations where data is imbalanced and left unaddressed, individual data points may contain sensitive information, thereby increasing the risk of privacy violations if used or maliciously leaked. To address this issue, this study combines differential privacy with convolutional neural network (CNN) and proposes the Differentially Private CNNs with Adaptive Gradient Descent (DPAGD-CNN) algorithm. By combining the federal average algorithm and differential privacy CNNs, this study aims to use privacy protection models to promote the development of privacy protection technology. Then, it can provide effective solutions for personal data privacy protection in practical applications.

The respect of the paper is organized as follows. Section II presents the related studies. Section III deals with data imbalance on the grounds of the FedAvg. In Section III, based on data balancing processing, a privacy protection model is constructed by combining differential privacy with CNN. Section IV verifies the performance of the constructed model for comment classification through simulation experiments and practical applications. Section V is a discussion of the research results. Section VI summarizes the experimental results and analyzes the advantages and disadvantages of the research methods used.

II.RELATED WORK

With the rapid development of the Internet and big data technology, there are privacy breaches and security risks in the collection, storage, and use of data. How to protect the privacy and security of user data is an urgent problem that needs to be solved. Therefore, numerous experts and scholars have conducted in-depth research. Scholars such as Sun Z. have proposed a two-stage privacy protection mechanism on the grounds of blockchain to protect data privacy. This mechanism consisted of a dual perturbation local differential privacy algorithm and a blockchain, which perturbed location information through differential privacy and then utilized blockchain technology to ensure the integrity of data transmission. The results indicated that the protection mechanism can effectively protect the factors of staff and has a high service quality [7]. Zhang X. et al. proposed a distributed personalized tag anonymity algorithm to address personal privacy protection in social networks. The study divided and processed privacy information into three levels to achieve message transmission and node value updates, thereby increasing the protection factor. The results indicated that the algorithm can significantly reduce the risk of anonymity in social network datasets and increase the effectiveness of the data [8]. Tiwari D. et al. proposed a lightweight secure encryption algorithm to protect the privacy of data of Internet devices during transmission. This algorithm can use information permutation to generate pseudo-random sequences and generate new key streams during data transmission, thereby providing protection. The results indicated that the algorithm can effectively resist any existing data attacks [9]. To solve the privacy security of mobile crowdsourcing data, Wang W and other scholars proposed a mobile crowdsourcing federated learning system on the grounds of blockchain and edge computing. The system first utilized dual local perturbation local differential privacy to protect data privacy and location privacy and then merged the data through multimodal transformation. The results indicated that the system has strong adaptability and practical value on real datasets [10].

In the research of privacy protection, some experts and scholars have introduced mobile edge computing to optimize the process of data processing. The capabilities of mobile edge computing are utilized to significantly reduce data transmission latency, improve privacy protection, and help solve the problem of data imbalance. Wu W and other scholars designed a multi-layer joint learning protocol on the grounds of federated learning. This protocol aggregated edge-level and cloud-level data and then processed nodes using relaxation factors. The results showed that the system can significantly shorten the cycle length of joint learning, improve the global convergence speed by 12 times, and reduce energy consumption by 58% [11]. To deal with resource constraints and heterogeneity in edge computing, Wang Z. et al. designed an edge server collaboration system by combining deep neural networks with edge computing. The system first trained each device and offloaded some intermediate data output from hidden layers to appropriate edge servers for collaborative training. The results showed that the system can roughly increase the speed of edge computing by 2.3–4.9 times [12]. To improve the dynamic deployment capability of end users, Xu X. proposed a privacy-aware service deployment method using federated learning in cloud edge computing. This method transferred local service requests from edge servers to the cloud through model weight exchange and distributed training of aggregated data, avoiding the original data transmission. The results indicated that in the testing of the dataset, this method can significantly improve the data security of end users and enhance the overall service quality [13].

In summary, the privacy protection model constructed on the grounds of the FedAvg and differential privacy CNN is of great significance in the research of user personal privacy protection. This study aims to provide new research ideas for the field of personal privacy protection.

III.DESIGN OF PRIVACY PROTECTION MODEL ON THE GROUNDS OF FedAvg AND DIFFERENTIAL PRIVACY CNN

The design of privacy protection models on the grounds of FedAvg and differential privacy CNN can achieve good model performance and prediction accuracy while protecting individual data privacy.

A.DATA IMBALANCE PROCESSING ON THE GROUNDS OF FedAvg

Federated learning is a distributed machine learning method aimed at protecting the privacy and security of user data. In traditional centralized machine learning, user data needs to be uploaded to a central server for model training, which poses a risk of privacy leakage. In federated learning, data is kept on the local device, and model training is conducted on the local device, only uploading the updated results of the model [14–16]. It then performs collaborative training on all updated model results to obtain the global model. The process of optimizing data using federated learning can be represented by formula (1):

\min_{ω} \sum_{k = 1}^{m} p_{k} F_{k} (ω)

(1)

In formula (1), $ω$ represents the model parameters, $m$ represents the number of participants involved in the statistics, $F_{k}$ represents the local objective function of the participants in the statistics, and $p_{k}$ represents the weight values of different participants. Federated learning can be divided into horizontal federated learning, vertical federated learning, and transfer federated learning on the grounds of different types of learning. The three types of federated learning methods are illustrated in Fig. 1.

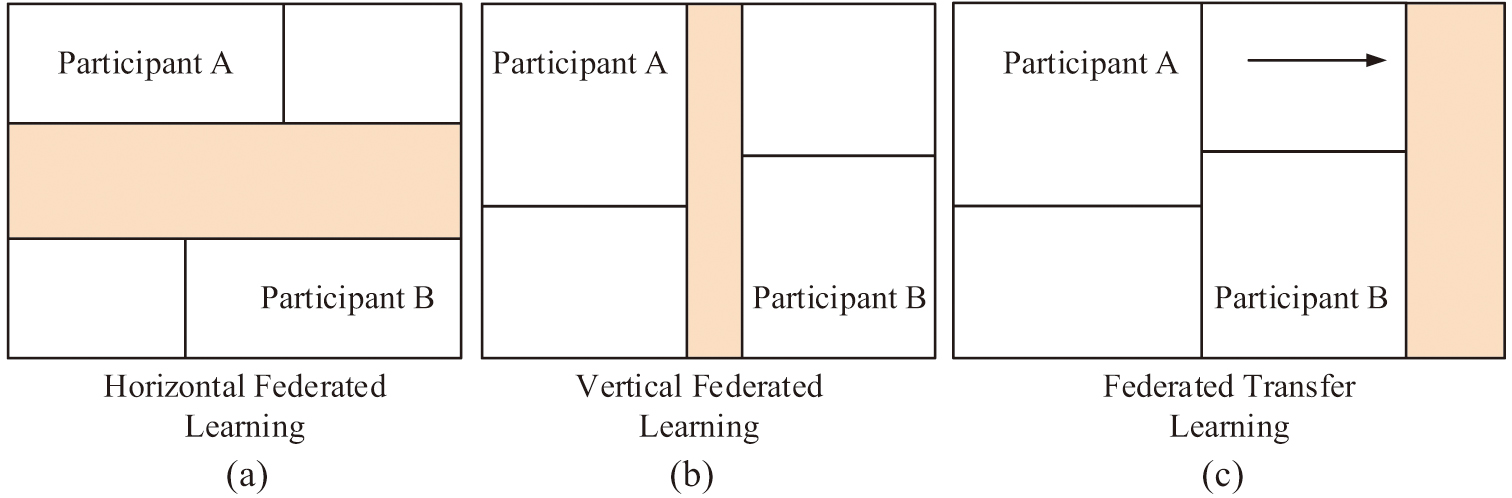Fig. 1. Three types of schematic diagrams of federated learning methods.

Figure 1(a) represents horizontal federated learning, in which different machine learning models average the parameters after local training to improve the overall model performance. Figure 1(b) represents vertical federation learning, in which participants have different feature spaces but share a portion of samples. Figure 1(c) illustrates federated migration learning, which is a combination of horizontal and vertical federation learning. It solves the problem of data samples and feature space not being exactly the same between participants, where the federation averaging algorithm belongs to horizontal federation learning. The study employs the federation averaging algorithm for model construction in horizontal federated learning. This allows different machine learning models to average their parameters after local training, resulting in an improved overall model performance. The study also found that data imbalance is prevalent in federal learning data processing, which may trigger information leakage, bias, discrimination, and unfair results. And it reduces the effectiveness of privacy protection through the study of related federal learning data processing. Therefore, measures need to be taken to address data imbalance to ensure privacy and fairness. The study uses the FedAvg algorithm to deal with data imbalance, which maintains data privacy, does not share sensitive data, adapts to local data features, and improves model generalization. The algorithm is based on the stochastic gradient descent algorithm improvement, which initializes the weights and distributes them to each device or computing node for training through a central server. This method optimizes model training to improve the efficiency and accuracy of data processing while also protecting privacy [17–19]. After each iteration, a certain proportion of participants will be selected from the iteration results for optimization. The optimization objective function at this point can be represented by formula (2):

f (u) = \frac{1}{n} \sum_{i = 1}^{n} f_{i} (ω)

(2)

In formula (2), $n$ represents the total number of participants in the sample and $f_{i} (ω)$ represents the loss value of the model parameters for predicting the $i$ -th data. According to $f_{i} (ω)$ , the loss prediction value of the $k$ -th participant can be calculated, which can be represented by formula (3):

F_{k} (ω) = \frac{1}{n_{k}} \sum_{i \in p_{k}}^{n} f_{i} (ω)

(3)

In formula (3), $F_{k} (ω)$ represents the predicted loss value of the $k$ th participant and $n_{k}$ represents the $k$ -th participant in the total sample size of the participants. At this point, the overall loss function of the federation can be represented by formula (4):

f (ω) = \sum_{k = 1}^{k} \frac{n_{k}}{n} F_{k} (ω)

(4)

After obtaining the overall loss function, it is necessary to use the gradient and learning rate of the $k$ -th participant in the total number of samples to solve for the parameters of different iteration rounds, which can be represented by formula (5):

ω_{t + 1}^{k} \leftarrow ω_{t}^{k} - η \nabla F_{k} (ω)

(5)

In formula (5), $ω_{t}^{k}$ represents the new parameter value of the $k$ -th participant after round $t$ , $ω_{t + 1}^{k}$ represents the new parameter value of the $k$ th participant after iteration $t + 1$ round, $η$ represents learning rate, and $\nabla F_{k} (ω)$ represents gradient. The above research demonstrates that the FedAvg algorithm obtains a new solution after completing each round of iterative training. For fixed participants, after completing each round of iterative training, a certain proportion of participants will be randomly selected for this round of iterative training. At this point, the corresponding central server can be represented by formula (6) for execution:

ω_{t + 1} \leftarrow ω_{t} - η \sum_{k = 1}^{K} \frac{n_{k}}{n} g_{k}

(6)

In formula (6), $K$ represents the total number of clients. The FedAvg algorithm performs local random gradient descent through the client and is combined with the server to improve the evaluation performance of the algorithm. Random gradient descent can be represented by formula (7):

ω_{t + 1} \leftarrow \sum_{k = 1}^{K} \frac{n_{k}}{n} ω_{t + 1}^{k}

(7)

Through the analysis of stochastic gradient descent, it was found that the FedAvg algorithm can perform load calculations on local participants. Then it undergoes multiple iterations of training to reduce the total number of training iterations for the global model, thereby reducing communication consumption throughout the entire process. The federal average algorithm can balance data distribution, alleviate data imbalance, and improve the generalization performance of the model by integrating model parameters from different participants. Through the collaboration between the participants and the central server, the FedAvg algorithm completed the entire federated learning process, balanced the imbalanced data, and distributed the balanced data to all participants. The specific process of FedAvg algorithm in handling data imbalance is shown in Fig. 2.

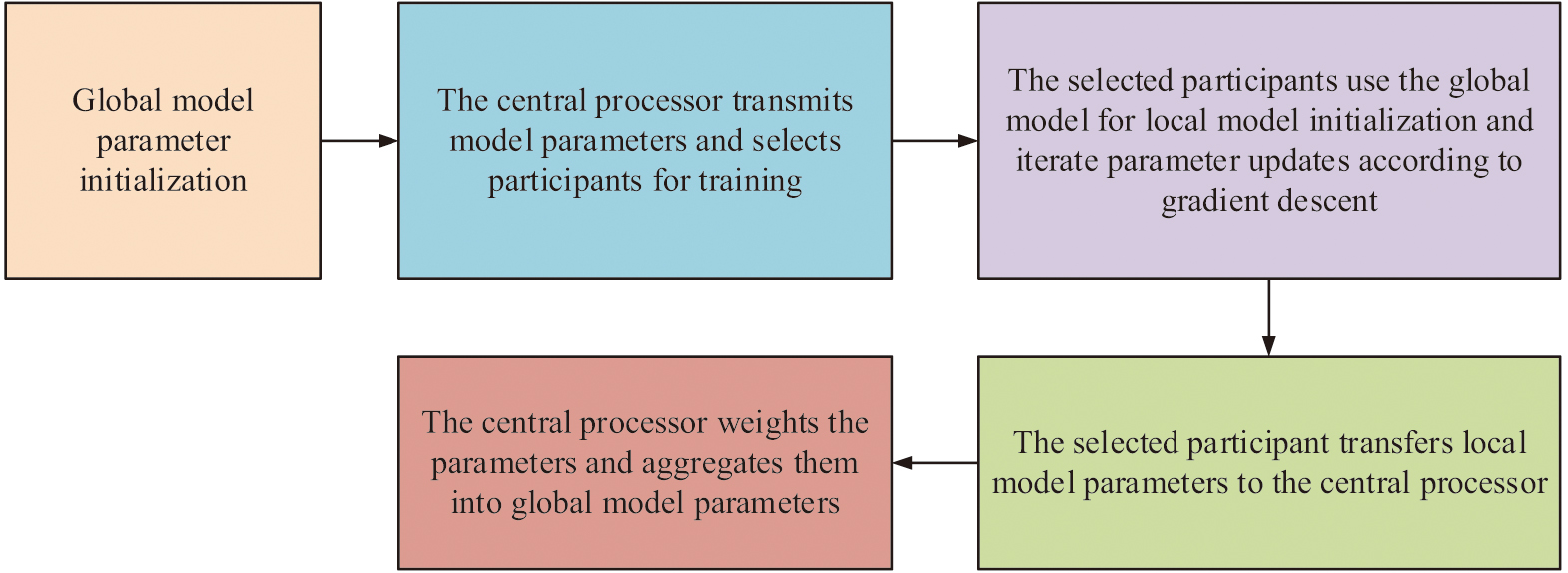Fig. 2. Flowchart of FedAvg algorithm for handling data imbalance.

On the grounds of Fig. 2, it is found that the FedAvg algorithm runs optimization algorithms such as random gradient descent on each device to update local model parameters. Then it uploads the updated model parameters to the server, which averages the model parameters of each device to obtain the globally optimal model parameters. Finally, it distributes the globally optimal model parameters to various devices.

B.CONSTRUCTION OF DPAGD-CNN PRIVACY PROTECTION MODEL ON THE GROUNDS OF FEDERATED LEARNING

After using the FedAvg algorithm to handle data imbalance, the data is balanced, and privacy protection research can be conducted using the data of each participating user. There is a risk of data theft during the upload process [5,20–21]. To reduce data risk and enhance attack resistance and privacy protection, the study combines CNN and differential privacy to construct a DPAGD-CNN model with adaptive gradient descent. The model uses adaptive gradient descent to iteratively optimize the parameters, ensuring data integrity and privacy protection. The loss function is set, the gradient is calculated, and the model is updated along the opposite direction. When solving the parameters will be performed in the DPAGD-CNN model, it is necessary to set the loss function that should be set, then calculate the gradient of the model using the training samples, and finally make the model change in the opposite direction of the descending gradient [22–24]. The setting of the learning rate is very important in this process. If the learning rate is too high, it will make it difficult for the model to converge in the later stage. If the learning rate is too low, it will lead to a decrease in the learning efficiency of the model and a longer training time. Therefore, the study needs to set the learning rate from the beginning, and the learning rate exponential decay strategy used in the study can be represented by formula (8):

η_{t + 1} = η_{t} \times d e c a y_r a t e, s . t . d e c a y_r a t e \in (0, 1)

(8)

In formula (8), $η_{t + 1}$ represents the set learning rate, $η_{t}$ represents the actual learning rate, and $d e c a y_r a t e$ represents the decay rate. The use of a learning rate decay strategy can ensure that the learning rate in the model can be adjusted in a timely manner, ensuring that the updating ability of the model can meet the requirements of data training. The relationship between learning rate decay and model update is shown in Fig. 3.

Fig. 3. Relationship between learning rate decay and model update.

In the DPAGD-CNN model, to ensure that the prediction accuracy is not affected during the gradient descent process, Gaussian distribution noise was added to the noise. The update of parameters is also achieved through gradient descent. Due to the differential privacy in the model, the gradient descent optimization can be represented by formula (9):

ω_{t + 1} = ω_{t} - η (\nabla f (ω_{t}) + N (0, σ^{2}))

(9)

In formula (9), $\nabla$ represents the gradient operator, $f (ω_{t})$ represents the loss function utilized in the optimization process, $N (0, σ^{2})$ represents the Gaussian distribution noise introduced on the gradient during the optimization, and $σ$ represents the noise variance. When using the DPAGD-CNN model for iterative operations, the number of iterations has an impact on privacy budget and noise variance. If the model has been iterated for M rounds, the privacy budget at this time can be represented by formula (10):

ϑ = ϑ_{1} + ϑ_{2} + \dots + ϑ_{M}

(10)

In formula (10), $ϑ$ represents the privacy budget. To ensure the high robustness and accuracy of the model, the privacy budget was set, and the Gaussian noise variance at this time can be represented by formula (11):

σ \geq \frac{Δ f}{ϑ} \sqrt{2 \ln (1.25 / δ)}

(11)

In formula (11), $Δ f$ represents global sensitivity and $δ$ represents the relaxation factor. Further simplification of formula (11) yields formula (12):

σ = \frac{Δ f}{ϑ}

(12)

According to formula (12), the magnitude of introducing Gaussian noise is directly proportional to global sensitivity and inversely proportional to privacy budget. Global sensitivity can be represented by formula (13):

Δ f = \max ‖ f (D_{1}) - f (D_{2}) ‖

(13)

In formula (13), $D_{1}$ and $D_{2}$ represent two adjacent user data information. After completing each iteration, the model will allocate a portion of $ϑ$ , and the allocated privacy budget is represented by $ϑ_{t}$ . Due to the model being an adaptive model, when allocating privacy budgets, different sizes of noise will be allocated during the gradient descent process according to the adaptive requirements. This is to meet the adaptive requirements of gradient descent and ensure that each iteration has an adaptive privacy budget. As shown in Fig. 4, it is a schematic diagram on the grounds of adaptive gradient descent.

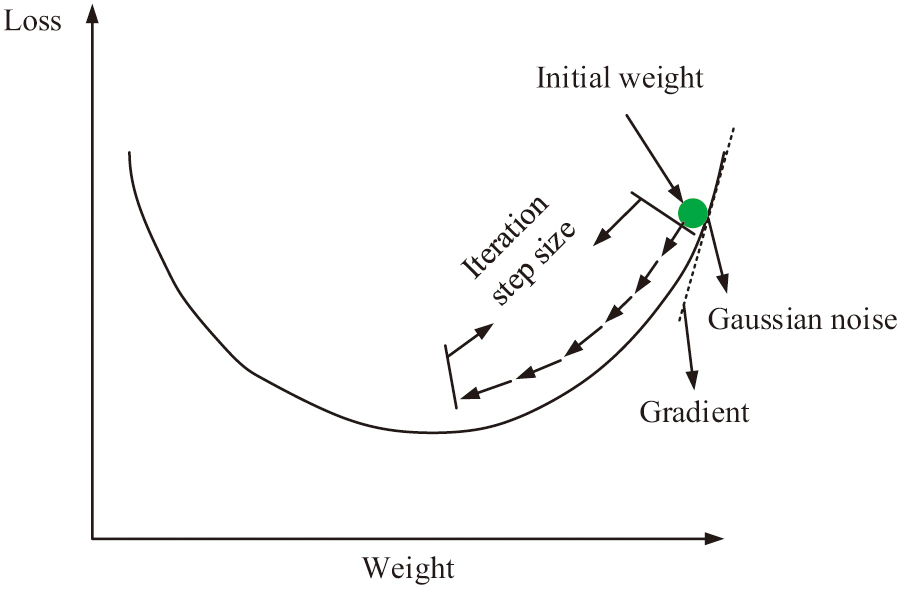Fig. 4. Schematic diagram of gradient descent on the grounds of adaptation.

After completing the adaptive gradient descent setting, the study analyzed a large number of literature and found that in federated learning, the larger the user data volume, the higher the robustness, and the lower the global sensitivity. For users with imbalanced data, it is necessary to set the privacy budget to be the same for each user to ensure the same level of privacy protection. For users with different amounts of data, namely those with imbalanced data, differential privacy needs to be processed according to actual situations. This indicates that the adaptive gradient descent utilized by the model has excellent performance and can be applied to adjust various parameters, thereby ensuring the effectiveness of the model. The flowchart of the privacy protection model on the grounds of DPAGD-CNN is shown in Fig. 5.

Fig. 5. Flowchart of privacy protection model on the grounds of DPAGD-CNN.

In conjunction with the above, it is investigated to utilize FedAvg algorithm for data equalization in case of data imbalance and to protect the privacy of user data by combining CNN and differential privacy techniques. By introducing CNN, the model is able to detect and prevent the tampering of data by malicious attacks and ensure the integrity of data. Meanwhile, combining the differential privacy technique ensures the privacy of the data during the training process by adding the noise of Gaussian distribution. In the construction of the model, the adaptive gradient descent method is used, which makes the model adapt to different data distributions and training requirements by adjusting parameters such as learning rate, privacy budget, and noise variance. And in federated learning, the difference in the amount of user data affects the robustness and global sensitivity of the model, so the privacy budget needs to be reasonably allocated to ensure the consistency of the privacy protection level of each user. This not only solves the two major problems of data imbalance and privacy protection but also ensures that the data is balanced to detect malicious attacks using CNN. This shows that the FedAvg algorithm can effectively deal with the problem of data imbalance and be used for privacy protection.

IV.PERFORMANCE ANALYSIS OF PRIVACY PROTECTION MODEL ON THE GROUNDS OF FEDERATED LEARNING

To verify the performance of the constructed factor protection model, this study applied the model to the privacy protection of Internet users. It uses MINIST, CIFAR, and Iris datasets as detection datasets to analyze the performance of the model.

A.PERFORMANCE ANALYSIS OF PRIVACY PROTECTION MODELS

To verify the specific performance of privacy protection models, the study compared the FedAvg algorithm and the Federated Optimization in Heterogeneous Networks (FedProx) [25] with the DPAGD-CNN model as comparative methods. MNIST, CIFAR-10, and Iris are also used as experimental datasets for performance comparison with existing models and methods, where the MNIST dataset contains 70,000 handwritten digital images in grayscale, out of which 60,000 are used as a training set and 10,000 as a test set. The CIFAR-10 dataset contains 10 classes of RGB color images, which are airplanes, cars, birds, deer, cats, dogs, frogs, horses, boats, and trucks. This dataset contains a total of 50,000 training images and 10,000 test images. Iris dataset is a classic dataset commonly used in the field of machine learning. The results of the three methods on the accuracy of local data for different devices under the effect of privacy budget and slack factor are shown in Fig. 6. The purpose of this experiment is to verify the correlation between balanced data and privacy-protected data in privacy preservation.

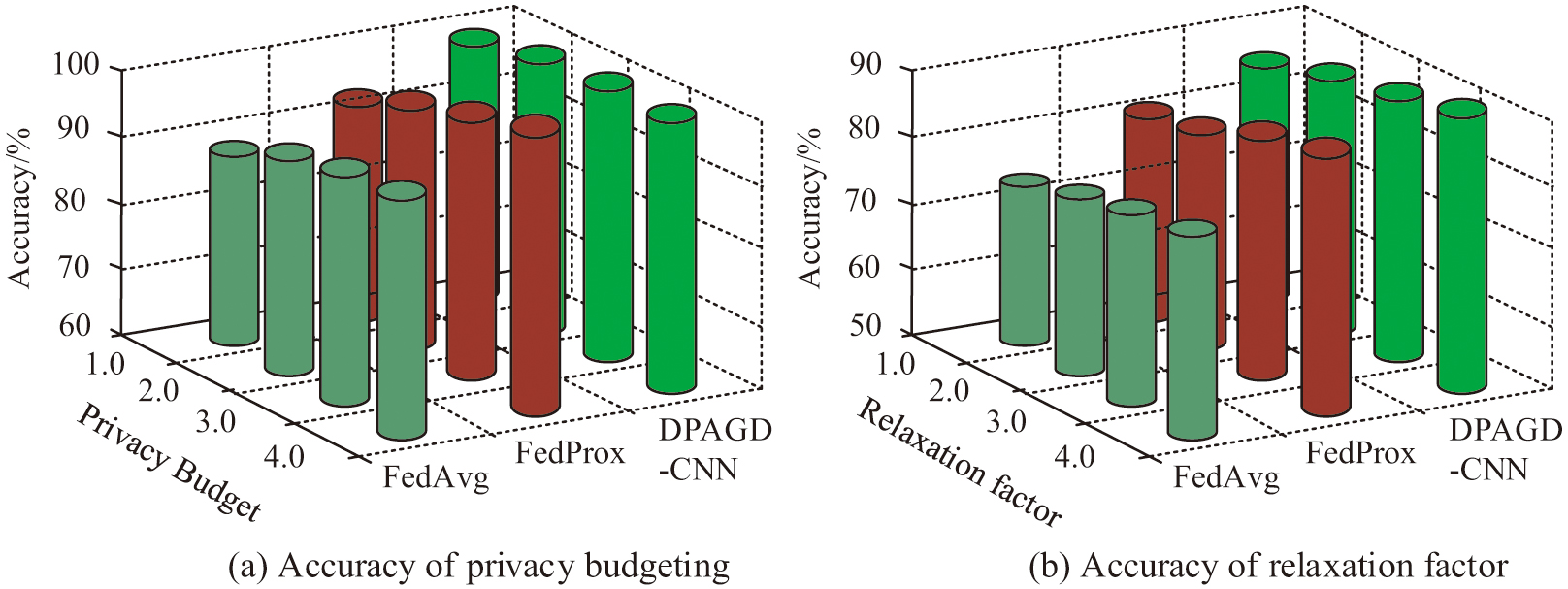Fig. 6. Comparison results of data recognition accuracy between different devices under the influence of privacy budget and relaxation factor.

As shown in Fig. 6(a), under the influence of privacy budget, as the privacy budget value increases, there are certain differences in the recognition accuracy results of the three methods for data, but the overall recognition accuracy is relatively high. The recognition accuracy of DPAGD-CNN is 97.27%, while the recognition accuracy of FedProx and FedAvg algorithms are 91.03% and 88.61%, respectively. Figure 6(b) shows that under the influence of the relaxation factor, there are also certain differences in the accuracy of data recognition among the three methods. The recognition accuracy of DPAGD-CNN is 93.15%, while the recognition accuracy of FedProx and FedAvg algorithms are 81.08% and 72.56%, respectively. This indicates that with the increase of privacy budget and relaxation factor, the recognition accuracy of data has improved to a certain extent, but it is necessary to control the range of set numbers. To verify the effectiveness of the model in handling data imbalance, the study also compared the three methods mentioned above. The comparison results of data recognition accuracy and data recall of the three methods in data imbalance are shown in Fig. 7. The purpose of this experiment is to evaluate the performance of the model in data imbalance in a more comprehensive manner.

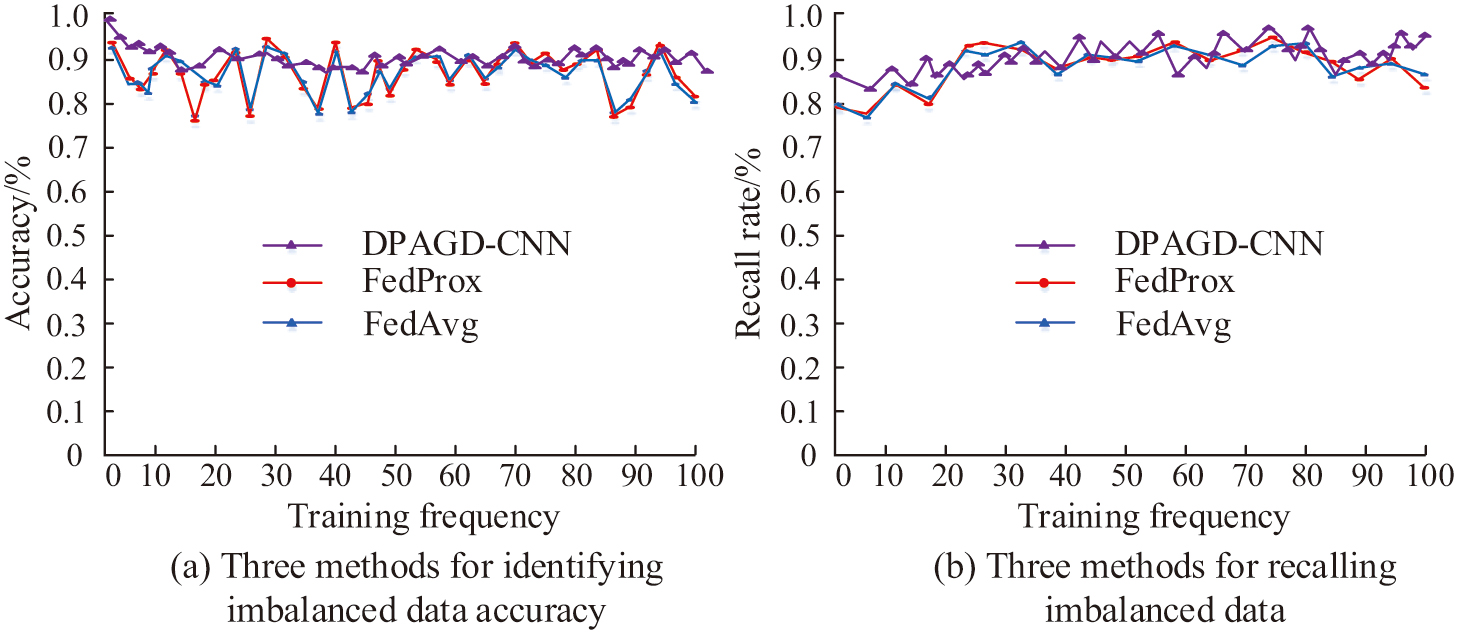Fig. 7. Comparison results of data recognition accuracy and data recall rate among three methods in data imbalance.

As shown in Fig. 7(a), in the case of imbalanced data, the data recognition accuracy of DPAGD-CNN, FedProx, and FedAvg algorithms are 92.11%, 88.36%, and 83.95%, respectively. As shown in Fig. 7(b), in the case of imbalanced data, the recall rates of DPAGD-CNN, FedProx, and FedAvg algorithms are 91.03%, 89.37%, and 86.75%, respectively. This indicates that the DPAGD-CNN model constructed in the study still has certain advantages in data processing ability in the case of imbalanced data, and the model has better robustness. To further verify the model’s ability in data processing, the study analyzed the data processing ability during the training process, using data classification accuracy and regression error as validation indicators. The results of the comparison of data classification accuracy and regression error of the three methods during the training process are shown in Fig. 8. The purpose of the experiment is to evaluate and optimize the performance of the models in the classification task and regression task.

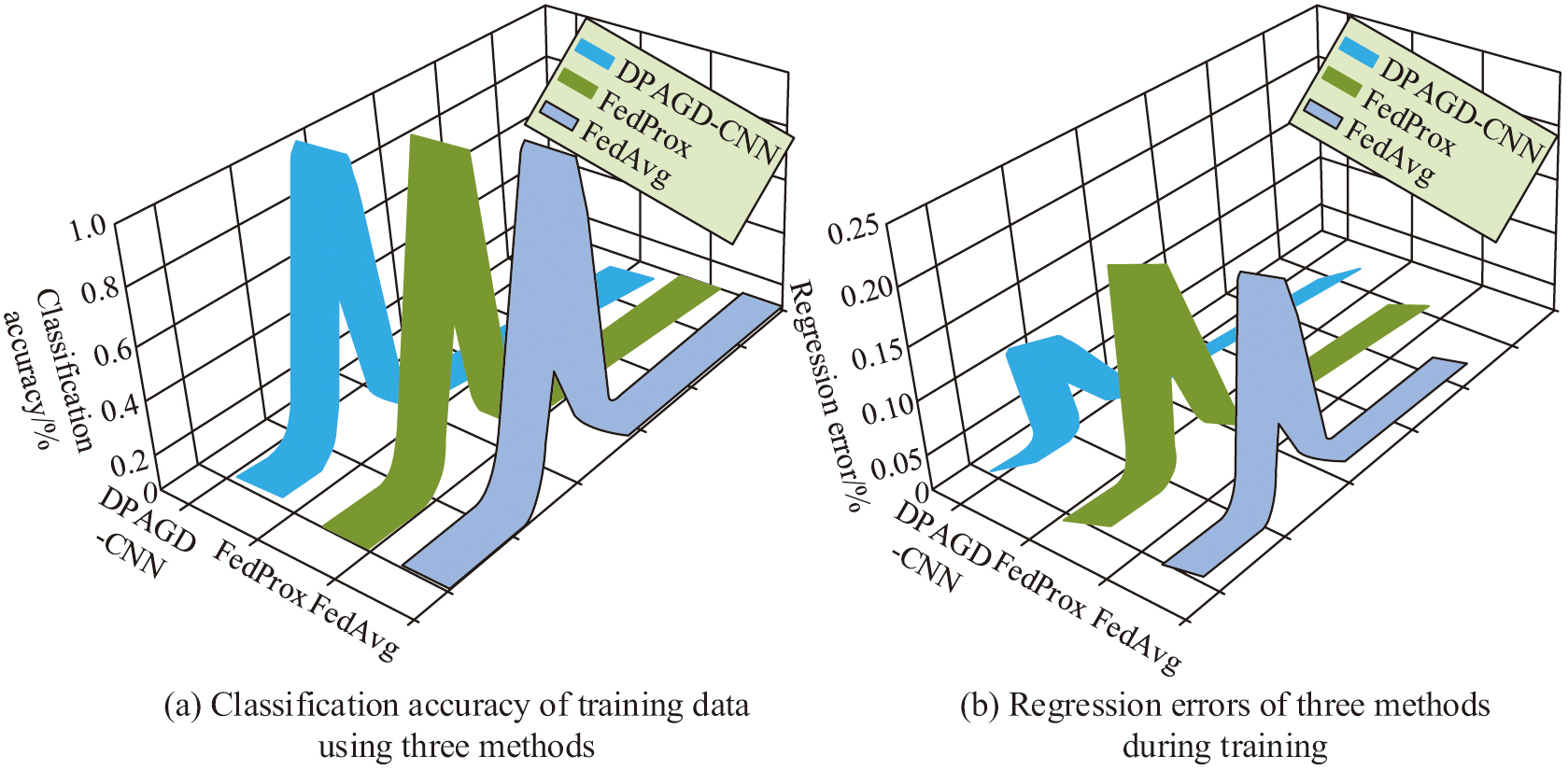Fig. 8. Comparison results of data classification accuracy and regression error among three methods during the training process.

As shown in Fig. 8(a), the higher the accuracy of data classification during the training process, the stronger the data processing ability of the method. The method with the highest classification accuracy in the figure is DPAGD-CNN, followed by FedProx algorithm and FedAvg algorithm. The data classification accuracy of the three is 95.31%, 90.66%, and 89.83%, respectively. As shown in Fig. 8(b), the smaller the regression error, the better the method can capture the relationship between data and predict future results more accurately. The regression errors of DPAGD-CNN, FedProx algorithm, and FedAvg algorithm are 9.03%, 13.87%, and 16.05%, respectively. This indicates that in the specific data training process, the DPAGD-CNN model constructed through research has stronger classification accuracy and the ability to capture the relationship between data, resulting in better results. To verify the performance of the DPAGD-CNN model in different data environments, different device data extraction ratios and local iteration times were used as validation indicators to evaluate the testing performance of the global model. The results of the comparison of data classification accuracy and regression error of the three methods during the training process are shown in Fig. 8. The purpose of the experiment is to evaluate and optimize the performance of the models in the classification task and regression task.

Figure 9(a) shows that different device extraction ratios have a certain impact on the testing accuracy of the model, and it does not mean that the higher the device extraction ratio, the higher the testing accuracy. When the extraction ratio is 60%, the testing accuracy is 92.18%. When the extraction ratio is 70%, the testing accuracy is 96.34%. When the extraction ratio is 80%, the testing accuracy is 90.74%. Figure 9(b) shows that when the local iteration number of the device is 30, as the number of experiments increases, it eventually tends to stabilize, with a testing accuracy of 95.28%. The testing accuracy for devices with 20 and 10 local iterations is 91.03% and 85.29%, respectively. This indicates that an adaptive data environment needs to be set up when testing the model to ensure ideal experimental results are obtained.

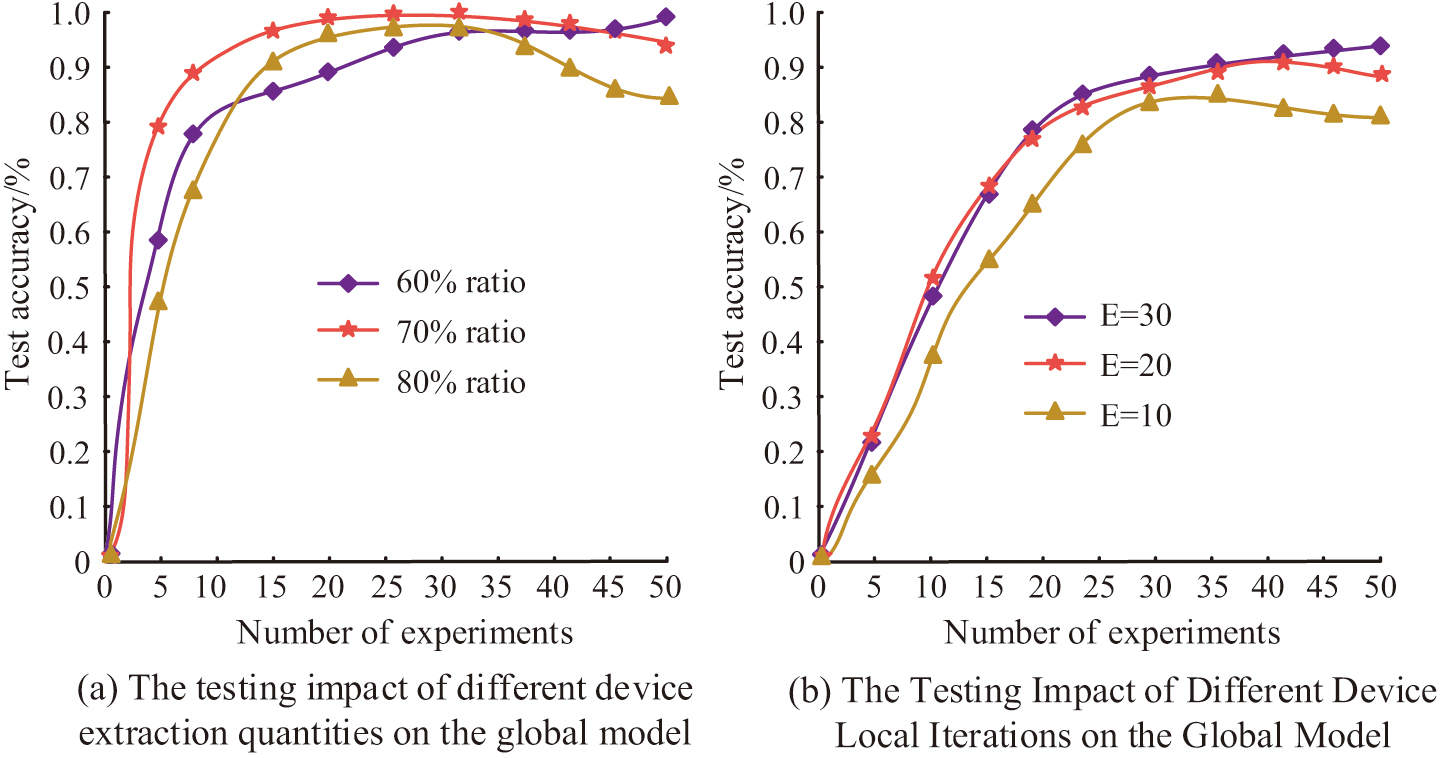Fig. 9. The impact of different extraction ratios and iteration times on model testing results.

B.APPLICATION PERFORMANCE ANALYSIS OF PRIVACY PROTECTION MODELS

To verify the specific application performance of the privacy protection model, this study takes MINIST, CIFAR, and Iris datasets as inputs and uses the model to process the information in the datasets to complete the performance verification. This study compares the impact of whether data balancing is performed on three datasets and whether a research construction model is used on the accuracy of data processing. The results of the accuracy comparison among the three datasets under different processing conditions are shown in Fig. 10. This experiment enables a better understanding of the performance of the dataset and optimization model through the comparison of accuracy rates.

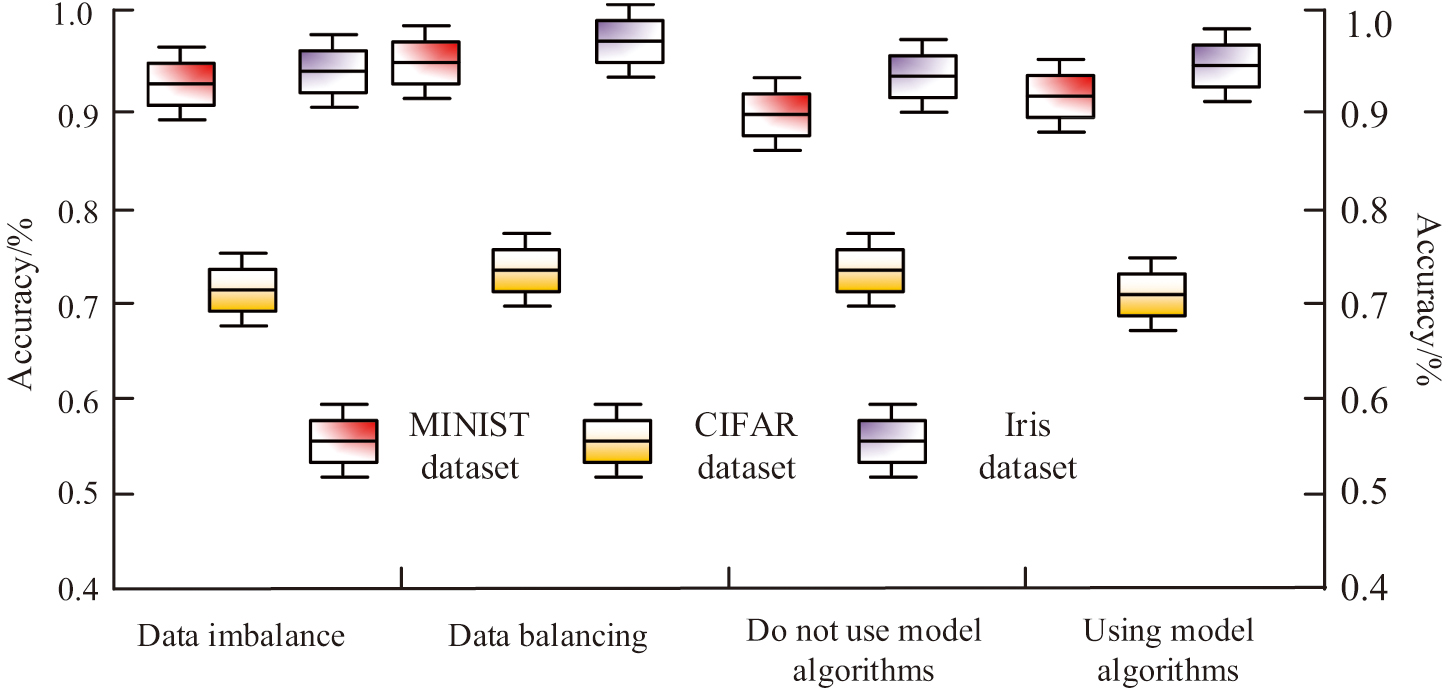Fig. 10. Comparison of accuracy results among three datasets under different processing conditions.

Figure 10 shows that the accuracy rates for imbalanced data in the MINIST, CIFAR, and Iris datasets are 93.27%, 75.81%, and 93.94%, respectively. The accuracy rates during data balancing are 94.86%, 76.03%, and 95.07%, respectively. Under the use of model algorithms, the accuracy rates in the three datasets were 94.27%, 73.88%, and 94.85%, respectively. The accuracy without using the model algorithm was 91.62%, 73.01%, and 91.89%, respectively. This indicates that the performance after data balancing and referencing the model is significantly better than the unused performance, which also reflects the superiority of building the model. To verify the performance of the model in application, the study compares it with traditional methods and true values, using the time consumption and data utilization rate of each communication as comparison indicators. The comparison result of the time consumption and data utilization of each communication is shown in Fig. 11. The purpose of this experiment is to verify the specific performance of the model through the time consumed and the utilization rate and to be able to use this as a basis to enhance the system performance and improve the user experience.

Fig. 11. Comparison results of time consumption and data utilization for each communication.

Figure 11(a) shows that there is a significant difference in the time consumption of the three methods for completing each communication. The true value for completing each communication is 1.86s, the model method takes 2.15s, and the traditional method takes 2.89s. According to Fig. 11(b), the data utilization rate of the true values is 95.49%, the data utilization rate of the model method is 88.76%, and the data utilization rate of the traditional method is 79.81%. This indicates that the gap between the model and the true value is significantly reduced compared to the gap between traditional methods and the true value. This indicates that the model method can improve the performance of privacy protection process, reduce communication time, and also reduce the risk of data theft. To further verify the role and effectiveness of the model in privacy protection of hidden data, the study takes the efficiency of privacy data protection and the number of information leaks as detection indicators. The results of privacy protection efficiency and information leakage comparison in the privacy protection process are shown in Fig. 12. The purpose of the experiment is to verify the privacy protection ability of the model and promote the development of information security.

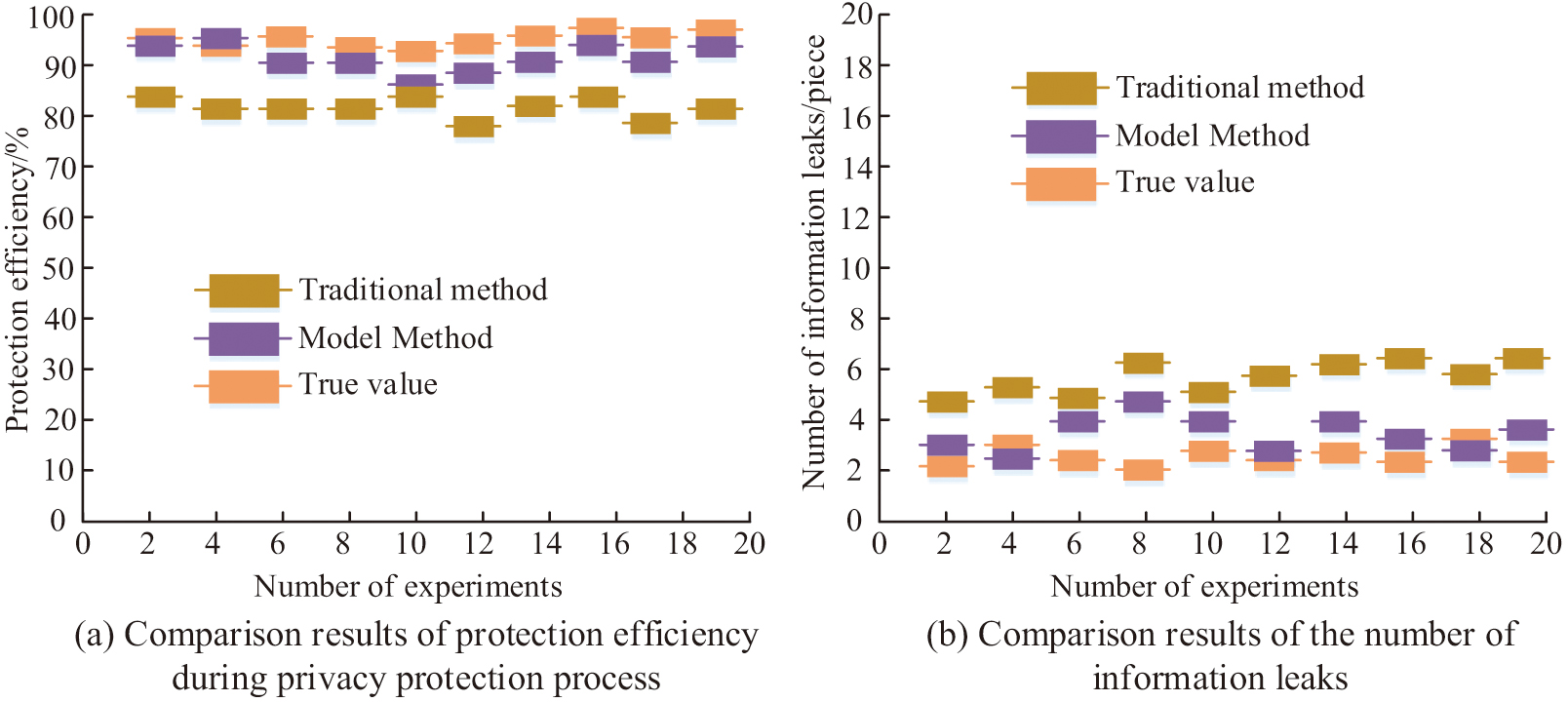Fig. 12. Comparison of privacy protection efficiency and information leakage during the privacy protection process.

Figure 12(a) shows that in the privacy protection process, the efficiency of real protection is 99.84%, the protection efficiency of model methods is 94.89%, and the protection efficiency of traditional methods is 87.51%. Figure 12(b) shows that during the privacy protection process, the true number of information leaks is 3, the model method has 5.1 information leaks, and the traditional method has 6.2 information leaks. The difference between the model method and the actual value is minimal, and there is a significant improvement compared to traditional methods. This indicates that the model has strong universality in practical applications and has the ability to improve data privacy protection. In order to further validate the application performance of the model, the study combines the two methods of security aggregation and multi-party security combined with differential privacy to validate the performance of the model constructed by the study, as shown in Fig. 13, which shows the results of the comparison of the reliability of the three methods in privacy protection.

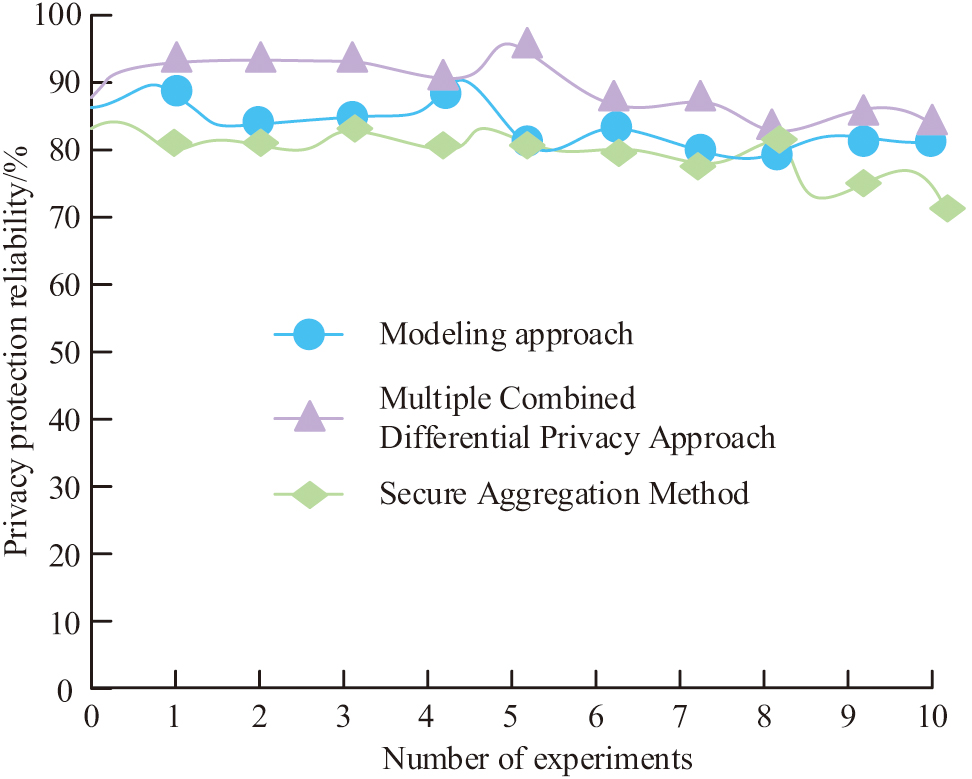Fig. 13. Reliability comparison results of three methods in privacy protection.

From the comparative analysis shown in Fig. 13, it can be seen that the reliability of the privacy protection model constructed in the study falls between the security aggregation method and the multi-party combined differential privacy method throughout the entire protection process. The study shows that the privacy model has a reliability of 90.08%. The multi-party combined differential privacy method has a privacy protection reliability of 95.62%, while the secure aggregation method has a privacy protection reliability of 85.87%. This indicates that the privacy protection model constructed in the study currently has high reliability and credibility in this field. The study reveals that the model’s performance varies when different datasets are used for validation. This is due to differences in characteristics, distribution, and quality among the datasets. The variation in results can be attributed to differences in the datasets, including variations in their characteristics, distribution, and quality. These differences can impact the model’s performance. The composite algorithm may exhibit bias during data preprocessing and model training. Therefore, it is important to combine the data characteristics and algorithm advantages to develop a suitable strategy for optimizing model performance for different datasets.

V.DISCUSSION

Through the above research, although privacy protection research based on FedAvg with differential privacy CNNs has brought important breakthroughs in the field of data privacy protection, there are still some limitations and weaknesses. First, from the perspective of communication cost, federated learning requires frequent data exchanges between each participant and the central server. In the case of a large number of devices or large model parameters, such communication may lead to a huge data transmission burden, which in turn increases the communication cost and time delay. Second, system heterogeneity is another issue that cannot be ignored. Since different devices or computing nodes may have different hardware configurations, data distributions, and training environments, this may lead to inconsistency and instability in model training. Although the FedAvg algorithm is able to handle this heterogeneity to some extent, its effectiveness may still be affected by the differences between devices. In addition, parameter selection for differential privacy is a challenging issue. The setting of the privacy budget requires a trade-off between privacy protection and data availability. If the privacy budget is set too high, it may not provide sufficient privacy protection. Conversely, if it is set too low, it may seriously compromise data availability, which in turn affects the training effect and performance of the model. Finally, the complexity and robustness of CNNs are also factors to be considered. CNNs, as a deep learning model, have a complex structure and a large number of parameters, which may lead to high computational costs for model training. Meanwhile, the sensitivity of CNN to noise and outliers may be further exacerbated in the context of differential privacy, which may affect the stability and performance of the model.

In summary, the privacy-preserving research based on the federal average algorithm with differential privacy CNNs faces certain limitations and weaknesses in terms of communication cost, system heterogeneity, parameter selection for differential privacy, and complexity and robustness of CNNs. In the future, these limitations and weaknesses can be taken as research directions and worked on to solve these problems to further improve the privacy-preserving effect and model performance.

VI.CONCLUSION

With the rise of the Internet and big data, personal privacy is facing increasing threats. Subsequently, there is a demand for personal privacy protection technology. To effectively protect privacy, a privacy protection model was constructed by combining FedAvg and differential privacy CNN. The results showed that in the MINIST, CIFAR, and Iris datasets, the accuracy of data balancing was 94.86%, 76.03%, and 95.07%, respectively. The accuracy of data processing under the use of the model was 94.27%, 73.88%, and 94.85%, respectively. The model took 2.15 seconds only to complete one communication, with a protection efficiency of 94.83%. All comparison items were superior to the comparison method. This indicated that the model could effectively protect the privacy and security of user data, while improving the accuracy and generalization performance of the model. Compared with other related studies, the model proposed in this study could better address complex practical problems while protecting user privacy, and it had important application value and practical significance. However, there were still shortcomings in the research. The federal average algorithm was used in the data processing process, and there has not been much research on other federal algorithms. The next step is to study other federal algorithms for data processing to obtain better research results.

Privacy Protection Based on Federated Learning