JAIT

I.INTRODUCTION

With the rapid development of new energy vehicles, the demand for power batteries is increasing day by day. All solid batteries are becoming more widely used in automotive power due to their longer service life and higher safety [1]. However, compared with liquid electrolytes, the conductivity of solid electrolyte materials is usually lower, which hinders its more application in power batteries [2]. With the development of machine learning, in order to improve the conductive performance of solid-state batteries, many researchers utilize machine learning models to find conductive materials with higher properties from the material library. In order to improve the efficiency of material screening, reduce the cost and cycle of material screening, Qi Xingyi et al. reviewed and summarized the different functions of big data technology and artificial intelligence technology on different types of new materials in the research and application of machine learning algorithms on new materials. In particular, they highlighted the role of machine learning algorithms in discovering new materials in material databases and in predicting and optimizing material properties [3]. Chen Xiang et al. reviewed and summarized the application of machine learning in ionic conductivity prediction of solid-state electrolyte materials from the aspects of multi-scale simulation, ionic conductivity prediction and auxiliary battery experimental research. They believed that the active learning algorithm represented by the random forest model could achieve the optimal optimization of ionic conductivity on the existing 30% datasets and had great potential in the screening of solid electrolyte materials [4].

In terms of the electrochemical properties of solid-state battery electrolyte materials, aluminum-air batteries have extremely high crustal resource reserves and relatively suitable electrochemical properties, and they have a wide range of application prospects. However, compared with electrode materials, there is relatively less research on aluminum air electrolytes. In view of this phenomenon, Zhu Kui et al. studied and summarized the classic aluminum-air solid-state electrolyte materials, which laid a foundation for the optimization of electrolyte materials for aluminum-air batteries [5]. Pu Jiansu et al. combined classification algorithms, projection algorithms, and clustering algorithms, constructed a visual analysis system for the screening of solid-state electrolyte materials and conductivity prediction. Moreover, they reconstructed the results of ionic conductivity prediction of various machine learning models, which verified the effectiveness of machine learning models in the prediction of solid electrolyte materials meeting specific performance requirements [6]. Based on the above research, this paper combines machine learning algorithms with solid electrolyte material screening. On the one hand, methods such as exhaustive method, FSHD feature selection method and Pearson coefficient are used to achieve dimensionality reduction screening of feature combinations. On the one hand, methods such as enumeration method, FSHD feature selection method and Pearson coefficient are used to achieve dimension reduction screening of feature combinations. On the other hand, logistic regression model and random forest model are trained by using the selected subset of optimal features, and the trained optimal model is applied to predict the conductivity of all solid-state electrolyte materials in the common battery material library, so as to improve the analysis and prediction performance of machine learning model on high-dimensional small data samples.

The organizational structure of the remaining parts of this article is as follows: Section II reviews the literature on machine learning and screening of high-performance solid electrolyte materials, and proposes a small sample based feature screening and prediction method for solid electrolyte materials to address the current problems of small prediction model data and difficulty in selecting the optimal feature subset; Section III introduces machine learning algorithm used in this study; Section IV selects feature dimension reduction and screening methods under high-dimensional small data, and designs the model construction based on the selected optimal feature set; Section V evaluates the performance of feature screening method and machine model by experimental method, thus verifying the effectiveness of the proposed prediction method; Section VI summarizes contents and research values of this article, and provides prospects for future research based on the existing problems in the study.

II.RELATED Work

At present, it is generally believed that low ionic conductivity is difficult to compete with traditional organic liquid electrolytes in the screening of solid-state electrolyte materials for batteries, so it has become a trend to find potential high-performance solid-state electrolyte materials. At present, solid electrolytes can be classified into oxides, sulfides, halides, polymers, and composite solid electrolytes according to the difference of their components, and high ionic conductivity is an important indicator of high-performance solid electrolytes. The development of computer technology has provided the design of new materials with a more effective exploration of the phase and component space of materials. In particular, the combination of machine learning based on data driving, deep learning and theoretical computing has become a hot spot in material screening and physicochemical property prediction. By relying on algorithms, general laws or experiences can be learned from a large amount of data and applied to unknown data, and then prediction or screening can be realized, which has become the “quaternary scientific paradigm” of material design. By using machine learning algorithms in the screening study of electrolyte materials, Meredig B et al. used machine learning models to predict the thermodynamic stability of any composition, so as to search 4,500 undiscovered new materials that may be stable ternary compounds from 1.6 million ternary compounds.

Olivynyk and Mar used SVM and RF to predict the crystal chemical structure of compounds. The contribution of these authors is to help experimenters break free from conventional thinking and discover unexpected new materials. Sendek et al. proposed a method to screen suitable solid-state electrolyte materials and constructed a data-driven ionic conductivity classification model through artificial intelligence and machine learning. To implement the model, it took two years to collect all known scientific data related to lithium-containing solid compounds, and used logistic regression algorithms to predict which materials were likely to exhibit high ionic conductivity. This prediction model used several confidence indicators to identify suitable candidate materials, including stability, cost, rich content, and lithium-ion conductivity. Finally, 21 kinds of promising candidate materials for solid electrolyte were selected from 12831 kinds of lithium crystals. However, the authors also said that the small number of training samples could affect the accuracy of structure-based prediction results to a certain extent, and the limitations of the results could be improved with the increase of sample size.

Kajita S et al. applied ensemble learning based on small data sets to the prediction of oxygen ion conductivity of solid oxide fuel cells. Combining descriptors, ridge regression, convolutional neural networks, and partial least squares were used for ensemble prediction screening, demonstrating a good prediction accuracy. Xiang Yan et al. applied Backward Propagation Neural Network (BPNN) to the ionic conductivity prediction of molten salts in the NdF₃-LiF-Nd₂O₃ system. Based on the three descriptors of temperature, LiF concentration and Nd₂O₃ concentration, a good prediction accuracy was finally achieved, and the prediction value and experimental error were about 3%.

The above research provides reference for the screening of solid-state electrolyte materials, but the model training usually requires a large number of sample data to predict the accuracy of results. Moreover, in practical applications, most ionic conductor screening or prediction models still have problems such as small data, difficulty in selecting optimal feature subset, and the prediction effect of existing methods is not stable. The solution of these problems can further promote the application and development of machine learning in the field of materials. Especially in the field of materials and other related scientific research, it is of great significance to develop high-dimensional small-sample machine learning and high-dimensional small-sample feature selection methods. Therefore, this paper adopted typical logistic regression algorithm and random forest algorithm for small sample analysis to analyze solid electrolyte materials, and combines the optimal feature subset selection method to achieve accurate prediction in the case of small data.

III.BASIC METHODS

A.LOGISTIC REGRESSION ALGORITHM

Logistic Regression (LR) is a linear regression model normalized by Sigmoid function [7]. It can also be regarded as a powerful explainable classification algorithm whose essence is linear regression. It is a relatively classical machine learning algorithm at present. Based on linear regression, the algorithm realizes the prediction of sample classes by adding a layer of Sigmoid function mapping between the result mapping and the feature. The function mapping result is a real value located in the (0,1) interval. When it is less than or equal to 0.5, its predicted class label is output as “0”, otherwise its predicted class label is output as “1”. The sigmoid function can be expressed as follows:

S i g m o i d (z) = \frac{1}{1 + e^{- z}}

(1)

Suppose the dimension of all features is $n$ , take the linear combination of sample features $(x_{1}, x_{2}, …, x_{n})$ as the independent variable, and calculate the linear regression result. According to the regression value obtained, it is then mapped to a probability value of an interval (0,1) through Sigmoid function as the final prediction result of the model. If the parameter of the linear layer is $θ$ , the calculation formulas for mapping process of the logistic regression algorithm are:

θ^{T} x = \sum_{i = 1}^{n} θ_{i} x_{i} = θ_{0} + θ_{1} x_{1} +, …, + θ_{n} x_{n}

(2)

h_{θ} (x) = S i g m o i d (θ^{T} x) + \frac{1}{1 + e^{- θ^{T} x}}

(3)

In the formula, $θ \in R^{N}$ , which is adaptively adjusted through training; $h_{θ} (x)$ is the predicted value output by the model, $h_{θ} (x) \in R$ .

Compared with other machine learning algorithms, interpretability of logistic regression algorithm lies not only in reflecting the interaction between things, but also in revealing and capturing the causal relationship between features and targets, so as to achieve faster and more accurate search for solid-state electrolyte materials with high ionic conductivity. It is a classification algorithm with strong adaptability to small datasets, relatively simple operation, and can provide interpretable feature coefficients. Therefore, this article chooses logistic regression algorithm to construct material prediction classification model.

B.RANDOM FOREST REGRESSION ALGORITHM

1.ALGORITHM PRINCIPLE

Random forest (RF) is an ensemble classifier containing multiple decision trees. It was first proposed by Breiman et al. as a classification and regression algorithm that utilizes multiple trees to train and predict samples [8]. Compared with neural network algorithm and single decision tree algorithm, RF regression algorithm requires less computation resources, has higher prediction accuracy, and has better anti-overfitting and robustness when dealing with regression problems. RF regression algorithm is a prediction model framework composed of a set of decision trees, which integrates multiple decision trees and makes collective decisions through voting, so as to obtain the final regression prediction result. A set of rules is treated as a decision tree, and a random set of input variables is selected and replaced with a regression tree from the original data set. Set the segmentation point with minimum squared error as $s$ and the segmentation variable as $j$ , segment each tree according to the standards of $s$ and $j$ . The segmentation process can be calculated as:

\min_{j, s} [\min_{c_{1}} \sum_{R_{1}} {(y_{i} - c_{1})}^{2} + \min_{c_{2}} \sum_{R_{2}} {(y_{i} - c_{2})}^{2}]

(4)

Where $R_{1}$ and $R_{2}$ represent the two regions defined by classification point $s$ and split variable $j$ , and $y$ is the output variable of the data set. $R_{1}$ and $R_{2}$ are defined as follows:

R_{1} (j, s) = {x | x^{(j)} \leq s}

(5)

R_{2} (j, s) = {x | x^{(j)} > s}

(6)

Following the above process, the segmentation is repeated until the regression decision tree does not continue to grow. In this case, the solution of the decision tree model is:

f (x) = \sum_{i = 1}^{n} (\frac{1}{N_{i}} \sum_{\in R_{i} (j, s)} y_{k}) I (x \in R_{i})

(7)

In the formula, $I (x \in R_{i})$ is the index function, when $x \in R_{i}$ , $I (x \in R_{i}) = 1$ , otherwise $I (x \in R_{i}) = 0$ .

Finally, the average predicted value of each decision tree can be obtained, then the final predicted value of the random forest regression model is obtained. The above steps can be illustrated in Fig. 1.

2.PARAMETER OPTIMIZATION

In previous research, researchers often optimized the parameters of random forest regression models by drawing learning curves or using grid search methods. This improves the prediction effect of the random forest regression model to a certain extent, but because of the fixed number of optimization steps, the optimization speed and precision are always difficult to reach the ideal. Therefore, in order to obtain the optimal parameters without affecting the efficiency of the model, this paper uses the adaptive genetic algorithm in literature [9] as the parameter optimization method of the model.

Adaptive Genetic Algorithm (AGA) is an improved genetic algorithm that utilizes the idea of biological genetic evolution. Traditional genetic algorithms update populations through genetic operations such as crossover and mutation to produce new dominant individuals. Because of the constant updating probability, it is easy to discard the dominant particles with greater fitness, resulting in unstable algorithm results and easy to fall into local optimization. Adaptive genetic algorithm assigns different crossover and mutation probabilities to particles based on their fitness level. In the updating process, individuals with higher fitness have a higher probability of crossover operation and a lower probability of mutation operation. The probability of crossover and mutation in individuals with lower fitness is reversed. With this adaptive adjustment, particles with high fitting in the particles are more likely to be retained, and it is easier to generate new particles during the update process, thereby reducing the probability of falling into the local optimum. The fitness value of the particle is expressed as $f'$ , and the particle crossover and mutation probabilities $P_{c}$ and $P_{m}$ in the adaptive genetic algorithm are calculated as follows:

P_{c} = {\begin{matrix} P_{c 1} - \frac{(P_{c 1} - P_{c 2}) (\bar{f} - f')}{(f_{\max} - \bar{f})} & f' \leq \bar{f} \\ P_{c 1} f' > \bar{f} \end{matrix}

(8)

P_{m} = {\begin{matrix} \frac{P_{m 1} (f_{\max} - f)}{(f_{\max} - \bar{f})} & f \geq \bar{f} \\ P_{m 2} f < \bar{f} \end{matrix}

(9)

Where, $\bar{f}$ and $f_{\max}$ are the average fitness value and the maximum fitness value. $P_{c 1}$ and $P_{c 2}$ represent the upper and lower limits of the crossover probabilities, whose values are 0.5 and 1, respectively. $P_{m 1}$ and $P_{m 2}$ are the upper and lower limits of the mutation probabilities, whose values are 0.001 and 0.001 respectively.

Adaptive genetic algorithm is utilized to optimize the parameters of random forest framework and decision tree of random forest regression model. By utilizing the superior global optimization ability of genetic algorithms and the dynamic updating of genetic operations through adaptive methods, the optimal parameters of the model can be found more quickly, thereby achieving the maximization of model prediction performance. The parameter optimization process of random forest regression model based on adaptive genetic algorithm can be represented as follows:

IV.CONSTRUCTION OF IONIC CONDUCTIVITY PREDICTION MODEL

Feature descriptors are a set of representative descriptive features of materials that are related to target attributes [10]. Machine learning models characterize materials based on feature descriptors, so as to predict and obtain materials that contain the desired properties [11]. In this paper, we first construct a data set containing room temperature copper ionic conductivity and simple descriptors. The descriptors are combined by enumeration method. Enumeration method, also known as exhaustive method, is an algorithm that relies on traversing all elements to solve problems in the simplest and most direct way, and it is often used to solve small-scale problems. Compared with other algorithms, enumeration method can list all states and combinations completely, ensuring the correctness of results. In this paper, dimension reduction is carried out for the small-sample data prediction problem, so before predicting the features, enumeration method is used to combine the feature descriptors, which improves the accuracy of the results and lays the foundation for subsequent prediction without causing large time overhead. Then, based on the combination of all features, feature selection method based on high-dimensional small data (FSHD) proposed by Yan Jiaxi in the article “Design and Application of Solid State Electrolyte Material Screening and Conductivity Prediction Software Based on Machine Learning” is used to achieve dimension reduction screening of feature combinations. The method trains the machine learning model by feature subset and quickly screens feature subset selection method of potential ionic conductors in the database by evaluating the performance of the model. The accuracy for the screening task of small data sets is significantly improved compared with the classical screening methods such as Wrapper and Embedding. A set of feature combinations corresponding to the model with the best evaluation performance is the optimal feature combination. As the mapping experience from the input feature to the target attribute, users can quickly search the corresponding label of the target attribute in the material library according to the input feature. Finally, a logistic regression model and a random forest regression model are constructed based on the mapping experience, and conductivity prediction is completed on the test set. It should be noted that it is necessary to avoid the problem that the similarity between the corresponding sub-datasets of the optimal feature combination obtained by screening is too high, which will affect the generalization of the construction model. Before constructing the prediction model, Pearson correlation coefficient is introduced to retest the cross-correlation between feature combination variables [12,13].

Pearson correlation coefficient, also known as Pearson product-moment correlation coefficient, is a commonly used data clustering method that utilizes covariance to calculate the correlation between two random variables [14]. It compares the correlation between two variables based on their covariance size. If the two variables are also greater than their expected values, the covariance value between the two variables is positive, which means that the two variables have the same trend of change, that is, there is a strong correlation between them. If one of the two variables is greater than its expected value, but the other is less than its expected value, it means that the two variables show an opposite trend, and the covariance between the two variables is negative, indicating that the correlation between the two is weak or none. Assuming that any two variables in the subset are $x_{i}$ and $y_{i}$ , then Pearson correlation coefficient is calculated as follows:

r = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sqrt{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2} \sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}}}

(10)

In the formula, $\bar{x}$ and $\bar{y}$ are the mean values in $n$ th experiments.

The conductivity prediction process of solid electrolyte materials based on logistic regression algorithm and random forest regression algorithm is shown in Fig. 2 [15].

According to the feature descriptors contained in the data set, exhaustive enumeration is performed on all feature combinations, and a logistic regression model is constructed based on the data set under the feature combination. Let the number of all features be $n$ and the number of models to be evaluated is $2^{n} - 1$ . This paper selects the model with the highest AUC value of the ROC curve as the optimal logistic regression model, and selects its corresponding feature combination and data subset as the selected optimal feature combination and subset [16]. Then, the random forest regression model is constructed based on the selected optimal feature combination, and the ionic conductivity of the materials is predicted by utilizing random forest regression model [17].

V.EVALUATION MODEL

A.EXPERIMENTAL ENVIRONMENT

This experiment is based on PyQt5 software and Python3.6.5 programming language to build a conductivity prediction system for solid electrolyte materials, which is mainly divided into three main parts: feature search, feature selection, model construction and evaluation [18]. The system is equipped with an Intel(R) Core(TM) i7-13700K CPU and an NVIDIA GeForce RTX 3050 graphics card with 8GB of video memory.

B.EXPERIMENTAL PARAMETERS

The parameter quality of machine learning model affects model training effect. Among them, the number of decision trees directly affects fitting results of the model. In order to find the most suitable number of decision trees for the dataset in this article and avoid overfitting or low accuracy during model training, prediction results of models with 50, 100, 500, 600, and 700 decision trees were compared, and root mean square error was used to characterize the prediction accuracy of models [19]. The results show that with the increase of the number of decision trees, the prediction accuracy of models is also increasing. When the number of decision trees is 600, the prediction error value of the model is the smallest, which is 0.137. When the number of decision trees increases to 700, the memory occupied by the model and the training increase, but the prediction accuracy does not increase significantly, so the number of decision trees of the model is set to 600. In the case of single factor variable test, step sizes are set to 0.001, 0.005, 0.01, 0.015, 0.020, respectively; The maximum depth of the tree is 5:15:5, 4:18:3, 3:20:2, 2:20:3; The minimum sample sizes of leaves are 0.01:0.07:0.7, 0.05:0.1:1, 0.1:0.5:5, 0.15: 0.75:7.5; The minimum values that restricted the further division of leaf trees are 0.05:0.75, 0.1:1.2, 0.15:1.5, 0.2:2.6; The number of classifiers is 50:200:150, 100:500:400, 150:550:300, 200:600:400. Other parameters of the model are adjusted by the same method, and the final training step of the model is set to 0.01, and the maximum depth of the decision tree is 3:20:2, and the minimum sample number of leaf nodes and the minimum value of the restriction subtree further partition are 0.1:0.5:5 and 0.1:1.2, respectively. The specified number of classifiers in random forest is 100:500:400.

C.EXPERIMENTAL DATA

The data for this experiment came from an open-source material project (MP) database jointly launched by Massachusetts Institute of Technology, the Lawrence Laboratory of the University of California, Berkeley and other authoritative institutions in 2011. This database contains approximately 125000 inorganic compound materials, their structures, properties, and other related information, and it provides multiple material screening methods to explore the changes in the quality inspection performance attributes of different materials [20]. In this paper, compounds with aluminum and their corresponding atomic structure information are searched from MP database, and the relatively high structural stability, metal stability, electronic conductivity and oxidative decomposition stability are selected as the screening conditions to select the optimal solid electrolyte materials related to aluminum-air batteries, thereby constituting the experimental data set [21]. According to the ratio of 8:2, it is divided into training set and test set, and the materials in the training set are labeled based on the judgment criterion that the ion conductivity value is greater than $1 \times 10^{- 4} S c m^{- 1}$ . Finally, a total of 18 features with strong correlation with ions are selected in the experiment, and those whose ionic conductivity value are greater than $1 \times 10^{- 4} S c m^{- 1}$ are labeled as “1”, which are regarded as positive samples with good ionic conductivity. In addition, features with ionic conductivity values less than or equal to $1 \times 10^{- 4} S c m^{- 1}$ are label as “0”, which are regarded as negative samples with poor ionic conductivity [22]. Table I shows all the features and descriptions in the training and test sets. All eigenvalues are normalized before use.

Table I. Selected Features and Their Descriptions

Feature	Description
AAV	Average atomic volume
VPA	mean anionic volume
SDLI	Standard deviation of Li-X ionic bond
LBI	Mean particle properties of Li-X bond
SDLC	Standard deviation of the mean adjacency number of Li atom
SNC	Sub-lattice average adjacency number
LLB	Average value of Li-Li bond
SBI	Average ionic properties of X-Y ionic bonds of sublattice
AFC	Anionic framework coordination
RNC	Ratio of LNC to SNC
LLSD	Average minimum separation distance of anion-anion
LASD	Average minimum separation distance of Li-anion
SPF	Packing fraction of sublattice
PF	Packing fraction of lattice
SLPE	Average straight-line path electronegativity
SLPW	Average straight-line path width

D.EVALUATION METHOD

In order to evaluate the generalization performance of the classification model and avoid the overfitting of the model in the training process, this paper uses the cross-validation method as the evaluation method to evaluate the accuracy of the model. Due to the small size of the data set in this paper, the classification model is constructed by exhaustively enumerating all feature combinations, and the different feature combinations are evaluated by the receiver operating characteristic curve (ROC), area under curve (AUC) of the ROC curve, and accuracy (Acc) of LOOCV (leave one out cross validation) [23]. ROC curve and AUC value are the main evaluation indicators for evaluating classification models, especially binary classification models. In particular, compared with the traditional evaluation indicators commonly used by classification models, namely accuracy, regression rate or F1 value, the AUC value focuses more on the scores of positive and negative samples rather than the specific scores, which is more suitable for evaluating the effect of ranking problems. In this paper, the goal of classification prediction is to find electrolyte materials with high ionic conductivity characteristics, rather than electrolyte materials with ionic conductivity characteristics. The stronger the ranking ability of the model, the higher the materials with high ionic conductivity in the results, and the easier to achieve the purpose of material screening. Therefore, this paper selects the feature combination with larger evaluation indicators as the optimal feature combination to form a training subset, and uses the tenfold cross validation method to comprehensively evaluate the classification accuracy of the model composed of the training subset. The calculation formula for the accuracy of the classification model is as follows:

A c c u r a c y = \frac{T P + T N}{T P + F N + F P + F N}

(11)

where, TP represents the number of samples whose predicted and true values are both positive, and TN represents the number of samples whose predicted and true values are both negative. FN represents the number of samples with positive predicted values and negative true values, and FP represents the number of samples with negative predicted values and positive true values. We draw the ROC curve using the true positive rate of the classification model in LOOCV process as the vertical axis and the false positive rate as the horizontal axis. We evaluate the performance of the classification model by AUC of ROC curve. The closer is the AUC value to 1, the more accurately can the classification model rank the samples with positive true values first, that is, the model has better classification performance.

For regression model, common evaluation indexes such as mean absolute error (MAE), mean square error (MSE) and determination coefficient are used for performance evaluation [24]. Among them, the mean absolute error represents the average value of the absolute error between the predicted value and the actual value, which is mainly used to reflect the accuracy of model classification and the actual situation of the predicted value error [25]. The mean square error represents the Euclidean distance between the predicted value and the actual value, and it is often used to measure the degree of deviation between the predicted value and the actual value, so as to evaluate the fitting effect of classification prediction models [26]. In this paper, the mean absolute error and mean square error are used as the evaluation indicators of the regression model. The calculation formulas of the two indicators are as follows:

M A E = \frac{1}{N} \sum_{i}^{N} | y_{i} - {\hat{y}}_{i} |

(12)

M S E = \frac{1}{N} {\sum_{i}^{N} (y_{i} - {\hat{y}}_{i})}^{2}

(13)

where, N is the total number of classified samples;

y_{i}

and

{\hat{y}}_{i}

represent the true value and predicted value of the sample respectively.

VI.EXPERIMENTAL RESULTS AND VERIFICATION

A.FEATURE SELECTION

In this paper, the enumeration method is adopted to list 18 feature descriptors to form feature combinations, and the combinations that contain the same number of feature descriptors are classified as one class for statistical analysis. The data distribution under different number of feature combinations is shown in Fig. 3 [27]. In order to reduce the subsequent computation quantity of logistic regression model, the combinations of the number of features of 1 and the number of features of 18 are eliminated. Therefore, there are 16 feature combinations obtained.

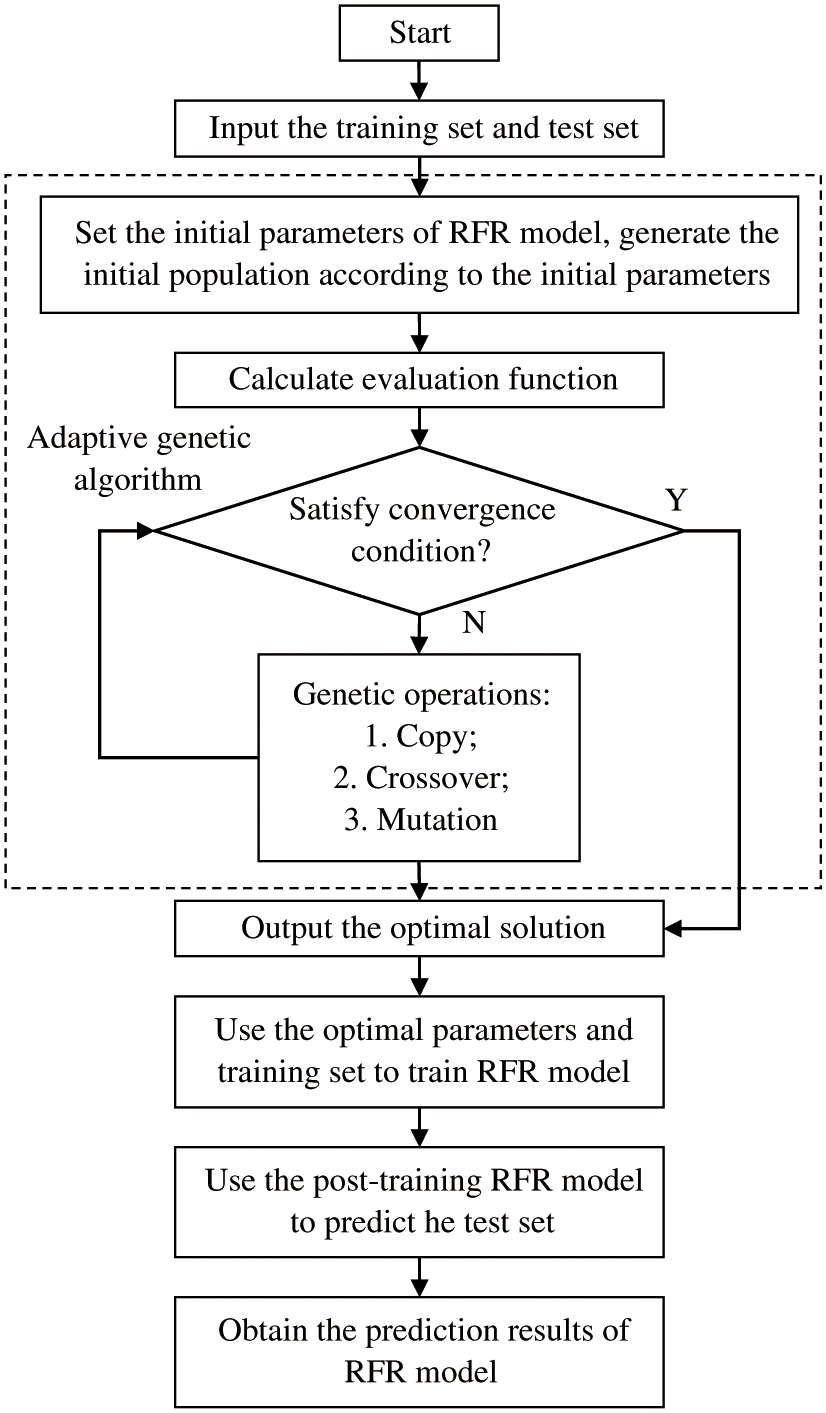Fig. 1. Random forest regression algorithm improved based on adaptive genetic algorithm.

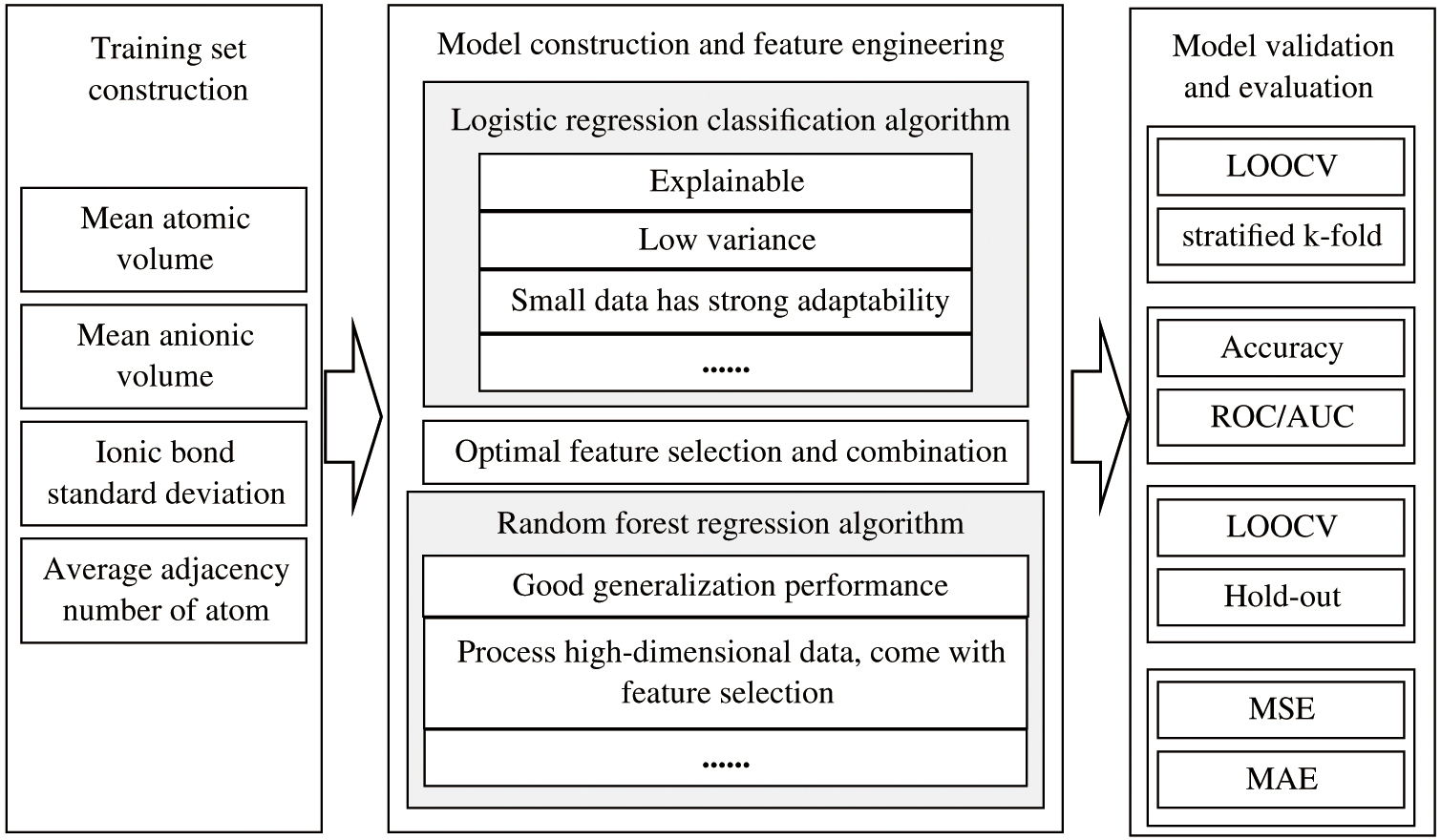Fig. 2. Conductivity prediction method of solid electrolyte materials based on machine learning model.

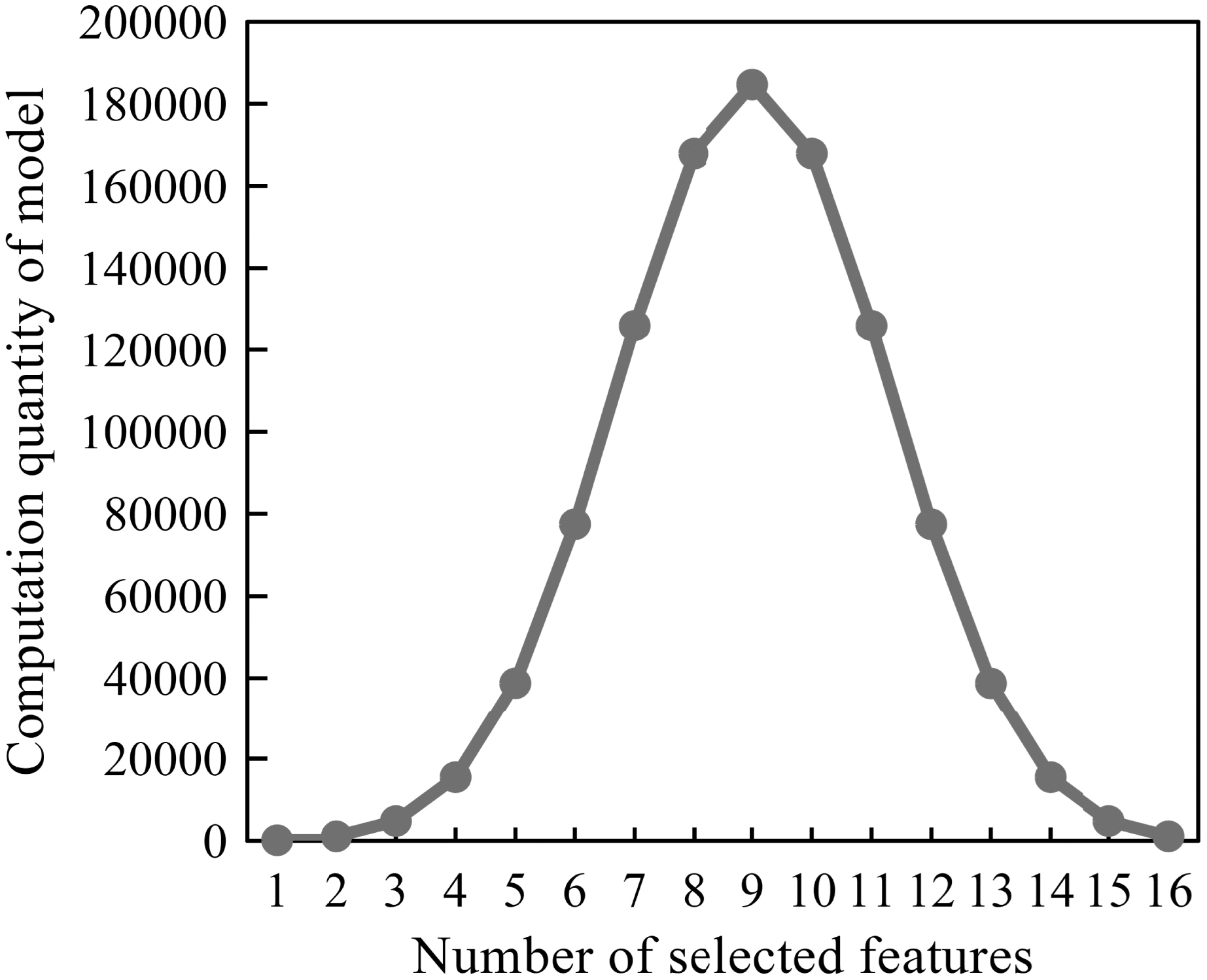Fig. 3. Distribution of different number of feature combinations.

The feature selection method based on high dimensional small data (FSHD) is used to realize the dimension reduction and screening of feature combination. Firstly, it exhaustively enumerates all feature combinations composed of two types of features, and then it uses the sub-datasets under these combinations to construct the model. Then, the maximum AUC value, the true positive rate (TPR) and false positive rate (FPR) are adopted [28]. Finally, this paper evaluates the performance of each subset corresponding to the feature combinations containing the two features and selects the optimal combination. On the basis of the selected combination, the remaining features are added in turn until all remaining features are traversed. The final feature combination is the optimal feature combination [29]. The results of the maximum AUC value of the subset under different number of feature combinations are shown in Fig. 4(a), and the feature combination with the best performance under each number is used as the representative evaluation result of the number of feature combinations:

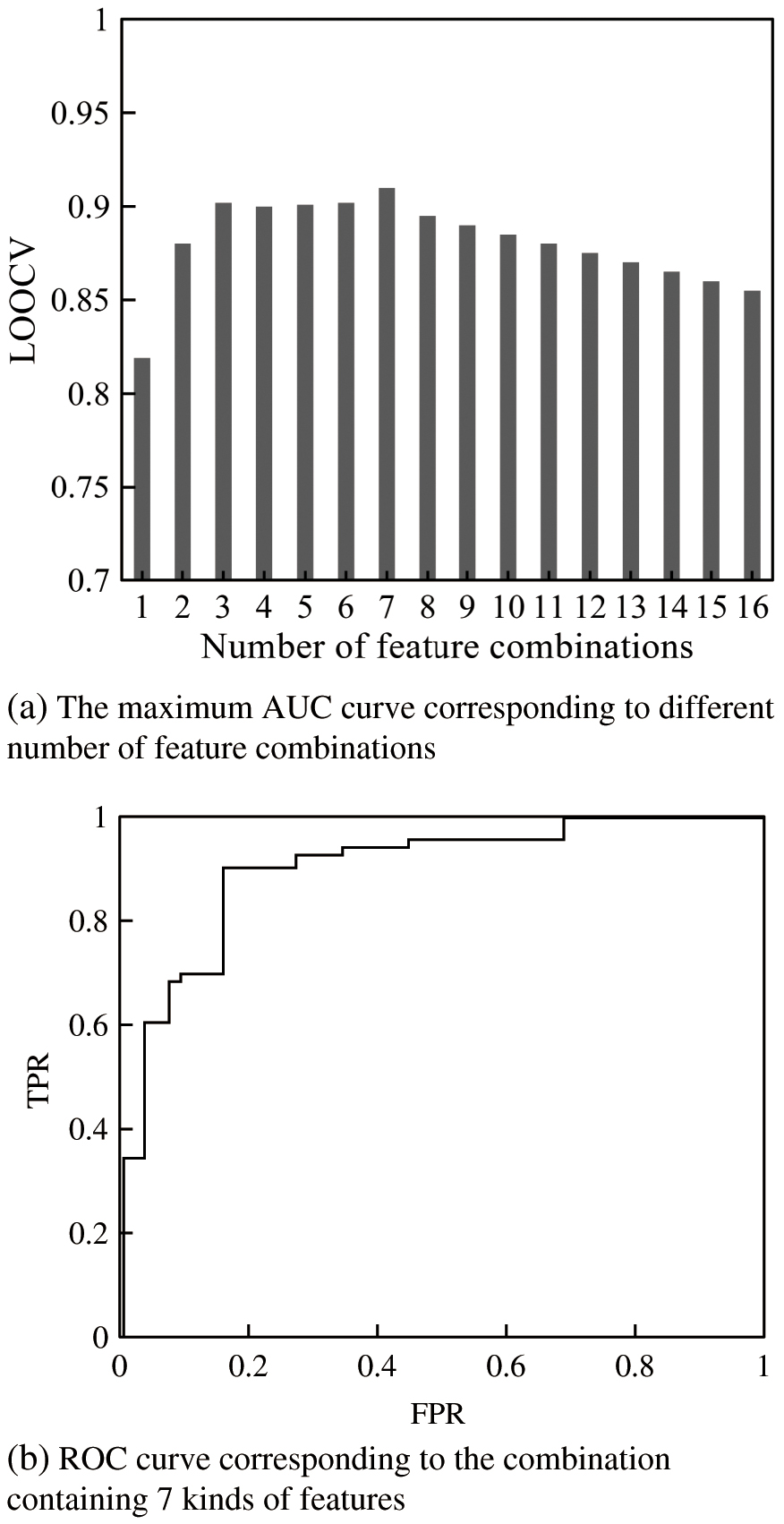Fig. 4. Comprehensive evaluation results of features. (a) The maximum AUC curve corresponding to different number of feature combinations. (b) ROC curve corresponding to the combination containing 7 kinds of features.

As shown in Fig. 4(a), the maximum AUC value of the model under the leave one out cross validation presents a trend of first rising and then decreasing with the increase of the number of feature combinations, and reaches the highest point of 0.92 when the number of feature combinations is 7. Furthermore, ROC curve of the combination composed of 7 features is calculated, and the results are shown in Fig. 3(b). As the purpose of this research is to identify materials with higher ionic conductivity, it can be seen from Fig. 4(b) that when the number of features is 7, the ROC curve of the constructed model is biased towards the upper left, indicating that the model will place positive samples at a higher position during the classification process, thus meeting the research purpose.

Verifying the effectiveness of FSHD feature selection method, this paper adopts common feature selection methods such as embedded embedded selection method and ES exhaustive model-based search method to screen the feature combinations on the data set [30]. Moreover, the corresponding AUC values and accuracy of the optimal feature combinations in LOOCV are compared with the evaluation results of the 7 kinds of feature combinations selected. The comparison results are shown in Table II. As can be seen, the AUC value and accuracy of the FSHD feature selection method are 0.907 and 0.868, respectively, which are much higher than the AUC value and accuracy of the combinations screened by the embedded embedded selection method. Although its accuracy is slightly lower than the accuracy of the ES exhaustive model-based search method, the detection speed is faster. On the whole, the method used has the best effect.

Table II. Performance Comparison of Different Feature Selection Methods

Feature selection method	Accuracy	AUC value
embedded	0.852	0.864
FSHD	0.868	0.907
ES	0.871	0.913

The degree of similarity between feature combinations can also have a certain impact on the performance and universality of classification models. The higher the degree of similarity, the more limited the description of the entire electrolyte properties by the constructed model, and the more difficult it is to screen out new materials that meet the requirements of high ionic conductivity in the material library. Therefore, in order to verify the accuracy of the above feature selection and ensure the generality performance of the constructed mode, Pearson correlation coefficient is used to evaluate the correlation between various features in the optimal feature combination [31,32]. The Pearson correlation coefficient between the 7 kinds of feature descriptors is shown in Fig. 5:

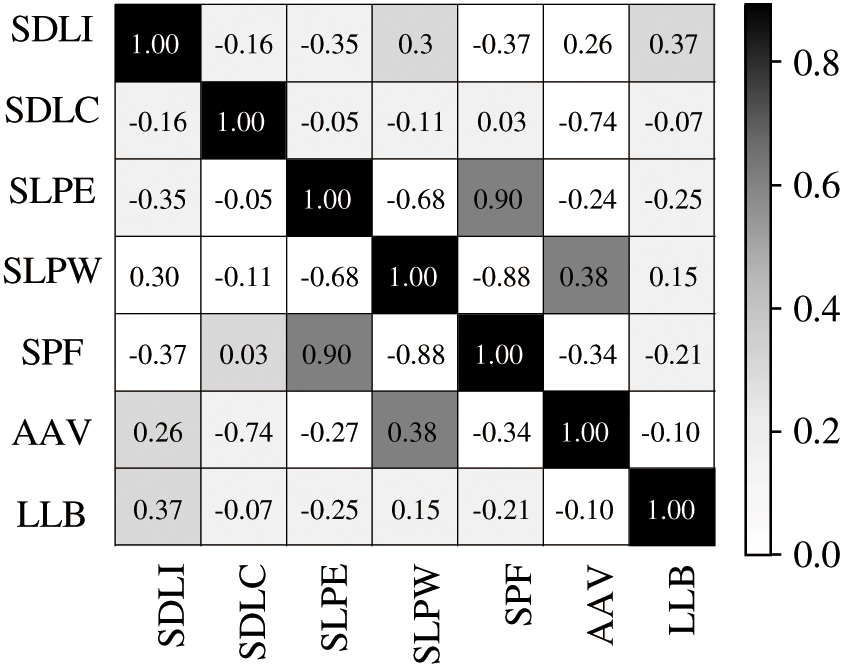Fig. 5. Pearson correlation coefficients of corresponding features in the optimal subset.

As shown in Fig. 5, the correlation coefficients of the seven kinds of feature variables selected are all lower than 0.4, which has weak correlation. This proves that the optimal feature subset obtained by the screening method using the LOOCV method has high quality, the correlation between the features in the subset is weak, and the description of the correlation between the material and the target is more comprehensive. Moreover, the random forest regression model constructed based on this feature combination also has strong generalization ability. It can still accurately and quickly find solid electrolyte materials related to aluminum air batteries with high ion conductivity in large-scale material libraries.

Therefore, seven features in the combination are selected as the optimal subset, and the features in the combination include SDLI, SDLC, SLPE, SLPW, SPF, AAV and LLB [33,34].

B.VERIFICATION OF PREDICTION RESULTS

1.VERIFICATION OF LR PREDICTION RESULTS

The regression model is constructed based on different numbers of feature combinations, and the performance of the selected feature combinations is tested by evaluating the performance of the model. The accuracy of logistic regression models with different feature combinations is shown in Fig. 5. The same combination is regarded as a kind of combination, and the highest accuracy is selected as the comprehensive accuracy of the combination with the same number of features. The comprehensive evaluation results of the logistic regression model are as follows:

As shown in Fig. 6, when the selected feature combination containing 7 features is used, the results of the training classification accuracy, the LOOCV accuracy and the ten-fold cross-validation accuracy of the model are 87.46%, 87.46% and 86.48%, respectively, indicating that the model has the highest classification accuracy. This proves the effectiveness of the feature screening method used, and the selected 7 features have an important impact on improving the ionic conductivity.

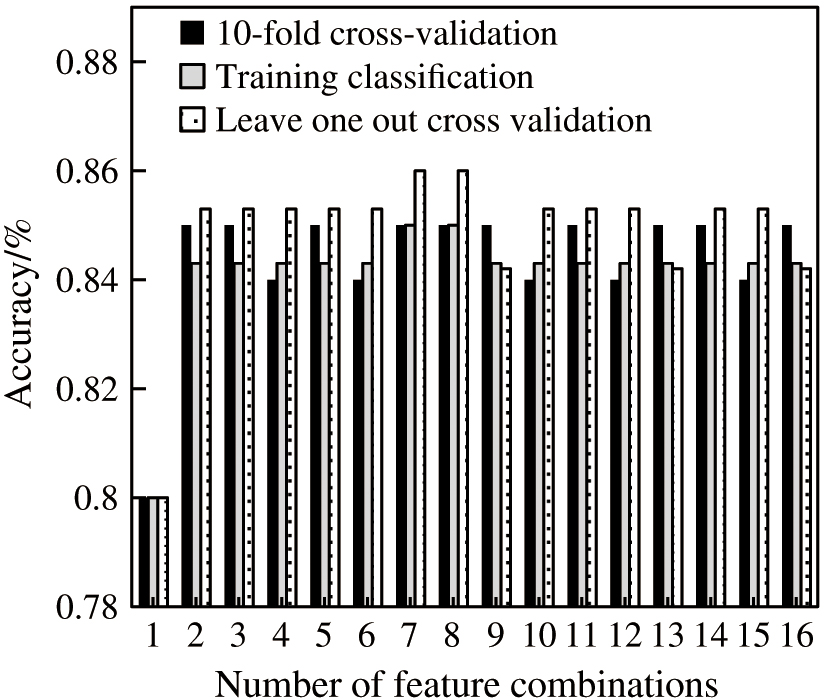Fig. 6. Accuracy of LR model under different number feature combinations.

2.VERIFICATION OF RF PREDICTION RESULTS

Based on the selected optimal subset, this paper describes the characteristics of solid electrolyte materials and utilizes random forest regression algorithm to predict the ionic conductivity of the materials. To verify the performance superiority of random forest regression algorithm in the aspect of classification prediction, RF random forest regression model constructed based on optimal subsets is compared with the constructed optimal LR model, k-Nearest Neighbor algorithm (KNN), Support Vector Machine (SVM), Adaboost algorithm, Gradient Boosting Machines (GBMs) and other classical classification models in the test data set [35]. The performance comparison results of the six models are shown in Table III:

Table III. Comparison of prediction effects of different models

Algorithm	MAE	MSE
LR	0.242	0.140
KNN	0.241	0.106
SVM	0.248	0.139
Adaboost	0.257	0.152
GBMs	0.244	0.138
RF	0.237	0.134

As shown in Table II, the mean absolute error and root mean square error of the six algorithms fluctuate between 0.23–0.25 and 0.10–0.15. Moreover, the error is relatively small, which proves that the optimal characteristics can describe the solid electrolyte material characteristics better.

The mean absolute error and root mean square error of the constructed optimal LR model are 0.242 and 0.14, respectively, and error results are slightly higher than those of RF and KNN models, but better than those of other models. This indicates that using logistic regression models can effectively capture the subtle relationship between solid-state electrolyte materials and ionic conductivity, demonstrating the feasibility of the proposed electrolyte material conductivity prediction method based on machine learning.

Furthermore, mean absolute error and root mean square error of the model using random forest regression algorithm are the lowest among the four algorithms, only 0.237 and 0.134, respectively. These results indicate that the conductivity error of solid electrolyte materials predicted by random forest regression model is minimal, which can more accurately find the solid electrolyte materials with higher ionic conductivity, and it proves the superiority of RF in predicting the conductivity of solid electrolyte materials.

3.CASE ANALYSIS OF MATERIAL PREDICTION

This study used K-means clustering method to classify materials with high ionic conductivity characteristics in the material library, and it uses the constructed optimal LR and RF models to predict the ionic conductivity of the material. Li40Ga8O32 and Li40Al8O32 are two solid electrolyte materials with similar spatial location and property characteristics. The constructed optimal LR model and the optimal RF model were used to predict the ionic conductivity of the two materials, and it was found that the high ionic conductivity measurements of the two materials were true. Among them, Li40Ga8O32 has been validated as a solid electrolyte material with good ionic conductivity in the research of scholars Liu Fenfen and Esaka, demonstrating the effectiveness of the constructed model. Therefore, it can be inferred that Li40Al8O32 with similar characteristics may also be a solid electrolyte material with good conductivity, which is worthy of further verification and analysis in the experiment.

VII.CONCLUSION

To sum up, the proposed conductivity prediction system for solid electrolyte material based on logistic regression algorithm and random forest regression algorithm firstly selected 18 kinds of feature descriptors that affected ionic conductivity from the material library. Then, this article utilized enumeration method, FSHD feature selection method, and Pearson coefficient to select feature combinations and reduce dimension. Finally, the logistic regression model and random forest regression model were constructed according to the optimal feature combination, and the ionic conductivity of the solid electrolyte material was predicted. The evaluation results showed that there were 7 feature descriptors, including the standard deviation of the average adjacency number of Li atom, the standard deviation of Li-X ionic bond, the average electronegativity of straight-line path, the average width of straight-line path, the average atomic volume, the average value of Li-Li bond and the packing fraction of the sublattice. In the evaluation of logistic regression models, it had the highest AUC value of LOOCV. The training accuracy, LOOCV classification accuracy, and average ten-fold cross-validation classification accuracy were high. In the evaluation of random forest regression model, the mean absolute error and root mean square error were smaller than those of classical classification models such as KNN, SVM and Adaboost. In addition, the ionic conductivity characteristics of solid electrolyte materials could be better described, so as to realize the rapid screening of solid electrolyte materials related to aluminum air batteries. The innovation of this paper was that it focused on the screening of performance index characteristics indicating high ionic conductivity in solid electrolyte materials and feature selection of high-dimensional small data through methods such as enumeration method and FSHD feature selection, which improving the performance of machine learning model on small-sample analysis, thus laying a foundation for the subsequent improvement of prediction accuracy of prediction models. The research deficiency lied in the fact that although the feature selection of high-dimensional and small data is realized, a small amount of data will still have some impact on the generalization and accuracy of the model. The next step of the research will refer to more studies on the ionic conductivity of materials to further expand the training sample size and increase the screening conditions that affect the performance to improve the accuracy of the model and to make the proposed method have a wider application space in the prediction of solid electrolyte materials.

Conductivity Prediction Method of Solid Electrolyte Materials Based on Pearson Coefficient Method and Ensemble Learning