I.INTRODUCTION

Paracetamol is one of the most widely used medications in the world [1]. The consumption of this drug is increasing rapidly every year. Besides being effective as painkiller [2], it is very reliable in the case of fever brought by viruses, colds, and flu.

Since the apparition of the COVID-19 pandemic, the paracetamol market has seen a big disruption. Thus, the market analysts must make informed forecasts about the paracetamol market and develop strategies to avoid losses. Indeed, it is extremely important to be able to make accurate forecasts of future sales in order to be able to calibrate the production process upstream [3]. Mastering these future sales plans, thanks to a good forecast, allows to plan the production, the availability of an optimal stock to meet market demand and especially to avoid the two extreme situations which can result from: the shortage of medicines or an overstocking that could lead to the expiry of the medicines [4,5]. Forecasting involves predicting the future as accurately as possible, taking into account all available information, including historical data and knowledge of any future events that could impact the result. To achieve this, data are time-dependent, and they refer to their sequences as time series [3]. Time series analysis is used to identify patterns and trends in historical sales data.

In this paper, a hybrid model is proposed to predict the sales of paracetamol. By employing time series decomposition, we can ascertain the patterns and fluctuations within our data. In our research, we utilize a two-phase approach. The aim of the first phase is to build a dataset of high quality because it is crucial for accurate data analysis. Indeed, wrong and aberrant data analysis may provide bad predictive results even with a powerful model, which may harm the organization, its customers, its partners, and patients. Anomaly detection helps to ensure that the data used for demand forecasting is complete and accurate. It reduces the risk of bias which leads to an improvement in the final results. However, it is important to consider the influence of imputing missing values on the final result and choose an imputation technique that maintains the original data pattern and structure. The second phase also has an important role for accurate data analysis, and it strongly affects the quality of the results. It turns into a forecast model that should be appropriate: the forecasting of pharmaceutical sales requires a model that exhibits low variability of performance, regardless of the specific time series being analyzed to have consistent and reliable predictions across different datasets.

The rest of the paper is organized as follows. Section II outlines the principal forecasting methods in the literature with a summary of previous research. After that, Section III presents our new forecasting approach, as well as the preprocessing methodology, anomaly detection, and missing data processing. Section IV presents the experimental results of our approach applied to paracetamol sales and its evaluation against the performance indicators and criteria. The conclusion is reported in Section V.

II.STATE OF THE ART

A.FORECASTING METHODS

Previous studies in the field of time series analysis demonstrate a variety of forecasting methods. In this section, we explore the most reliable of them.

First, Exponential Smoothing (ES) [6] is a time series forecasting technique in which data is linked exponentially over time by assigning weights that increase or decrease the data. It is suitable for time series with regular trends and fluctuations. However, the model does not work well for nonlinear time series, and it generally provides less accurate forecasts if the dataset includes strongly cyclical or seasonal variations. Triple Exponential Smoothing (TES), on the other hand, is used for time series showing both a trend and regular seasonality. However, it may not be appropriate for more complex time series. Moreover, TES model can be sensitive to outliers and extreme points, which can negatively affect forecast accuracy.

ARIMA [7] is a forecasting technique that uses a linear combination of past values and a series of errors to predict future values in a time series. It is capable of modeling variation processes, predicting trend movement and seasonal fluctuations fairly well. It is used for univariate, stationary, and nonstationary time series. ARIMA model is able to utilize training data derived from values observed over a short period of time. But when seasonality is important, this can lead to erroneous forecasts. This is due to the fact that ARIMA does not inherently account for repeating seasonal patterns.

Seasonal AutoRegressive Integrated Moving Average (SARIMA) [8] is based on ARIMA, taking seasonal elements into account. A SARIMA is formed by including additional seasonal terms to the ARIMA model. Although SARIMA is capable of modeling linear time series behavior, it is not suitable for nonlinear behavior. Moreover, when SARIMA uses training data over a short period of time, it may not accurately capture seasonal patterns, making performance forecasts poor.

Artificial neural network (ANN) [9] is a data-driven approach. Data is used to capture the relationship between input and output variables and to predict output values. ANNs are composed of a large number of highly interconnected processing elements (neurons) that work together to solve specific problems, such as detecting complex nonlinear relationships between dependent and independent variables. In practice, research works affirm that ANN model performance is better than statistical methods such as ARIMA and ES. Furthermore, the greatest advantage of ANNs is their ability to learn from large quantities of complex data. This can help reduce overfitting, as it provides more diverse examples from which the model can learn. However, the accuracy of ANN results is affected by noisy data.

A variant of ANN for forecasting is recurrent neural networks (RNNs) [10] which are able to identify and control nonlinear dynamical systems. In recent years, long short-term memory (LSTM) [3] surpass RNN because they use specialized memory cells and gating mechanisms to store information for longer periods of time. This allows capturing more complex temporal relationships in the data. LSTMs are suitable for time series data that are temporal or sequential in nature and of variable size.

On the other hand, fuzzy forecasting methods gain attention because they require fewer observations than many other methods. The fuzzy neural network (FNN) behaves as a universal approximator capable of soliciting human-interpretable (If-Then) rules used to forecast uncertain time series [11]. FNNs are robust to uncertainty and noise in the input data and can produce more accurate results for incomplete datasets, as they use fuzzy sets to represent the data. We can distinguish different types of FNNs.

First, fuzzy adaptive learning control network (FALCON) [12] uses a hybrid learning algorithm consisting of unsupervised learning to define the initial functions and the initial rule base using a conjugate gradient-based learning algorithm.

Adaptive Neuro-Fuzzy Inference System (ANFIS) [13] is the most used FNN and is a combination of an ANN and a fuzzy inference system (FIS). In forecasting problems, ANFIS models are well suitable to handle complex relationships and nonlinear models and can deal with missing or outlier data in the input. However, this can lead to poor model performance if these values are not properly handled.

B.RELATED WORKS

To achieve our goal, we review various studies related to sales time series forecasting. We will first look at work that predicts sales in general and then focus more specifically on pharmaceutical sales.

1)SALES FORECASTING

Sales forecasting constitutes a powerful and inevitable task for decision-makers in modern industry. An effective and reliable sales forecast in advance can help the decision-maker to estimate the amount and cost of production and inventory, and even to know the selling price, leading to lower inventory levels and achieving the just-in-time objective. For that, we can find in the literature many works for forecasting various types of data [14–17]. However, few works were dedicated to drug sales.

As mentioned in the previous section, there are a wide variety of forecasting techniques. Several studies showed that deep learning models give a performance in the sales market significantly better than shallow techniques. But the performance improved intensely with hybrid approaches when combining more than one forecasting model [18].

2)PHARMACEUTICAL SALES FORECAST

The work of Lakhal et al. [19] is notable among those devoted to forecasting pharmaceutical products. The objective of this work is to establish a good forecast of psychiatric drug sales in order to contribute to the production of realistic plans that meet market demand due to disruption after the outbreak of the COVID-19 pandemic. The experimentation shows a better accuracy for LSTM compared to ES, SARIMA, and SARIMAX.

The objective of [3] was to find the appropriate method to predict the consumption per month for six drugs: Ferrous Sulfat, Co-Trimoxazole, Amoxicillin, Clotrimazole, Amino-phylline, and Rifampin. To achieve this goal, the employed methods were ANN and Decision Tree (DT). After an empirical study, it has been found that ANN and DT are stable methods in this type of forecasting situation with a little improvement for DT.

Another work [5] selected two specific products which are Okacet (characterized by seasonal fluctuations in demand) and Stamlo Beta (not majorly subjected to seasonal fluctuations). The results show that TES works reliably for seasonal drugs, while moving averages perform better for nonseasonal drugs.

The work presented [20] describes the prediction of time series of brand and generic pharmaceuticals with various techniques. The brand name prediction of pharmaceuticals is performed using the ARIMA model, which is the most accurate model. On the other hand, the experimental results show that the long-term forecasts for generic drugs with Double Exponential Smoothing model are the most accurate.

Amalnick et al. [21] integrated clustering and classification techniques with neural network techniques to more accurately forecast product demand in pharmaceutical plants of 43 types of products. The main idea of the proposed approach is to cluster samples using K-means algorithm and elbow method and develop separate neural network models for each cluster to predict the demand in the pharmaceutical industry. The results indicate that clustering not only increases the accuracy of the forecast but also provides a more reliable assessment of the predicted values for each cluster. Finally, they have found that the multilayer perceptron neural network performs better compared to the other two models.

The objective of the work presented in [22] is to validate various shallow and deep neural network methods, with the aim of recommending sales and marketing strategies based on the seasonal trends/effects of eight anatomical and chemical treatment (ATC) thematic analysis groups. According to the results, the Demand Forecast Model (DFM)-based shallow neural network models performed well for five out of eight drug categories, while the ARIMA model performed best for the remaining three drug categories.

III.THE PROPOSAL: SALES FORECASTING OF PARACETAMOL PRODUCTS

The aim of this paper is to establish a good forecast of paracetamol sales in order to contribute to the production of realistic future sales plans that meet the market demand. To achieve the goal, we explore the possibility of building a dataset with high quality in addition to choosing appropriate techniques because poor analysis can result from various factors beyond data quality, such as the application of unsuitable techniques, and making a decision based on wrong information may harm the organization, its customers, its partners, and patients. Figure 1 presents the process of our proposal which is comprised of three steps:

  • 1)Anomaly Detection: this step involves identifying anomalous data points in the dataset.
  • 2)Data Imputation: the next step is to impute or replace anomalous values with appropriate estimates.
  • 3)Forecasting: this step is to use the cleaned and imputed data for forecasting of paracetamol products.

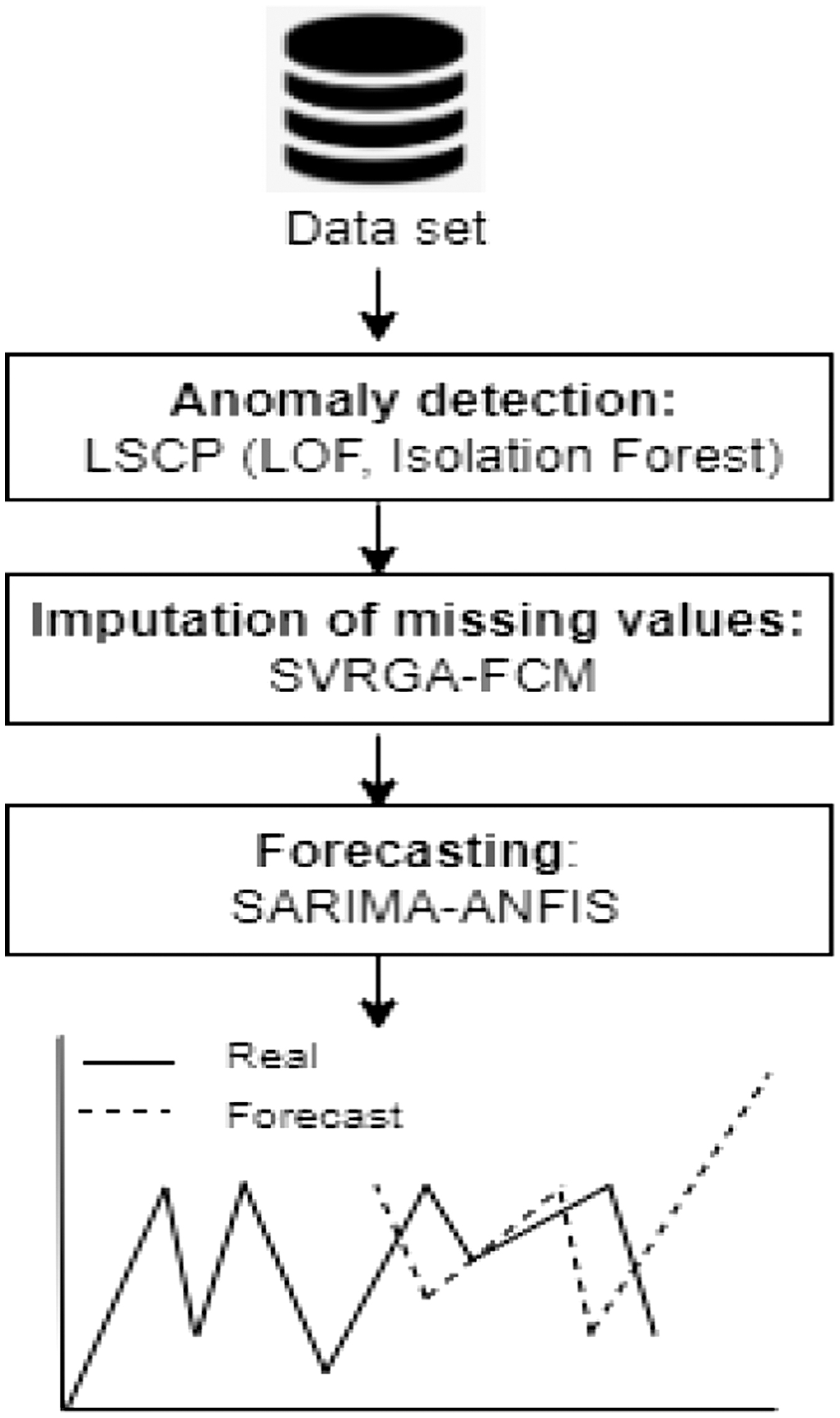Fig. 1. Global process of methodology.

A.OUTLIER DETECTION

Anomaly Detection in Time Series Data deals with identifying anomalies in data that have a temporal component, such as sales that do not conform to clearly defined behavior or deviate from most observations. Local Outlier Factor (LOF) [23] is an algorithm for finding anomalous data points by measuring the local deviation of a data point from its neighbors. It is one of the algorithms for detecting local outliers in datasets with complex and irregular structures. Moreover, Isolation Forest [24] is particularly useful for detecting outliers in high-dimensional datasets with a relatively small number of samples and can handle various types of outliers.

To benefit from the advantages of Isolation Forest and LOF, we use a combination of them using Locally Selective Combination in Parallel Outlier Ensembles (LSCP) [25]. This method first utilizes Isolation Forest to scan the dataset, prunes the apparently normal data, and generates an outlier candidate set. Then LOF is applied to further distinguish the outlier candidate set and get more accurate outliers. The proposed ensemble method takes advantage of the two algorithms. Moreover, it is computationally efficient and can be used in real-time and streaming applications.

Isolation Forest works on the principle of decision trees. This algorithm isolates outliers by randomly selecting a feature and then randomly selecting a split value between the maximum and minimum values of the selected feature. Anomalies are the points that have the shortest path in the tree. By “path,” we mean the number of branches to cross from the main node.

An equation defines the anomaly score assigned to each observation x which is the following:

s(x, n)= 2−E(h(x))c(n)
with n the number of external nodes, h(x) the path length of the observation x, the expression E(h(x)) represents the expected or “average” value of this path length across all the Isolation Trees, and c(n) the average path length of the unsuccessful searches in the binary search tree. The anomaly score will always be between 0 and 1, so it is quite similar to a probability score. Each observation receives an anomaly score and based on this score we can make the following decisions:
  • •A score s(x, n) close to 1 indicates an anomaly.
  • •A score s(x, n) below 0.5 indicates a normal observation.

After that comes the stage of LOF algorithm. To understand LOF, we need to understand some other concepts:

  • -K-distance is the distance between the observation and its kth nearest neighbor. K-neighbors are groups of observations within a circle of radius K-distance.
  • -K-neighbors is a group of observations within a circle of radius K-distance.
  • -Reachability Density (RD) defines the maximum between the K-distance of Xj and the distance between Xi and Xj, where Xi and Xj are two points in the dataset.
  • -Average Reachability Distance (ARD) is a measure of the average distance between a data point A and its neighboring point with the highest density.
  • -Local Reachability Density (LRD) is the inverse of ARD. It is obtained by the following formula:
    LRD (A)=1∑Xj∈NKRD (A, Xj)||Nk(A)||
    with Nk(A) the set of k nearest neighbors of point A. According to this formula, the greater the ARD distance (the farther the neighbors), the less point density is presented around a particular point. Low values of LRD imply that the nearest cluster is far from the point.

Then, LOF is determined as follows:

LOFk(A)=∑xj∈NkLRD(Xj)||Nk(A)|| 1LRDK(A)

Generally, if the LOF value is greater than 1, the point is considered an outlier.

B.DATA IMPUTATION

After detecting outliers, the step of imputation of missing values comes to estimate these values in order to increase the quality of the data. We choose to use a hybrid method [24,26] that combines a reliable machine learning technique known as support vector regression (SVR) and a genetic algorithm (GA) with fuzzy C-means (FCM). Figure 2 illustrates the process of this phase.

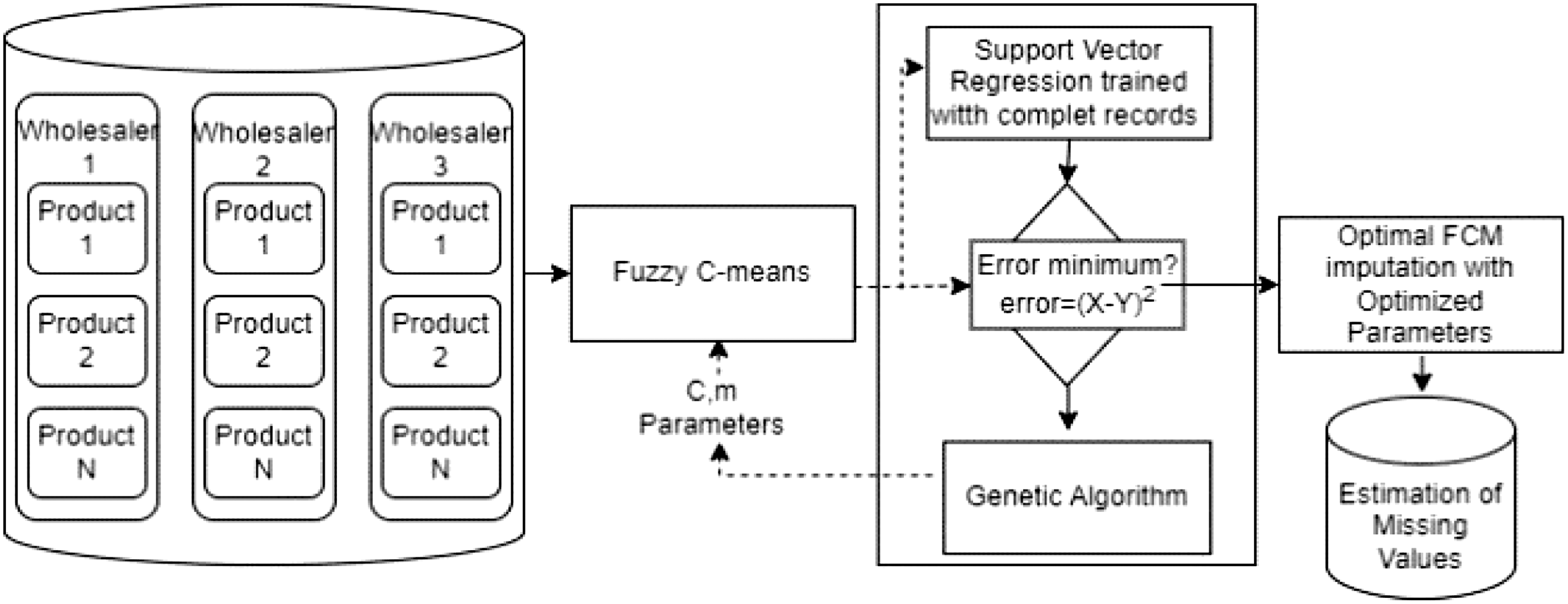Fig. 2. Imputation of missing values.

The FCM algorithm is a clustering method that allows data points to belong to multiple clusters, assigning membership values to indicate the degree of belongingness to each cluster. When dealing with missing values, one approach is to assign the value of the cluster centroid to which the corresponding data point belongs. This means that for each missing value, we can replace it with the value of the centroid that has the highest membership degree for that data point. This process is repeated for all incomplete rows for each wholesaler and product in the dataset to create a complete dataset with imputed values for missing entries.

After the missing values in the incomplete rows are estimated using FCM, we train SVR with complete records, that is, data where all values are present. Then, the output of FCM is compared to the SVR output vector. This comparison is important because it allows us to evaluate the accuracy and reliability of the imputed values. If the output of FCM is very different from the SVR output vector, this could indicate that the imputed values are not accurate or reliable.

The principle of the adopted method is to optimize FCM parameters. Optimized parameters C and m of FCM are obtained by using the GA. The aim of GA is to search the parameter space for values of C and m that minimize the difference between the SVR output and the FCM output. This way, we can ensure that the imputed values are as accurate and reliable as possible and that the FCM algorithm is using the best possible parameters for the given dataset.

C.FORECASTING

As mentioned in the state of the art reported in this study, each forecasting method has its own properties. In time series applications, it is almost impossible to know in advance which forecasting model will work best for a dataset. This corresponds to the recognized fact that no single model is best for all situations and circumstances.

For this reason, the meaning of “best” can be interpreted in different ways, such as the best model whose predictions work well and have low variability in performance, regardless of the time series being analyzed. Due to the complexity of nonlinear structures, this paper proposes a combinatorial approach as an effective way to improve performance prediction.

In fact, we have concluded from our literature review that using a single model is more likely to yield inaccurate predictions than using a combination technique. The purpose of combining the models is due to the assumption that a single model cannot define all time series characteristics. This finding indicates that combining forecasts is less risky than choosing a single forecasting model.

As mentioned earlier in this paper and in our previous works, SARIMA is able to produce satisfactory predictions for linear time series data, but it is not suitable for the analysis of nonlinear data. Since the SARIMA model cannot capture the nonlinear structure of the data, the residuals of the SARIMA model are expected to contain information about the nonlinearity. The residuals represent the unexplained variation in the data after taking into account the linear patterns modeled by the SARIMA model and seasonal variations. This is due to the fact that SARIMA models are designed to capture underlying trends and seasonality in time series data.

Hence, ANFIS models are well suited to handle complex relationships and nonlinear patterns and can deal with missing or aberrant data. Indeed, it is a nonlinear model that is often more resistant to outliers and noise due to its adaptive nature. By modeling residuals using ANFIS, we aim to extract and capture nonlinear relationships present in the data that a linear model might miss. This can lead to more accurate forecasting and modeling of time series data.

We can conclude that the most reliable combination is the hybrid SARIMA-ANFIS method which combines the strengths of both methods and can handle both seasonality and complex patterns in the data, providing more complete predictions than either method alone.

After preprocessing, once we have identified and imputed missing values, we can use our cleaned-up dataset as input of our predictive model. We split our time series data into linear and nonlinear forms. Figure 3 presents the architecture of our hybrid forecasting method. The process of combining ANFIS and SARIMA models involves first obtaining the predicted values from the ANFIS and SARIMA models in parallel.

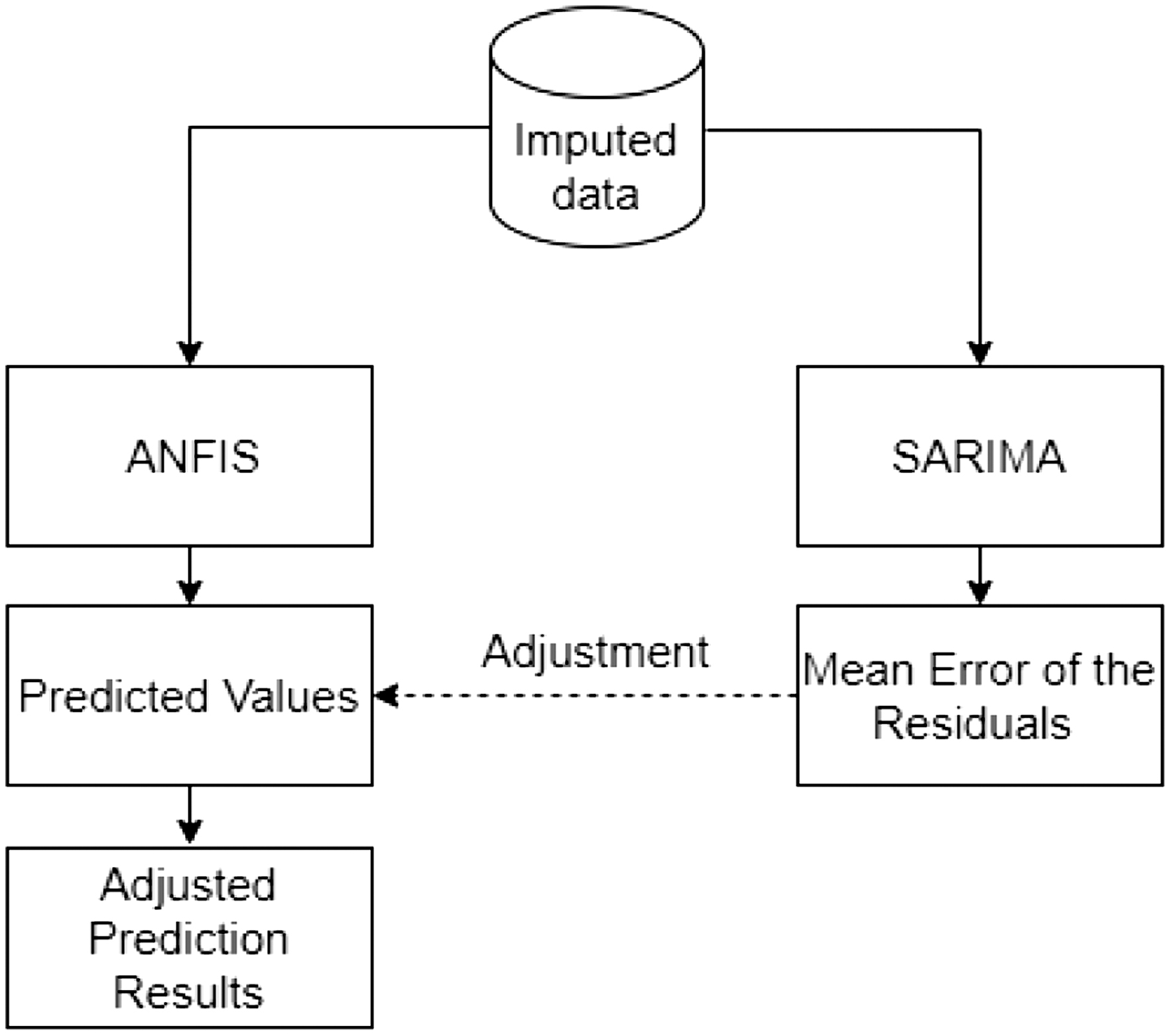Fig. 3. Architecture of our hybrid forecasting method.

Then, we calculate the mean error of residuals from the SARIMA model. The residuals represent the differences between the actual values and the predictions made by the SARIMA model. By averaging these errors, we obtain an estimate of the systematic bias or error observed in the SARIMA predictions. Finally, we combine the mean error of residuals with the predicted values from the ANFIS model. This adjustment serves to account for the errors captured by the SARIMA model, effectively improving the ANFIS predictions by aligning them with the average error observed in the SARIMA residuals.

1)SARIMA

In order to apply SARIMA, we use some parameters such as:

  • •Seasonal periods: it sets how many periods with seasonality our model has, in this particular case, two spikes of seasonality; therefore, it was set to 2. The choice of a seasonal period in time series analysis often depends on analyzing the autocorrelation function (ACF) graph and observing of the seasonal decomposition of the time series. By plotting the time series data using decomposition of the time series technique, we detect periodic patterns of two distinct peaks within a period, indicate a seasonality of 2. Moreover, when interpreted the result of ACF, there are peaks at lags 6, and this could confirm half-yearly seasonality that suggests a potential seasonality of two periods.
  • •Enforce stationarity: it helps our model to transform the AutoRegression parameters in order to insure stationarity.

Our SARIMA model comprises four iterative steps:

  • a)Identification: this step involves the selection of nonseasonal autoregressive order (p), nonseasonal moving average order (q), and differentiation order (d). Correspondingly, (P, D, Q) denotes the representation of each part of the sequence after making a seasonal difference. (P): seasonal autoregressive order, (D): seasonal differentiation order, and (Q): seasonal moving average order using autocorrelations (AC) and partial autocorrelations (PAC).
  • b)Estimation: historical sales data are used to estimate the parameters (p,d,q) (P,D,Q) of the SARIMA model identified in step 1.
  • c)Calculation of the residuals: the residuals represent the differences between the actual values and the SARIMA predictions.
  • d)Calculation of the mean error of residuals: this step takes the average of the residuals obtained. This value represents the systematic bias or error observed in the SARIMA predictions.

2)ANFIS

The architecture of our ANFIS model is shown in Fig. 4, where we can see different layers of ANFIS which have different nodes. The square nodes are for adaptive nodes with parameters and the circular ones are fixed nodes without parameters. The number of membership functions for every input is a hyperparameter that is tuned during the model training process. Our ANFIS model is being initialized with three inputs and three membership functions for each input. Indeed, these hyperparameter values are capable of modeling a wide range of nonlinear relationships between the input variables and the output variable.

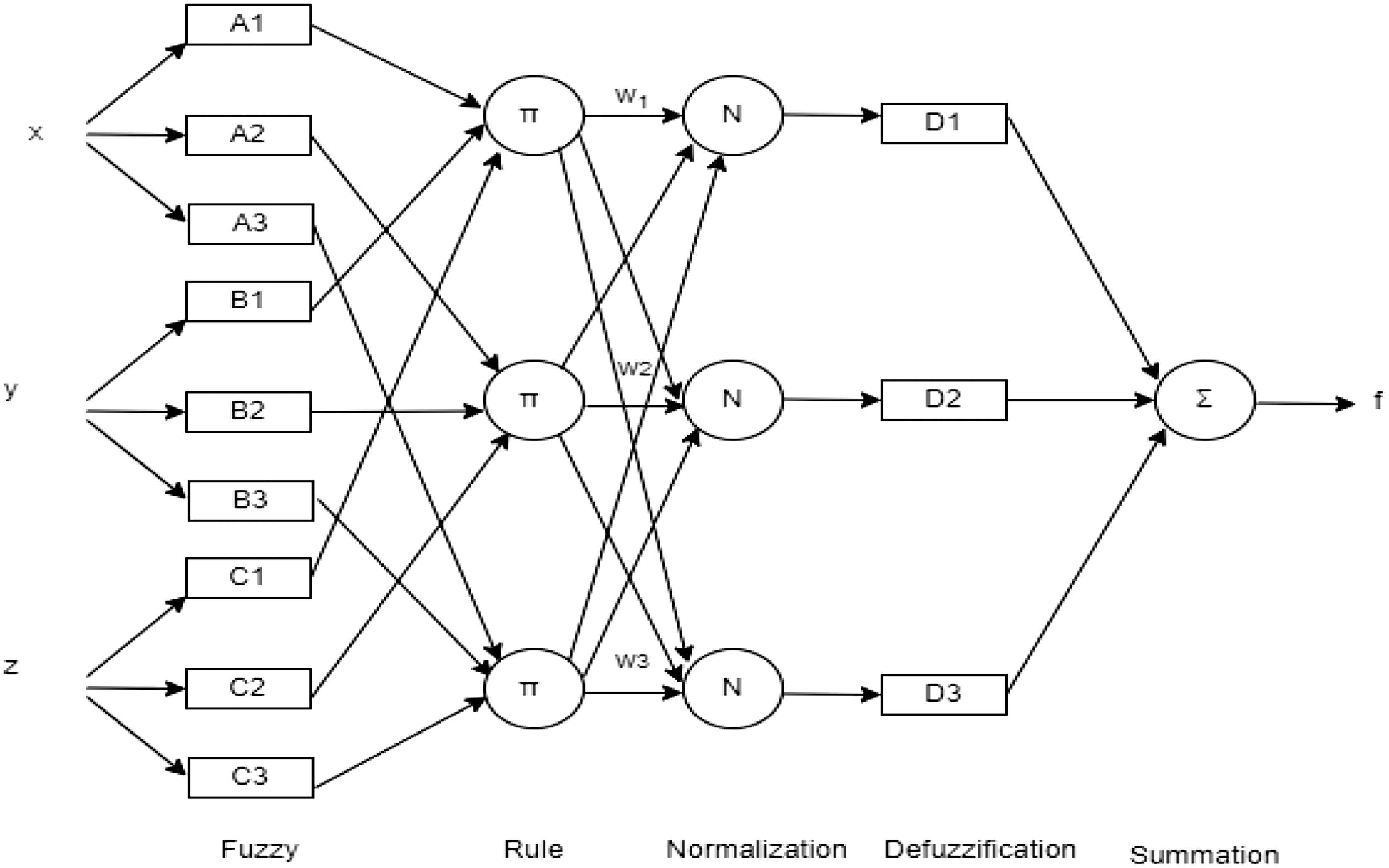Fig. 4. ANFIS architecture with three inputs and three rules.

We use the Random Forest Regressor [27] to determine feature importance and select the most relevant features to be used as inputs for the ANFIS model. The total number of regressors in the ANFIS model is calculated as the product of the number of membership functions for each input.

Our ANFIS is composed by:

  • •Fuzzy Layer: It is responsible for computing the membership degree of each input data point to each fuzzy rule.
  • •Rule Layer: It consists of nodes that calculate the firing power of each rule in the fuzzy rule base.
  • •Normalization Layer: It is responsible for scaling the output values of the fuzzy layer to ensure that they fall within certain criteria.
  • •Defuzzification Layer: It is responsible for converting the fuzzy outputs into crisp values.
  • •Summation Layer: It is a type of layer where the output of each neuron is summed up to create a single output value for the layer.

3)Predictive result

We decompose our time series data into linear and nonlinear components at time t using the following formula:

y[t]= L[t]+N[t]
where L[t] shows the linear component of the time series, while N [t] shows the nonlinear components.

Initially, we predict the values of the linear components in the time series using SARIMA and the nonlinear components in the time series using ANFIS model. Then SARIMA and ANFIS predict the values of the linear and the nonlinear components, respectively. After, the residual is calculated by subtracting the predicted SARIMA values from the actual values of the time series. The data that are not considered in the linear prediction of the SARIMA model are the residuals, which represent the nonlinear components of the data. Thus, the residuals are obtained by the following equation:

residual[t]= y[t]−Lpredict[t]
where Lpredict[t] are the predicted values of the SARIMA model.

After, we calculate the mean error of the residuals in the SARIMA model by determining the average of the residual values using mean absolute error (MAE):

SARIMAerror(t)=(1/n)*∑|residual[t]|
where n indicates the number of observations.

Finally, we combine the residuals from the SARIMA model with the predicted values from the ANFIS model to improve the performance. The prediction equation that describes the result is as follows:

ypredict[t]= Npredict[t]+SARIMAerror[t]
where Npredict[t] are the predicted values of the ANFIS model. This combination allows the ANFIS model to focus on predicting the nonlinear component of the time series, while incorporating information from the SARIMA model’s residuals to improve the accuracy and performance of the ANFIS predictions.

IV.EXPERIMENT AND RESULT ANALYSIS

We analyze in this study the data of paracetamol drugs sales collected from pharmaceutical wholesalers from January 2019 until June 2023 as shown in Fig. 5a. Selected drugs of paracetamol from the dataset are FERVEX Ad. S.Sucre Pdre Pdre.Sol.Or Bt 8Sach./5gr, EFFERALGAN 1gr Comp.Efferv. Bt 1Tb/8, and NOVADOL 1000 mg Comp. Bt 8. We note in the dataset that there are other paracetamol drugs (like EFFERALGAN 330 MG VIT C B20 EFFERALGAN 600MG SUPP B/10, EF- FERALGAN 80MG SUPP NN, EFFERALGAN ENF 300 SUPP, EFFERALGAN PED 90 ML, EFFERALGAN SUPPENF 150MG…). However, they are not marketed in this period, or they face disruptions in their production. Thus, their data are not stable, and we cannot consider them in this study.

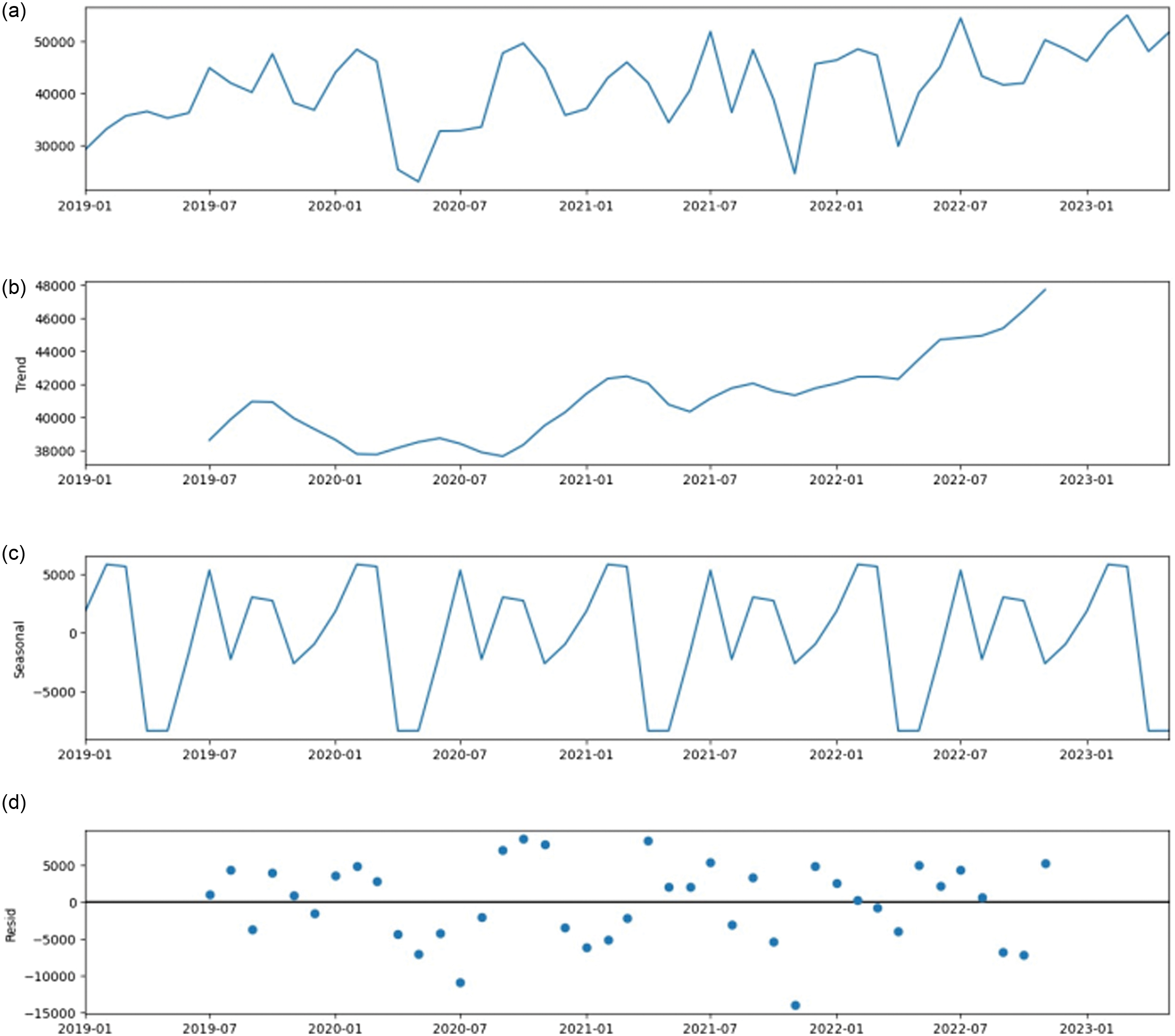Fig. 5. Decomposition of the time series.

We have a dataset containing the sales month by month during this period. Thus, our data are represented as a monthly time series. We first need to determine the major characteristics of the time series. We focus on the trend, seasonal, and residual components of our data. Trend, as its name indicates, is the overall direction of the data. Seasonality is a periodic component that exists when a series exhibits regular fluctuations based on the season (e.g., every month/quarter/year). Ideally, trend and seasonality should capture most of the patterns in the time series. Hence, the residual is what is left over when the trend and seasonality have been removed. We can notice that the sales change and that the time series is clearly not stationary. Thus, the main objective of seasonal time series analysis is focused on periodical fluctuations and on its interpretation. As shown in Fig. 5(b) and (c), the detection of the characteristic of its time series has seasonality issues and our trend is neither constant nor linear.

In this work, the second step is outlier detection of the dataset using LSCP. A label is used as a result indicating whether an instance is an anomaly or not, and a score or confidence value as a more informative result indicating the degree of anomaly.

The next step of common approach in data preprocessing is to treat the anomaly data as missing data and to impute them. The method we use is the combination of FCM and a GA with SVR. By making several tests, we deduce that the MAPE of FCM-GA-SVR is better than the MAPE of SVR-FCM without GA, which means that the SVR-FCM-GA approach has better predictive accuracy than SVR-FCM without GA. Using GAs in FCM-GA-SVR optimizes the parameters of FCM and SVR models and improves data imputation performance.

Finally, we develop forecasting models which are TES, SARIMA, ANFIS, LSTM, and SARIMA-ANFIS, and we compare the results obtained by the five techniques. We find the optimal combination of parameters for TES by following an iterative minimization approach of MSE. Moreover, we use grid search to optimize the LSTM and automatically adjust the hyperparameters which are batch size, learning rate, epoch, and regularization of dropouts. The model exhibits satisfactory convergence, and there is neither overfitting nor underfitting. This indicates that the model can produce accurate predictions and is well fitted.

In order to reduce the execution time for anomaly detection, we use joblib which allows a parallel run of tasks. Moreover, for data imputation, we use the multiprocessing Apache spark solution, which enables us to work on large volumes of data without increasing processing times. After, we adopted the RAPIDS library to optimize the execution time of our approach, which is designed to accelerate data processing. In addition, it can help reduce execution time by using the computing power of GPUs to perform operations faster than CPUs. For model monitoring, we use callbacks, which are functions offered by Tensorflow to monitor the model during the learning phase in order to keep the best model without overfitting.

To find the optimal parameters for the SARIMA model, we perform our model by choosing the parameter combination with the lowest root mean squared error (RMSE). After, we fine-tune the model of ANFIS by adjusting its hyperparameters and by using techniques such as early stopping to improve the model’s performance.

To validate the accuracy of the predictions, we use MAPE which is the mean or average of the absolute percentage errors of the predictions. The main benefit of using MAPE is that it penalizes large errors. It also scales the scores in the same units as the forecast values (i.e., per month for this study). Models with smaller MAPE values perform better. The formulas of the MAPE indicator are as follows:

MAPE=100N∑i=1N|yt−y^tyt¯|
where N is the total number of observations, yt is the actual value, y^t is the predicted value, and yt¯ is the average of the entire prediction resultant value.

Now, we proceed to compare results, for analyzing the efficiency of the models using MAPE. We can see in Table I the MAPE of the five models that we performed in this work: TES, SARIMA, LSTM, ANFIS, and SARIMA-ANFIS.

Table I. Error measurement MAPE

DrugsTESSARIMALSTMANFISSARIMA-ANFIS
FERVEX59382716227
EFFERALGAN45132343627
NOVADOL4830296219

We notice from this table that SARIMA and TES give a bad forecasting result for EFFERALGAN. This is caused by the nonlinear character of EFFERALGAN data. Moreover, we can see that the result of ANFIS and TES is not satisfactory for FERVEX. In fact, the data of FERVEX are too high noisy. However, ANFIS and TES model are unable to give a good performance of forecasting in this situation, which explain these bad results. For those reasons, we consider that the models TES, SARIMA, and ANFIS are not suitable for forecasting paracetamol sales. On the other hand, LSTM is stable for all the studied paracetamol drugs. Finally, the proposed SARIMA-ANFIS model has the lowest testing MAPE value for all products, which proves that our hybrid model is the best among the considered models.

Forecasting sales is a complex task, and any forecast will contain a degree of uncertainty. It is important to have up-to-date data and continuously monitor actual sales to see how well the model is performing and make adjustments as needed. The hybrid model ANFIS-SARIMA outperforms TES, SARIMA, LSTM, and ANFIS models in terms of forecasting accuracy. Our model gives good results despite the replacement of missing drugs by generics in coordination with doctors to find an alternative method of treatment.

V.CONCLUSION AND FUTURE WORK

The objective of this study is to develop a time series forecasting model for predicting paracetamol drug sales. The time series data of paracetamol drugs has been analyzed, and anomalies were identified using LSCP. Data has then been imputed using SVR and GA with FCM. Finally, the next month’s sales have been forecasted using TES, SARIMA, LSTM, and ANFIS models and then with a new hybrid model SARIMA-ANFIS. The aim of our hybrid model is to leverage the nonlinear predictions of ANFIS while incorporating the adjustment based on the SARIMA model’s error characteristics. After conducting various tests, we have found that the SARIMA-ANFIS hybrid model has the most promising results. Based on these results, it has been concluded that our hybrid approach enhances the overall accuracy of the predictions. Further optimization of the model’s execution time is planned for future work. Moreover, we plan to try out the model with other pharmaceutical products.