I.INTRODUCTION

Data representation and its graphical visualization for knowledge processing tasks are one of the major tasks by research communities [1,2]. In this regard, the Euclidean geometry [3] and its postulates help a lot while drawing point, straight line, circle, rectangle, or parallel lines [4]. It provided a famous theorem that the angle sum of a triangle must be 180° as shown in Fig. 1. In a similar way, the famous Pythagorean Theorem, i.e. a2+b2=c2, is also one of the most potential examples of Euclidean geometry as shown in Fig. 2.

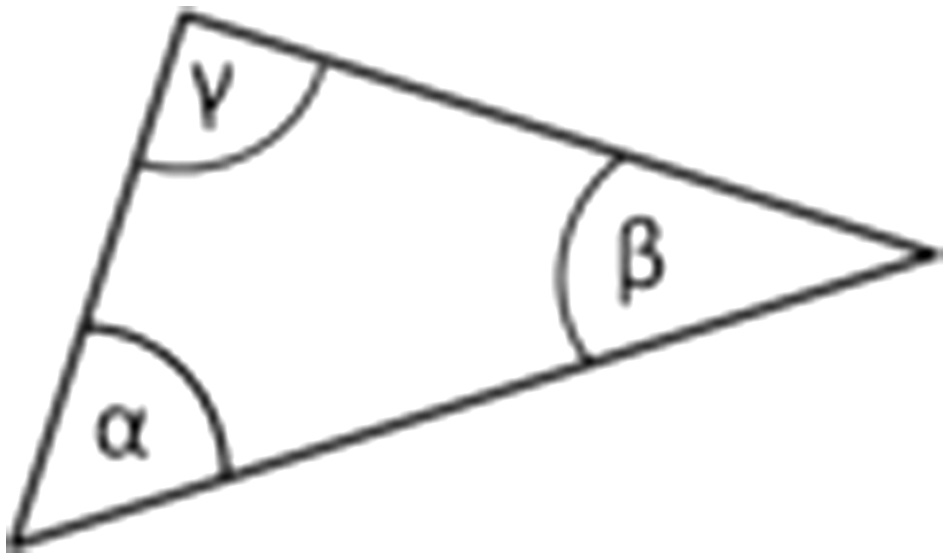Fig. 1. The sum of angle in the given triangle is 180° as per Euclidean geometry

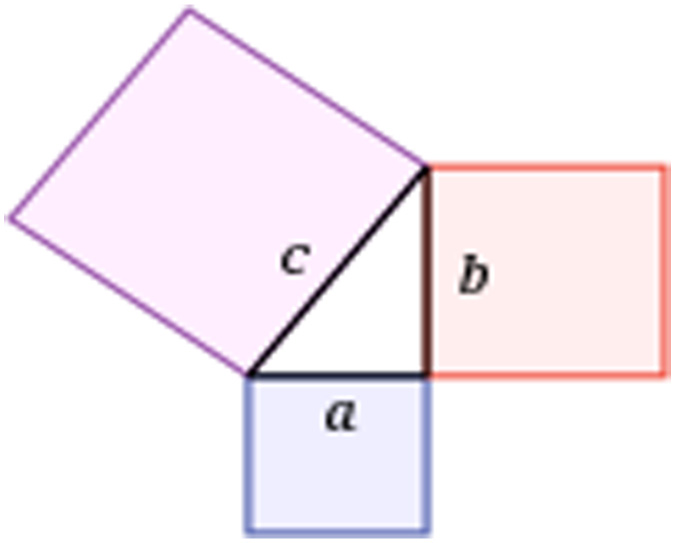Fig. 2. The Pythagorean theorem which stated a2 + b2 = c2 using Euclidean geometry

The problem started with Euclidean geometry while dealing with the rectangle having nonplanar shape as shown in Fig. 3 [5].

Fig. 3. An example of non-Euclidean geometry

It gives a way to reinvestigate the Euclidean postulates which were done by Gauss (1775–1855), Lobachevsky (1792–1856), Bolyai (1802–1860), and B. Riemann (1826–1866) [6]. They found vagueness in Euclidean parallel postulates that one and only one parallel line can be drawn from a given point not on the straight line. They tried to prove it via negation of these postulates. Lobachevsky (1792–1856) and Bolyai (1802–1860) tried to draw more than one parallel line from a point not on the straight line as shown in Fig. 4 [7–9]. It is defined as Smarandache geometry [10–12]. Recently this theory is extensively studied using NeutroAlgebra [13–15] to visualize them via NeutroGeometry [16–18].

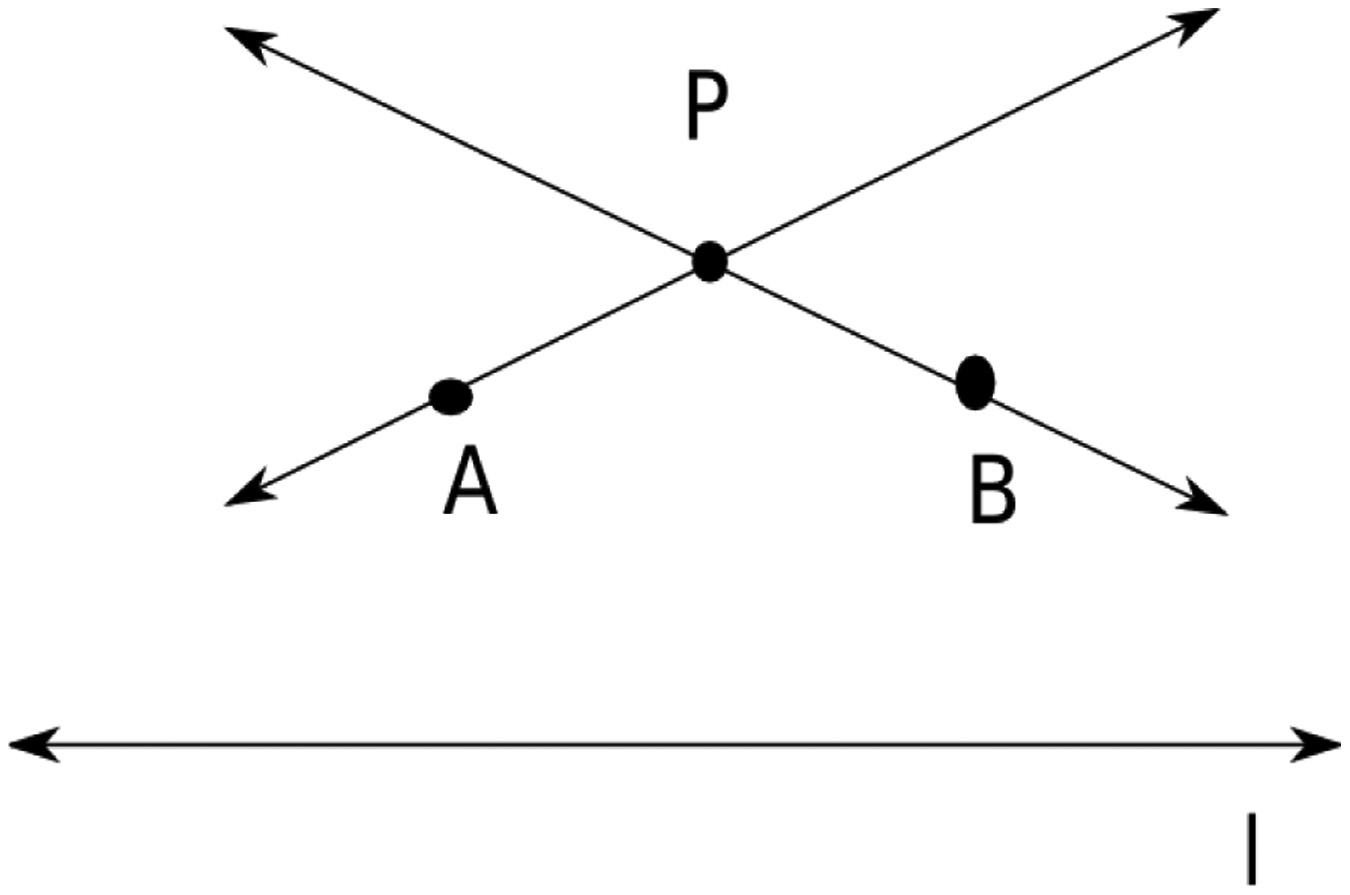Fig. 4. The alternative of Euclid parallel postulates

It means the traversal from A to B and B to A cannot be the same in non-Euclidean geometry. It used to depend on the positional momentum of element in the space and its changes with respect to time. It can be understood as an example that you want to walk on a defined path to till its End. You become tired after some time and feel emptiness due to which start traveling halfway, before you get halfway started quarter then one-eight, one-sixteen, and so on. It will require infinite number of paths to complete. These types of non-commutative geometry where AB and BA do not apply need attention for precise analysis using some non-Euclidean geometry [7,8]. This happened with human cognition when several parallel paths exist from a given point not the straight line as shown in Fig. 5.

Fig. 5. The three parallel lines from a given point not the straight line

In this case, the problem arises while dealing with the human cognition and its quantum state which depends on conscious and unconscious mind as discussed by Nāgārjuna [19,20]:

  • (i)Both lines exist in the given space from the point.
  • (ii)No line or path exists in the given space from the point.
  • (iii)Either lines (or paths) exist or does not exist at the same time.
  • (iv)Both do not exist or empty.

It creates an emptiness in mind to walk or not in quantum state as follows:

  • (i)These lines (or parallel paths) can be produced by themselves, or
  • (ii)They can be produced from other things, or
  • (iii)They can be produced from both themselves and from other things, or
  • (iv)They cannot be produced from any ways.

To deal with these types of human cognition containing superconscious truth or Turiyam State, non-Euclidean geometry and its algebra is required [16–18]. Even the hierarchical order visualization of any data sets in tree or graph also requires non-Euclidean geometry. The reason is that these types of data set require exponential (2n) vertex and its visualization for n items [21]. It needs non-Euclidean or exponential space to analyze the data in case of large amount. It is indeed a requirement as per current scenario. To achieve this goal, this paper tried to focus on introducing some new concepts of non-Euclidean geometry and its real-life examples for further study.

Other parts of the paper are structured as follows: Section II provides some data with non-Euclidean geometry and its visualization. Section III proposed a method for characterization of non-Euclidean geometrical data sets. Section IV provides some of the real-life examples for non-Euclidean geometry and its applications in knowledge processing tasks. Section V provides conclusions followed by acknowledgment and references.

II.NON-EUCLIDEAN GEOMETRY

This section provides some examples to understand the non-Euclidean geometry as given below:

In this section, some non-Euclidean geometry and its visualization are shown for better understanding.

Definition 1. (Types of Geometry) [22]:The first issue arises with any researchers about the difference between Euclidean and non-Euclidean geometry and its visualization. To achieve this goal, Fig. 6 represents the difference between hyperbolic, Euclidean, and elliptic geometry [4–8]. Now the non-Euclidean drawing shown in Fig. 3 can be visualized using the hyperbolic space.

Definition 2. (Spherical Geometry) [23]:It is a geometry of solid. In this geometry, the triangle postulates as well as Pythagorean theorem fails as shown in Fig. 7. The sum of the angle of a triangle in spherical geometry is not 180°. Same time, all three sides have the same length which means a2 + b2=c2 does not apply in spherical geometry [24].

Definition 3. (Hyper Geometry) [17]:it provides the failure of parallel postulates that many lines can be drawn from a point outside the given line. Same time the hyperbolic geometry rectangles differ from Euclidean rectangles as shown in Fig. 8. It means this geometry contains more saddle points which look like equilibrium. This type of geometry is helpful in finding heteroclinic orbital path and periodic strings in the given language.

Definitions 4. (Systolic geometry) [25]:This geometry describes the relationship between the area inside a closed curve and its perimeter. It forms isoperimetric inequality when the area is less but the perimeter is longer as per Euclidean Postulates as shown in Fig. 9. One of the real-life examples is a drop of water on a leaf and its shape. The drop of water is used to form a symmetric round shape with a fixed amount of water. It happens due to surface tension and its forces which minimize the surface area for the drop and form a round sphere as shown in Fig. 10.

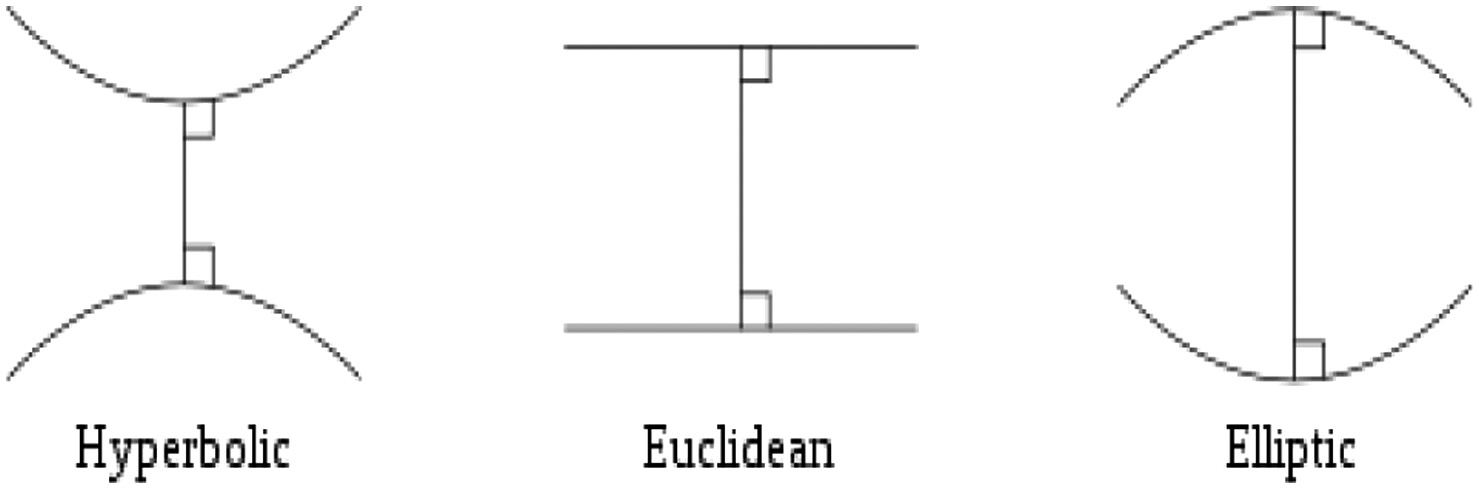Fig. 6. The difference between Euclidean and non-Euclidean geometry (hyperbolic and elliptic)

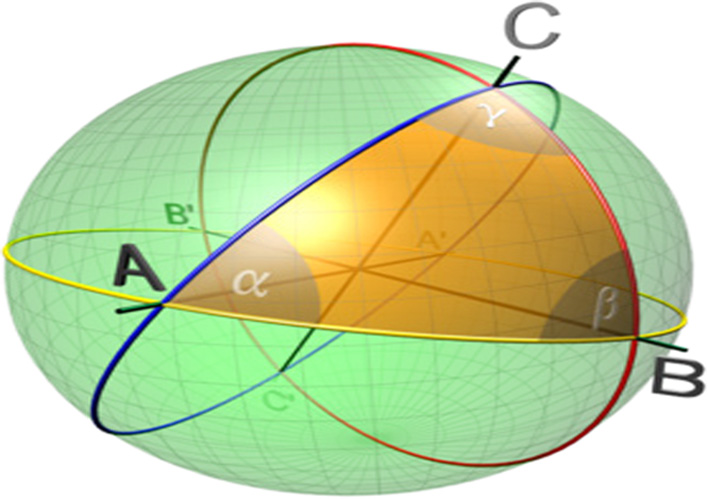Fig. 7. The examples for the negation of Figure 1 and 2 of Euclidean geometry

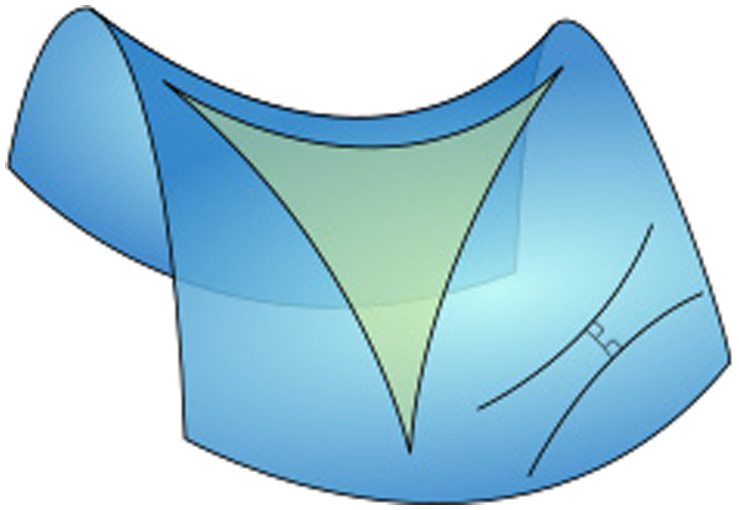Fig. 8. A triangle immersed in hyperbolic paraboloid with two diverging ultra-parallel lines [39].

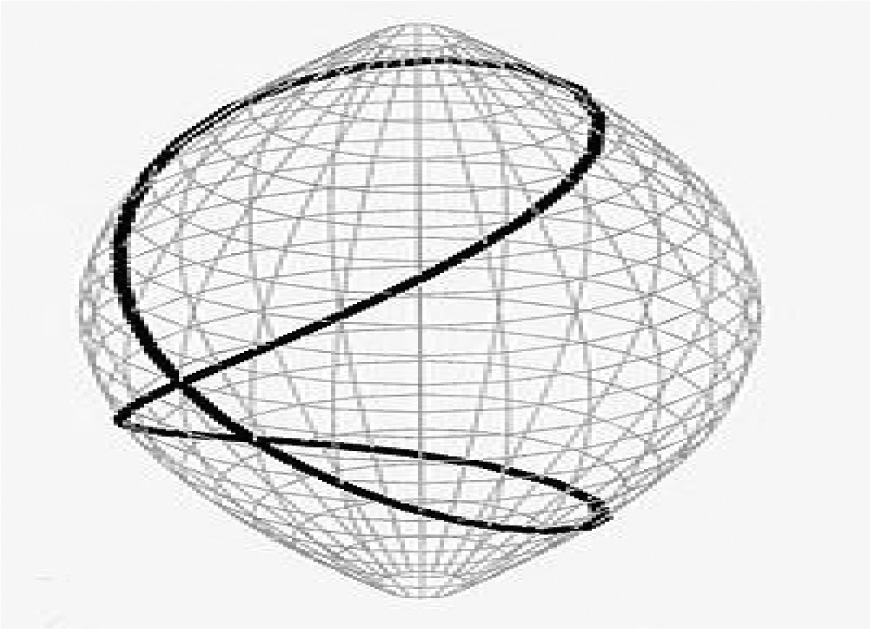Fig. 9. The systolic geometry and its visualization using a geodesic on a football

Fig. 10. A isoperimetric inequality and its formations by drop of water

How to deal with these types of physical phenomenon and characterize them in true, false, or uncertain regions is one of the most crucial tasks. In the next section, a method is proposed to deal with these types of data in NeutroGeometry for multidecision process [26].

III.A METHOD TO DEAL NON-EUCLIDEAN DATA

In this section, a method is proposed for characterization of non-Euclidean data in true, false, and NeutroGeometry as follows:

  • Step 1. Let us consider the data with non-Euclidean geometry and its attributes (A).
  • Step 2. Let A be any non-empty set of a given Non-euclidean geometrical data.
  • Step 3. Define the operator as :○:A×A→Pn(A) As (T,I,F)∉{(1,0,0),(0,0,1)}.
  • Step 4. In case any map is possible, then we can characterize them as follows:
    • (i)In case any element of x,y∈A, non-Euclidean geometry provides a new element in non-Euclidean geometry, i.e., x ○ y ⊆ A. It can be considered as true characterization.
    • (ii)In case any element of x,y∈A, non-Euclidean geometry provides a new element which does not exist in the non-Euclidean geometry using the given operator as x ○ y ⊈ A. It can be considered as false regions.
    • (iii)In case any element of x,y∈A, non-Euclidean geometry provides a new element which in saddle space and its quantum state is uncertain. This type of element can be considered in NeutroGeometry.
  • Step 5. It defined a function f: XY, which provides three possibilities:
    • (i)In case a well-defined mapping exists among X and Y, then it is called as true regions.
    • (ii)In case the mapping is undefined or outer-defined mapping between X and Y, then it is in false regions.
    • (iii)It is unknown whether the mapping exists or not and what is the value for the mapping among X and Y then the element is in NeutroGeometry.
  • Step 6. In this way, the non-Euclidean data sets and its characterization can be possible.
  • Step 7. The similarity among the data sets can be found using the Geodesic distance.
  • Step 8. The geodesic distance provides the shortest path among two non-Euclidean data rather than its straight line distance of Euclidean geometry as shown in Fig. 11.
  • Step 9. The data closed to the defined geodesic distance can be considered as Cluster for knowledge processing tasks.

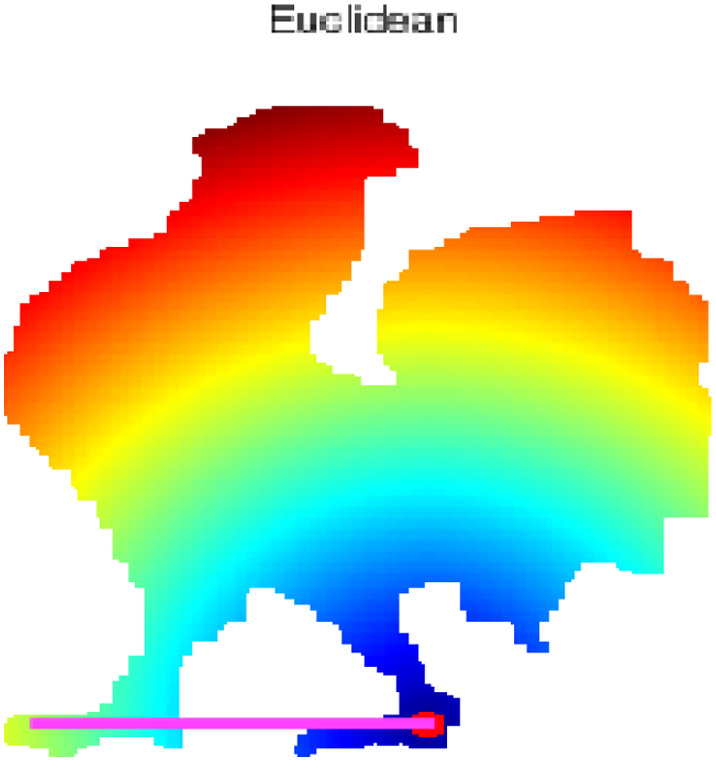Fig. 11. The difference between Euclidean and Geodesic distance

Time complexity: Let us suppose, there are n-number of non-Euclidean data sets exist in the given space. In this case, defining the function will take O(n2) time complexity among them. The characterization of those data sets in NeutroGeometry will take maximum O(n3) time complexity. In this way, the overall time complexity for characterization of non-Euclidean data in true, false, and uncertain regions may take maximum O(n3) time complexity. In the next section, some of the real examples for non-Euclidean geometry are discussed for various applications.

IV.DATA SETS WITH NON-EUCLIDEAN GEOMETRY AND ITS CHARACTERIZATION

Recently, some of the authors paid attention towards NeutroAlgebra and NeutroGeometry for data visualization [1,12–17]. Same time, some authors focused on dealing with these data sets using the fourth dimension [2] and Turiyam set [18]. This paper focused on dealing with the non-Euclidean data and its characterization.

Example 1.(Astronomy) [27]: The precise analysis of astronomy or positional astronomy is a branch of data with non-Euclidean geometry. It is used to locate any astronomical objects on the celestial sphere for the given date, time, and its spatial location on the Earth. The mathematical representation of astronomy and its pattern is based on spherical geometry and its algebra as shown in Fig. 12.In this way, the Superior planets may have a larger orbit when compared with inferior planets as per spherical geometry. It means the transit may occur in case the inferior planet passes through the given point of conjunction. It means the place of any object in the sky and its pattern can be found.

Example 2.(Surface growth) [28]: There are many numbers of processes which define the surface growth. It will provide growth of gravitational bodies, plants [29], nanostructures, and its phase transitions are one of the suitable examples. Even 3D printing and cell mobility are also an example of non-Euclidean geometry. All of these cases can be represented using the Riemannian geometry, i.e., time and space-dependent curvature.

Example 3.(Anisotropic filtering)[30]: In case a computer scientist wants to enhance the image quality of a given textures. This can be done via steeply angled rather than right angled with respect to the given point which required NeutroGeometry. It can be characterized as follows:

  • (i)True image (1, 0, 0): In case the true image is made via enhancing the image which can be represented as (1, 0, 0). This type of concept can be used in criminal face detection.
  • (ii)False image (0, 0, 1): The image does not provide the true image or provide distinct results can be represented as (0, 0, 1).
  • (iii)Neutroimage (t, I, f): The expert is uncertain about the image and its quality after the enhancement.

Example 4.(NeutroLaws) [1,16,17,31]: The law in any country is totally uncertain and vague. It depends on hierarchical ordering of citizens and its positional power in the given country which is non-Euclidean data rather than flat. There are several cases where the same punishment will not be given to each citizen for the same act. It can be defined as follows:

  • (i)Law (1, 0, 0): In case the given law is fully applied on the particular citizen. In this case, the government or court can be considered as unbiased.
  • (ii)Anti-Law (0, 0, 1): In this case, there is no law defined for the particular act. It used to be observed when a politician or business class people never get punishment under the same law.
  • (iii)NeutroLaw (t, i, f). In this case, the law changes based on person to person, region to region, and, religion to religion. This type of law where partial influence occur by any government or higher authority can be considered as NeutroLaw. The hidden pattern in these types of data can be analyzed using non-Euclidean geometry.

Example 5.(Neutro Gender law) [17]: It is one of the most suitable examples of Non-Euclidean geometrical data where the law differs based on the gender. It can be characterized as follows:

  • (i)Women law (1, 0, 0): Let us suppose, a woman complains that a man did sexual or mental harassment to her. In this case, the given crime can be accepted immediately without proper proof also.
  • (ii)Men Law (0, 0, 1): Let us suppose, a man wants to complain that a lady did sexual or mental harassment to him. In this case, the given crime cannot be accepted immediately with providing several proofs also.
  • (iii)NeutroLaw (t, i, f) : In case a transgender reports about sexual or mental harassment no body listen. The law differs for them which shows indeterminacy and incompleteness. In this case, the entire data can be considered as uncertain and vague.

Example 6.(Neutro Citation) [1,1–18,32]: The characterization of a citation for intellectual measurement cannot be done via flat way like Euclidean geometry. It requires non-Euclidean classification as follows:

  • (i)Citation (1, 0, 0): A paper cited by the domain expert, keyword, or methodology matching for the given topic can be considered as relevant citation (1, 0, 0).
  • (ii)Anti-Citation (0, 0, 1): A paper cited in irrelevant way, a retracted paper citation, a posthumous authors papers citation, same departmental citations beyond the relevant of topic, host conference citation without relevancy, forced citation, and random citation can be considered as Anti-Citation(0, 0, 1).
  • (iii)Neutro-Citation(t, i, f): A paper which is cited with interdisciplinary, collaboration, self-citations, influenced citations, honors citations, editorial citation, journal citations, etc. can be considered as Neutro-Citation (t, I, f).

Example 7.(Brain Drain Analysis) [33]: The brain drain and its parameter cannot be defined as Euclidean space. It happens in parallel when conflict arises with the given boss or management. In this case, many intellectuals leave the organization at the same time in a parallel way. The problem arises when many authors published the documents in a given domain. In this case, precise analysis of brain drain becomes difficult for the organization which can be characterized as follows:

  • (i)Brain Drain (1, 0, 0): In case the authors having many papers in chosen research domain with highly citation left, the organization can be considered as brain drain. This provides a pattern that the management does not care about brain drain when all the authors left the organization.
  • (ii)Anti-Brain Drain (0, 0, 1): The authors who published the paper using posthumous authors [34] papers to claim as real author of the given areas and left the organization can be considered as anti-brain drain. In the same time the authors who have not published any papers in the given domain left, the organization can be characterized as anti-brain drain (0, 0, 1). This will provide a pattern about policy of management when all the authors having no papers left the organization.
  • (iii)Neutro Brain Drain (t, i, f): This problem arises when multiple authors papers are available in the given domain. In the same time, the author publishes several research papers in different domain as interdisciplinary. In the same time, the author whose papers retracted from the given journal due to some issues. The collaborative work and non-journal publications can be considered as uncertain publications. These types of data can be categorized as Neutro Brain Drain. It needs more metric and depth analysis like work pressure, less salary, demotions, or other issues arises.
In this case, the non-Euclidean geometry may provide a new metric for brain drain and dark data analysis [35] which needs a quantum space to analyze the momentum of human cognition.

Example 8.(Quantum Space) [36]: It is mathematical transformations to understand the momentum and its measurements in space–time which can be considered as common wisdom. It can be understood using an example as you want to travel in the given (x, y) co-ordinates. In this case, the traversal criteria do not matter whether you go x steps right and then you go y steps forward and vice versa [37]. It means the non-commutative geometry cannot be represented precisely which requires fuzzy spherical co-ordinates. The reason is space and time contains fuzziness while precise representation is discussed by Heisenberg’s. It says that whenever someone tries to fix the momentum of any particle then its position becomes uncertain, and vice versa. It means the measurement of position and momentum depends on their ordering due to its non-commutative property which needs space–time connection.

Example 9.(Fuzzy Spherical or Harmonics) [38]: It provides a non-commutative geometrical representation of data using their spin. The product of spin provides distinct results to measure the position of a given harmonic. It means this geometry provides a way to characterize them in positive, negative, and uncertain regions based on orthonormal functions. Any point defined on the surface of the fuzzy sphere can be represented as spherical harmonics as shown in Fig. 13. One of the related examples is periodic or circular function represented using sines and cosines, i.e., Fourier series.

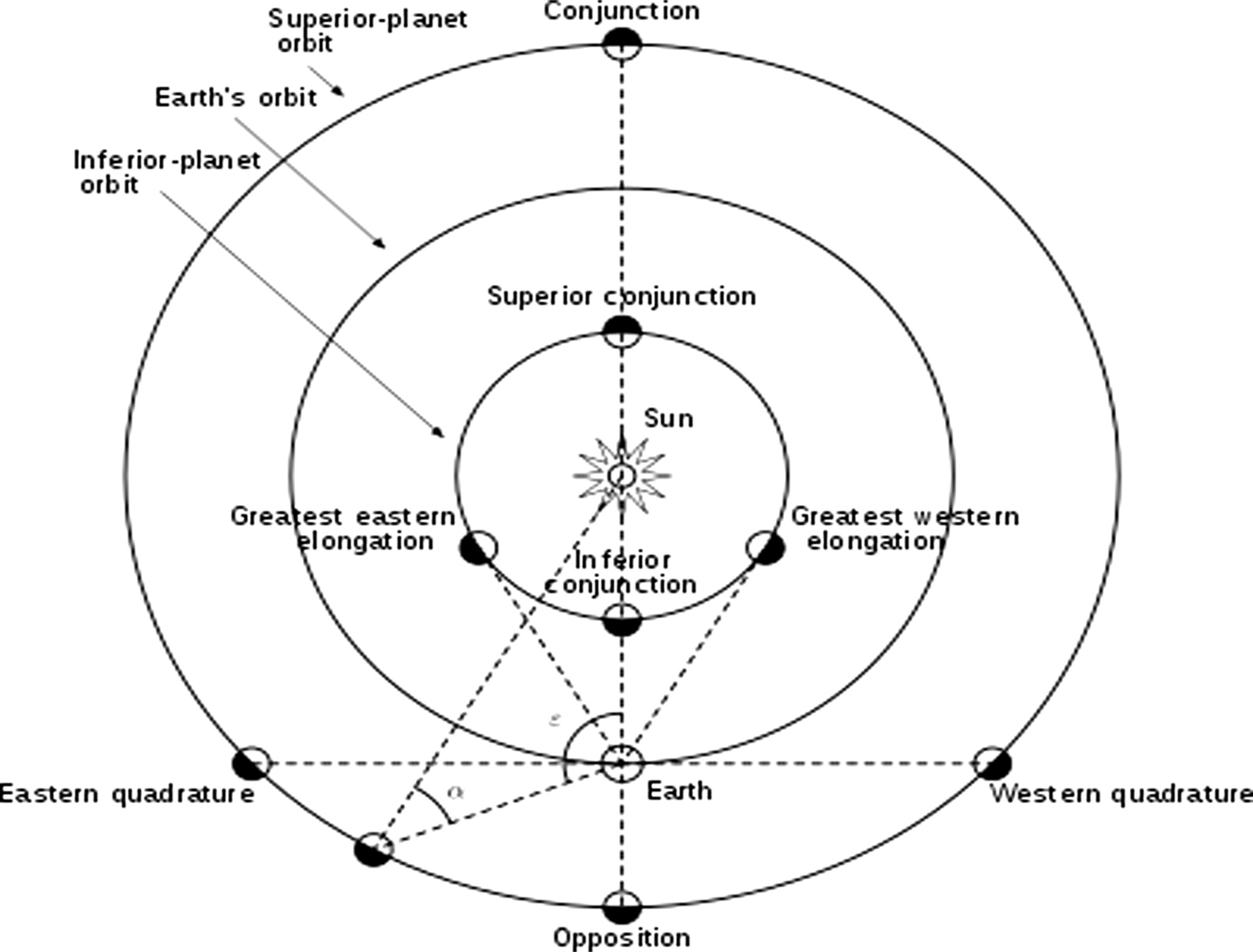Fig. 12. A non-Euclidean astronomy data and its visualization

Fig. 13. The visual representation of spherical harmonics

The current paper explores some non-Euclidean data sets and its characterization. In near future, the author will focus on introducing some new metrics to find the pattern in non-Euclidean geometrical data sets and NeutroGeometrical data sets.

V.CONCLUSIONS

This paper put forward effort towards dealing with the non-Euclidean geometry and its characterization. To achieve this goal, a method has been proposed in Section III for its analysis with its illustration in Section IV. In the future, the author will focus on introducing some new techniques to find the pattern in non-Euclidean data sets and exploring the NeutroGeometry with illustrative examples to distinguish them.