I.INTRODUCTION
Dragon and Lion Dance (DALD), as a treasure of traditional Chinese culture, carries a profound historical heritage and unique ethnic characteristics, and they are one of the important festival activities of the Chinese nation. They not only play an important role in important festivals and celebrations, such as the Spring Festival, but also serve as important symbols of Chinese cultural exchange with the outside world [1]. With the advancement of globalization and the changes in modern lifestyles, these traditional art forms face dual challenges of inheritance and development. How to protect its traditional essence while utilizing modern technological means for innovative inheritance has become an urgent problem to be solved [2,3]. In motion capture and analysis, traditional graph convolutional networks (GCNs) have made some progress in processing graph-structured data, but they have limitations in handling multimodal and heterogeneous data, especially in describing complex interaction relationships between entities. Hypergraph convolutional network (HGCN), as a new type of graph neural network, provides a more flexible and powerful framework for representing and processing complex data relationships by allowing edges to connect multiple nodes. This is particularly important for capturing complex motion interactions in DALD [4,5]. To cope with the challenges in the inheritance and teaching of DALD, an HGCN-based action evaluation method for DALD teaching is proposed. The self-attention mechanism (AM) is combined to further improve the model’s ability to capture action details. By constructing the HGCN model and combining it with data visualization techniques, the quality of DALD actions can be accurately evaluated. This model can intuitively display the evaluation results of actions, enhance user understanding and satisfaction, and open up new paths for the inheritance of intangible cultural heritage in digital sports.
Section II of this paper reviews the recent research progress of HGCN in movement assessment and digital inheritance of Sports Intangible Cultural Heritage (SICH) and analyzes its application potential in DALD teaching. Section III introduces the methods used in the research in detail, including the construction process of the action evaluation model of DALD teaching based on HGCN and the design idea of data visualization technology. Section IV shows the experimental results, evaluates the performance of the evaluation model of the DALD teaching movement based on HGCN, and analyzes the application effect of data visualization technology in the inheritance of digital SICH. Section V discusses the contributions, summarizes the results, and points out the future research direction.
II.RELATED WORK
With the rapid development of artificial intelligence and machine learning technology, the inheritance and innovation of traditional SICH are facing unprecedented opportunities and challenges. Zheng C et al. proposed a new method based on a multi-hypergraph feature aggregation network to address the challenge of modeling conversation context in session emotion recognition. This method constructed multiple hyperedges containing contextual windows, speaker information, and inter-discourse position information and used these hyperedges to aggregate local and global contextual information to improve the performance of emotion recognition. The results on the IEMOCAP and MELD datasets validated the effectiveness of this method while demonstrating lower GPU memory consumption [6]. Ping Xuan et al. constructed a long non-coding RNA (lncRNA) disease association prediction model based on adaptive hypergraphs and gated convolutions to address the identification of disease-related lncRNAs. This model integrated the biological characteristics, topological features, and gate enhancement features of lncRNA and diseases. It constructed a hyperedge to reflect the multiple relationships between lncRNA and diseases and utilized dynamic HGCN adaptive learning features to form an evolved hypergraph structure. This method outperformed seven advanced methods in terms of prediction performance, and ablation studies and case studies further validated the effectiveness and application potential of the model [7]. Faced with the challenge of dynamic simulation within and between modalities in multimodal sentiment analysis, Huang J et al. proposed the multimodal Dynamic Hypergraph Enhancement Network (DHEN). This method learned intra-modal and inter-modal dynamics through a unimodal encoder, DHEN, and HyperFusion modules. DHEN outperformed graph-based models on the CMU-MOSI and CMU-MOSEI datasets and has achieved the latest and best results on the CH-SIMS dataset, validating its effectiveness and superiority in multimodal sentiment analysis [8]. To address the limited global feature representation ability in hyperspectral image classification, Xu Q et al. proposed a concise HGCN for semi-supervised hyperspectral image classification. This method provided more stable and effective classification performance than some advanced depth methods on four real-world benchmark hyperspectral image datasets, even with very limited training samples. The overall accuracy exceeded 95% on different datasets, demonstrating its superiority in hyperspectral image classification [9].
In summary, these studies have made certain progress in action recognition and basic action analysis, providing new ideas and tools for the processing of action data. However, traditional GCNs have limited ability to describe complex multimodal and heterogeneous data in DALDs. Therefore, to achieve accurate evaluation of DALD actions and improve teaching efficiency, this study proposes a DALD-teaching action evaluation (TAE) method based on HGCN. By utilizing the advanced representation function of HGCN and combining it with self-AM, the subtle details of DALD actions can be accurately captured, achieving efficient and precise evaluation of these actions. The innovation of the research lies in the addition of self-AM in HGCN, which can grasp the interactions between various elements within the input sequence. This study focuses not only on the accuracy of action assessment but also on the inheritance of digital SICH. Through data visualization technology, the results of action evaluation are visually displayed, enhancing user understanding and satisfaction.
III.METHODS AND MATERIALS
This study first constructs a TAE model based on HGCN to process and analyze complex action data of DALD. Subsequently, this study develops a set of data visualization techniques to display and inherit this action information, making the digital inheritance of SICH more intuitive and effective.
A.DALD-TAE BASED ON HYPERGRAPH CONVOLUTION
In mathematics, a hypergraph is a generalization of a graph in which an edge can join any number of vertices. In contrast, in an ordinary graph, an edge connects exactly two vertices. HGCN plays a key role in the field of feature learning. In many real-world scenarios, the connections between entities often go beyond basic binary relationships and are difficult to capture complex interactions between data points using a single graph structure. In response to this complexity, hypergraph models have become the preferred choice due to their ability to represent more complex relationships [10,11]. The hypergraph structure is shown in Fig. 1.
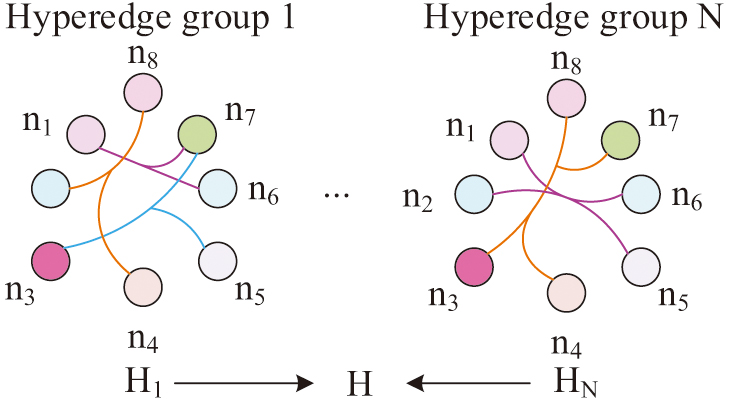 Fig. 1. Schematic diagram of hypergraph structure.
Fig. 1. Schematic diagram of hypergraph structure.
Figure 1 shows a schematic of the hypergraph structure, which includes two hyperedge groups: hyperedge group 1 and hyperedge group N. In these hypergraphs, each edge has the capacity to connect multiple nodes, in contrast to the typical graph structure in which each edge is limited to connecting only two nodes. Nodes in the diagram are represented by different colored circles, while hyperedges are represented by line segments connecting these nodes. In hyperedge group 1, nodes n1, n2, n3, etc., are connected with each other through different superedges, forming a complex relationship network. Similarly, in the hyperedge group N, nodes n1, n2, n3, etc., are also connected to each other through hyperedges. The flexibility of this structure enables the hypergraph to represent more complex relationships and is suitable for capturing complex motion interactions in DALD. The arrows H1 and HN in the graph point to the entire hypergraph structure H, respectively, representing the transformation process from a single set of hyperedges to the overall hypergraph structure. The process of hypergraph convolution is to first convert the hypergraph into a weighted regular graph and then perform graph convolution operations on the regular graph [12,13]. In HGCN, the single update operation for a certain node is shown in Fig. 2.
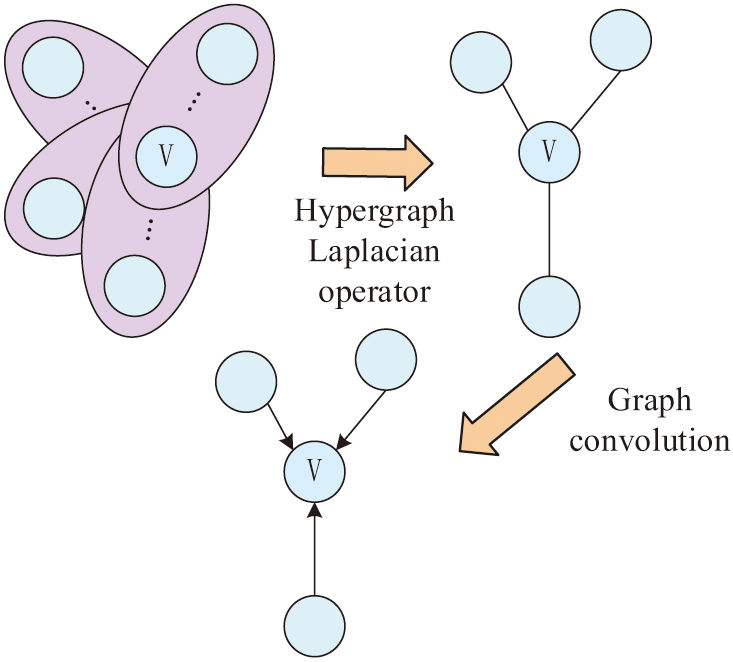 Fig. 2. HGCN update operation flow chart.
Fig. 2. HGCN update operation flow chart.
In Fig. 2, node involves five hyperedge events. In each training cycle, where all data are input into the network. Completing a complete calculation process will result in a simple edge defined by a specific element, belonging to the set of edges . In some cases, not all directly connected edges with significant features are included in the node. Therefore, only three edges are presented in the study. When performing graph convolution operations, only directly connected edges that are directly connected to nodes are included. During the training process, this process is performed on each node in the set of nodes belonging to the supernode in each cycle. This process will continue until the model reaches a stable state. HGCN can perform convolution calculations on hypergraphs to extract deeper level feature data. In scenarios involving human movements, the collaborative work of multiple joints can be described through hypergraphs to capture deep level action details that are difficult to obtain with conventional images [14,15]. Self-AM can be seen as a transformation function that can be applied to both input data and the output results of a hidden layer. The schematic diagram of AM is shown in Fig. 3.
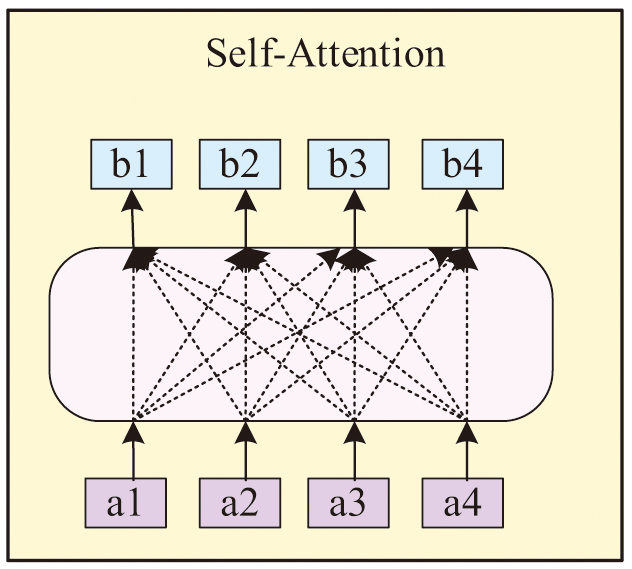 Fig. 3. Schematic diagram of the self-attention mechanism.
Fig. 3. Schematic diagram of the self-attention mechanism.
In Fig. 3, for each input vector , after self-attention processing, a new vector will be generated. The composite vector aggregates the data of all input vectors. After there are four input vectors, correspondingly, four corresponding output vectors will also be generated. AM is integrated into the HGCN architecture to construct the DALD-TAE model. The specific implementation of this mechanism in the encoder–decoder architecture is shown in equation (1):
In equation (1), is the action evaluation result at the n-th time step. is the input data for all time steps. In the DALD-TAE model, action encoding can capture the hidden layer state of the network at the final time point. By utilizing the generated sequence information and action encoding, the next action can be predicted. When making predictions, the model splits the joint probability of the target action to obtain the conditional probabilities of each action, as shown in equation (2):
In equation (2), is the probability of the entire action sequence, that is, the likelihood of observing a specific action sequence given the model parameters. In the DALD-TAE model, the weight vectors involved in AM are specifically shown in equation (3):
In equation (3), is the attention weight of the i-th hidden state at time step . is the current hidden state. is the i-th hidden state. Under the framework of the DALD-TAE model, the calculation of the target action state value is specifically shown in equation (4):
In equation (4), is the target action state value at . is the action encoding in . AM reconstructs the connections and feature matrices between nodes in the network through multiple attention heads, as shown in equation (5):
In equation (5), is the attention weight matrix of the m-th attention head. is the square root of the hidden state dimension. is the weight matrix. The integration of AM has had an impact on the processing of time series data. The processing details of each layer feature in this model are shown in equation (6):
In equation (6), is the output of the j-th attention head in the l-th layer AM. is the output of the layer before the j-th attention head. Combining AM with GCN in DALD-TAE can utilize structured information and action element features to complete the evaluation. This mechanism integrates the weights of the relationship matrix through multi-head attention, making the evaluation results more accurate and closer to the judgment of professional evaluators [16–18]. The constructed HGCN-DALD-TAE model is shown in Fig. 4.
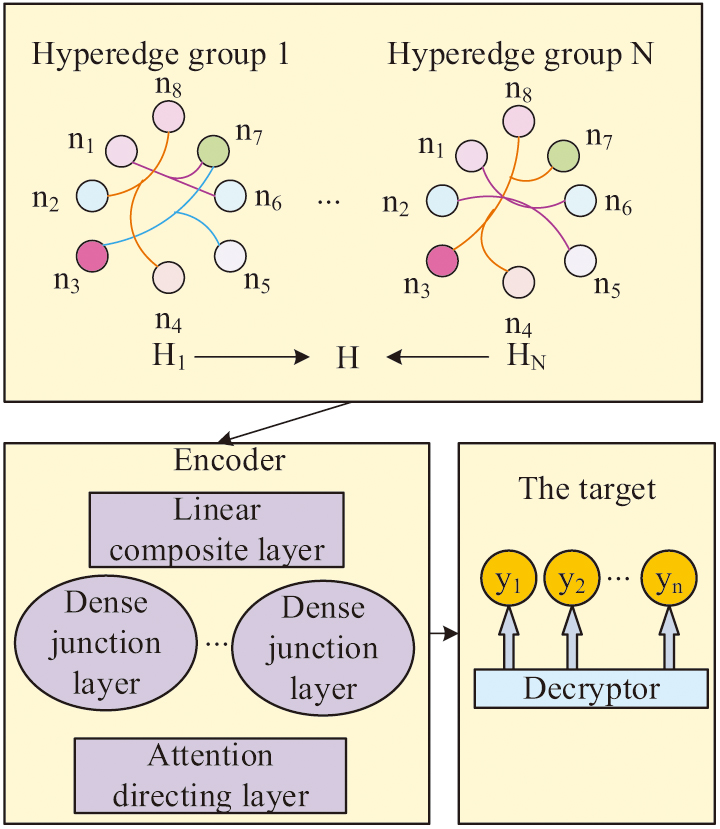 Fig. 4. HGCN-DALD-TAE model framework.
Fig. 4. HGCN-DALD-TAE model framework.
In the framework of Fig. 4, the attention guiding layer and dense connection layer replace the input layer and hidden layer of the traditional encoder. The relationship matrix and feature matrix constitute the input layer of the model. Each state of the feature matrix corresponds to a one-dimensional effective composition matrix. In this model, each action represents a node, and the connections between nodes represent the connections between actions. By analyzing these connections, the model can infer the meaning of action sequences and achieve automated TAE.
B.DIGITAL SICH INHERITANCE BASED ON DATA VISUALIZATION
This study elaborates on the DALD-TAE method based on hypergraph convolution and explores how to further promote the inheritance of digital SICH through data visualization technology. Visualization technology presents data through visual elements such as charts and graphs. This method makes the interpretation of data intuitive, allowing users to almost immediately understand the information that the data is intended to convey. Visualization not only helps to reveal patterns and trends in the data but also further explores the deep value of the data. The visualization process includes data collection, processing, mapping to visual form, and final user reception and understanding [19–22]. The process of the SICH inheritance data visualization model is shown in Fig. 5.
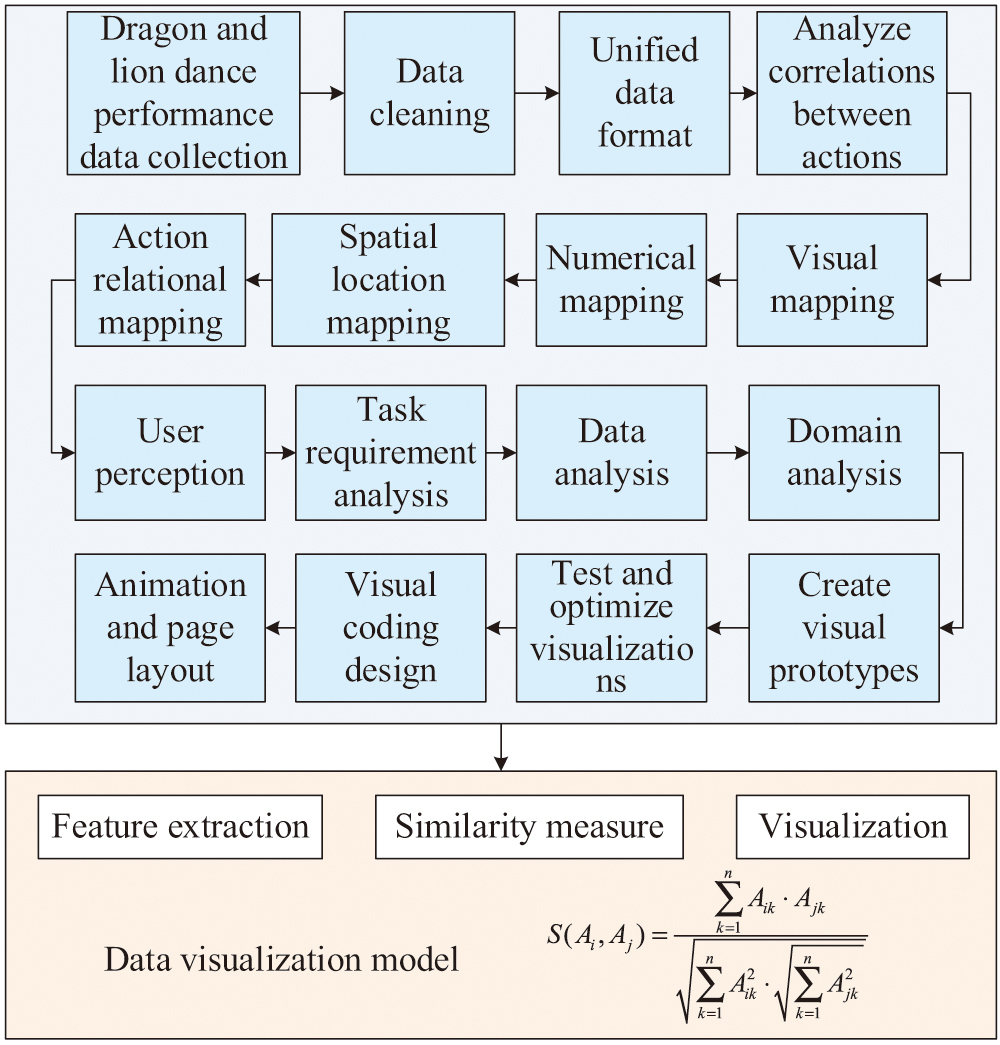 Fig. 5. Flow chart of visualization model of SICH inheritance data.
Fig. 5. Flow chart of visualization model of SICH inheritance data.
In Fig. 5, first, multi-source data of DALD performance are collected, including video, image, and sensor data. Subsequently, the data processing stage involves cleaning, formatting, and relationship analysis to ensure the accuracy and consistency of the data. In the visualization mapping phase, the relationships between data values, spatial positions, and actions are mapped to visual elements such as color, shape, and size. Through visual coding design, combined with typesetting, color theory, and animation, each dimension of data is intuitively presented. The user perception stage allows users to explore the data in depth through an interactive interface, thereby obtaining a direct perception of the quality of dance movements. The entire visualization design process includes analyzing task requirements, data characteristics, and application domains, ultimately generating a complete visualization model that integrates analysis, design, and user interaction. This is not only helpful for teaching and evaluation but also an important tool for the digital inheritance of SICH [23–25]. By using the proposed DALD action comparison analysis technique, a visual display design of relevant action information can be carried out. The visual display framework for DALD action information is shown in Fig. 6.
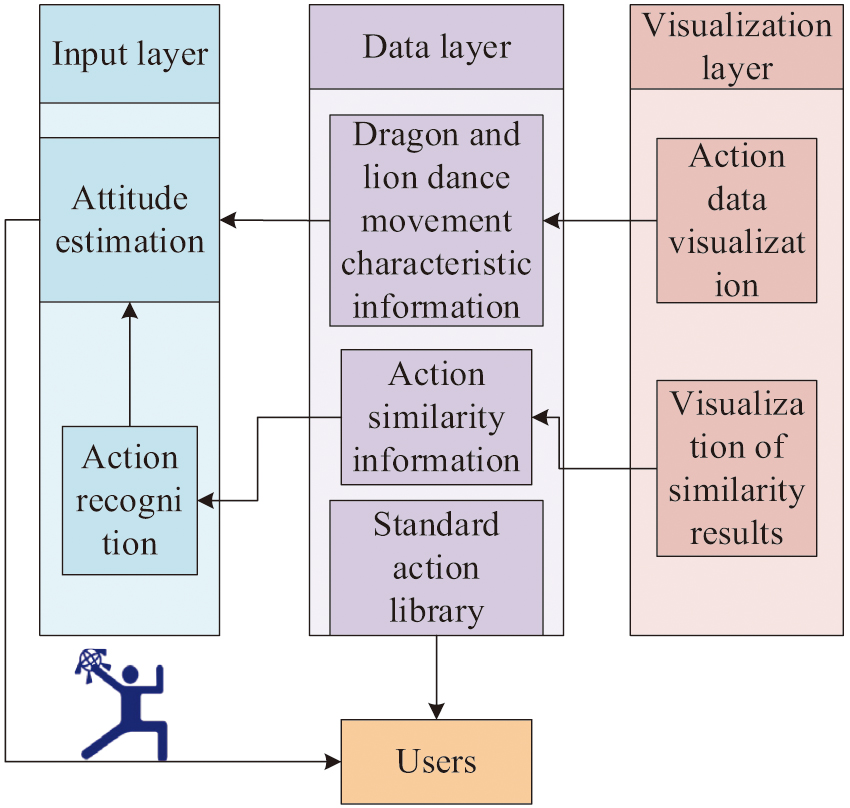 Fig. 6. The visual framework of the movement information of the DALD.
Fig. 6. The visual framework of the movement information of the DALD.
In Fig. 6, the framework consists of three main layers: the input layer, the data layer, and the visualization layer. The input layer includes two modules, action recognition and pose estimation, which are responsible for extracting action features of DALDs from raw data. The data layer is the core of the framework, consisting of three parts: DALD action feature information, action similarity information, and standard action library. The action feature information module stores specific action data for DALD. The action similarity information module is used to compare and analyze the similarity between different actions. The standard action library provides a set of standardized action templates for comparison and learning purposes. The visualization layer presents the information of the data layer to users in a graphical manner, including the visualization of action data and the visualization of similar results. The action data visualization module presents the actions of DALD in an intuitive form. The visualization of similarity results displays the comparison results between different actions.
IV.RESULTS
This study presented the performance evaluation of the DALD-TAE model based on HGCN and analyzed the application effect of data visualization technology in digital SICH inheritance. By comparing experimental data and expert evaluations, this study aimed to validate the accuracy of the model and the effectiveness of the evaluation tool.
A.EXPERIMENTAL PARAMETER SETTINGS AND PERFORMANCE EVALUATION OF HGCN ALGORITHM
The dataset of DALD movements was created specifically for the study and obtained by using a Kinect sensor for high-precision motion capture of a variety of standard DALD movements performed by professional dancers in a controlled environment. The dataset recorded in detail the joint positions and movement trajectories of the limbs of dancers performing traditional DALDs, ensuring the accuracy and detail richness of the movement data. In the collection process, multiple cameras and sensors were used to capture key body parts such as the dancer’s wrists, elbows, knees, ankles in three-dimensional coordinates, totaling 16 key points. This provided high-quality data support for DALD-TAE based on hypergraph convolution and the inheritance research of digital SICH. Table I shows the experimental parameters.
Table I. Experimental settings and parameters
| Parameter | Configuration value | Parameter | Configuration value |
|---|---|---|---|
| CPU | Intel Core i7-9700K @ 3.6GHz | Network architecture | TC-HGCN |
| GPU | NVIDIA GeForce RTX 2080Ti | Number of floors | 10 |
| RAM | 32GB DDR4 3200MHz | Channel width | 64, 64, 64, 64, 128, 128, 128, 128, 256, 256, 256 |
| Store | 1TB SSD | Learning rate | 0.1 |
| Operating system | Windows 10 Professional 64-bit | Attenuation factor | 0.1 |
| Development environment | PyTorch 1.7.1, CUDA 10.2 | Batch size | 64 |
| Dataset | NTU RGB+D 60 & 120 | Training epoch | 65 |
| Warm-up strategy | The first five ages | Optimizer | SGD with Nesterov momentum 0.9, weight attenuation 0.0004 |
In Table I, the hardware configuration included Intel Core i7-9700K CPU, NVIDIA GeForce RTX 2080Ti GPU, 32GB DDR4 memory, and 1TB SSD storage. The software environment was Windows 10 Professional 64-bit operating system, and the development tools were PyTorch 1.7.1 and CUDA 10.2. The model architecture adopted TC-HGCN, which included 10 layers of networks, with channel widths ranging from 64 to 256 for each layer. The training process used SGD optimizer with an initial learning rate of 0.1 and decays in stages 35 and 55. The batch size was set to 64, and the total number of training cycles was 65 epochs, while implementing the warm-up strategy for the first 5 epochs. First, this study evaluated the performance of the HGCN-Attention algorithm incorporating AM and compared it with HGCN, Spatiotemporal GCN (ST-GCN), GCN, and Dynamic GCN. The accuracy, recall, and F1 values of several algorithms are shown in Fig. 7.
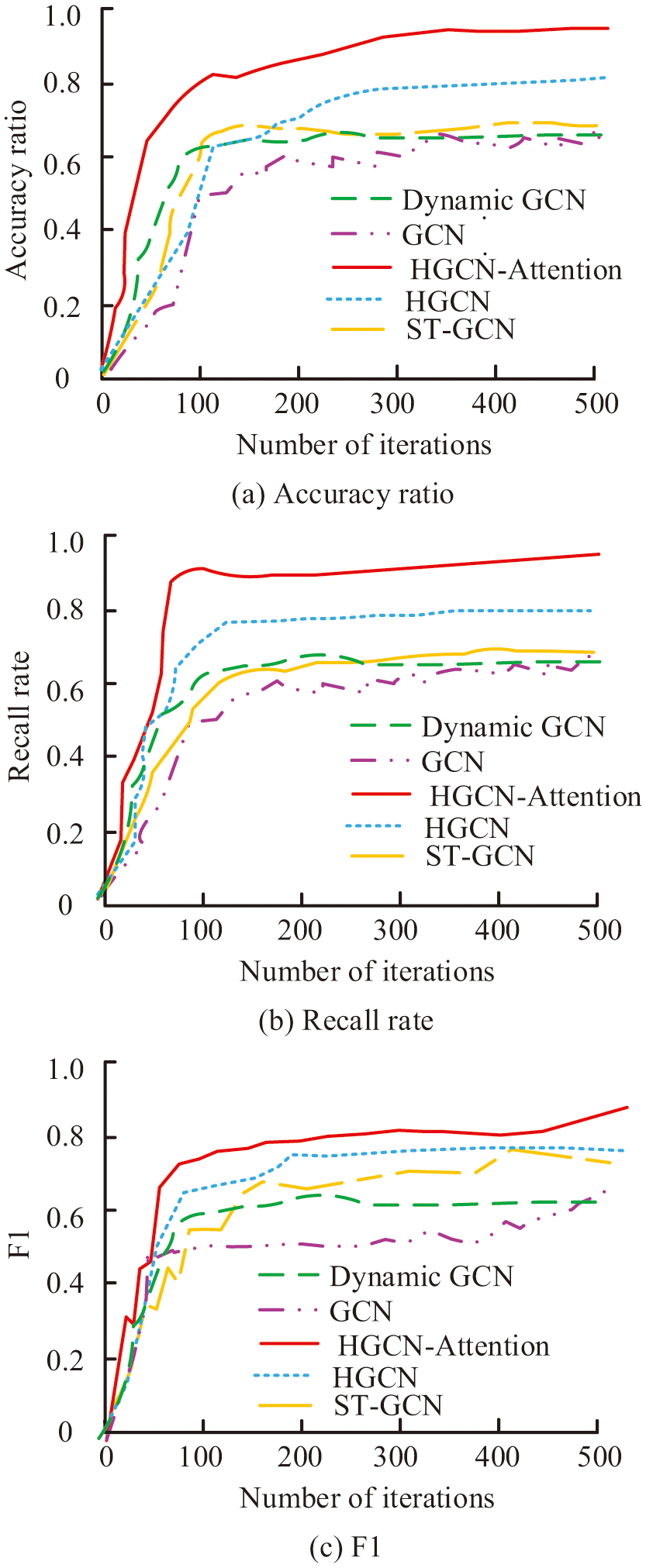 Fig. 7. Accuracy, recall rate, and F1 value of several algorithms.
Fig. 7. Accuracy, recall rate, and F1 value of several algorithms.
In Fig. 7(a), the accuracy of HGCN-Attention rapidly improved with the increase of iteration times and tended to stabilize after about 100 iterations, ultimately reaching a high accuracy close to 1.0, which is significantly better than other algorithms. In Fig. 7(b), HGCN-Attention also demonstrated excellent performance in terms of recall, quickly approaching 1.0 after 100 iterations and maintaining stability in subsequent iterations. In Fig. 7(c), HGCN-Attention also performed well in F1 value, quickly reaching above 0.8 after 100 iterations and maintaining stability in subsequent iterations, demonstrating a good balance between accuracy and recall. HGCN-Attention performed well in accuracy, recall, and F1 value, demonstrating its efficiency and superiority in processing graph-structured data. This was mainly due to the introduction of AM, which allowed the model to focus more on key information, thereby rapidly improving performance during the iteration process and ultimately achieving optimal results. The convergence of loss functions for several algorithms is shown in Fig. 8.
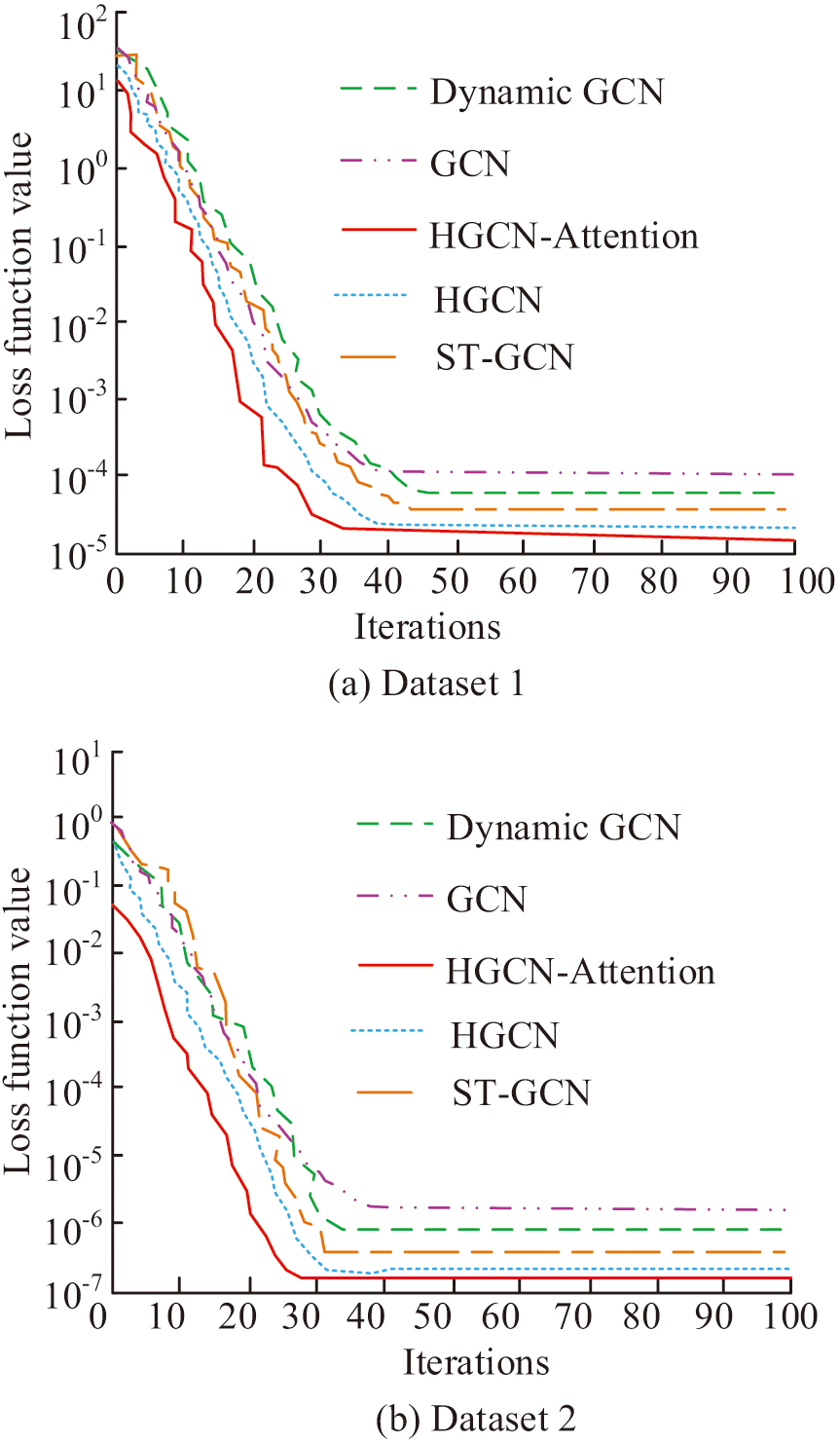 Fig. 8. Convergence of loss functions of several algorithms.
Fig. 8. Convergence of loss functions of several algorithms.
In Fig. 8(a), the loss function value of HGCN-Attention decreased the fastest and quickly stabilized after about 20 iterations, ultimately reaching the lowest loss value, indicating its best convergence speed and performance on this dataset. HGCN-Attention had better learning ability and generalization performance when processing Dataset 1. In Fig. 8(b), HGCN-Attention also exhibited the fastest convergence speed, with a rapid decrease in loss value and a tendency toward stability after 20 iterations, and ultimately the lowest loss value. On Dataset 2, HGCN-Attention still maintained its superior performance, effectively learning and generalizing to new datasets. HGCN-Attention outperformed other algorithms in terms of the convergence speed of the loss function and the final loss value, reflecting its stability and efficiency on different datasets. The introduction of AM significantly improved the performance of HGCN, enabling it to better capture key information in the feature learning process, thereby rapidly reducing losses and achieving better performance in the iterative process. The root mean square error (RMSE) and mean absolute error (MAE) of several algorithms are shown in Fig. 9.
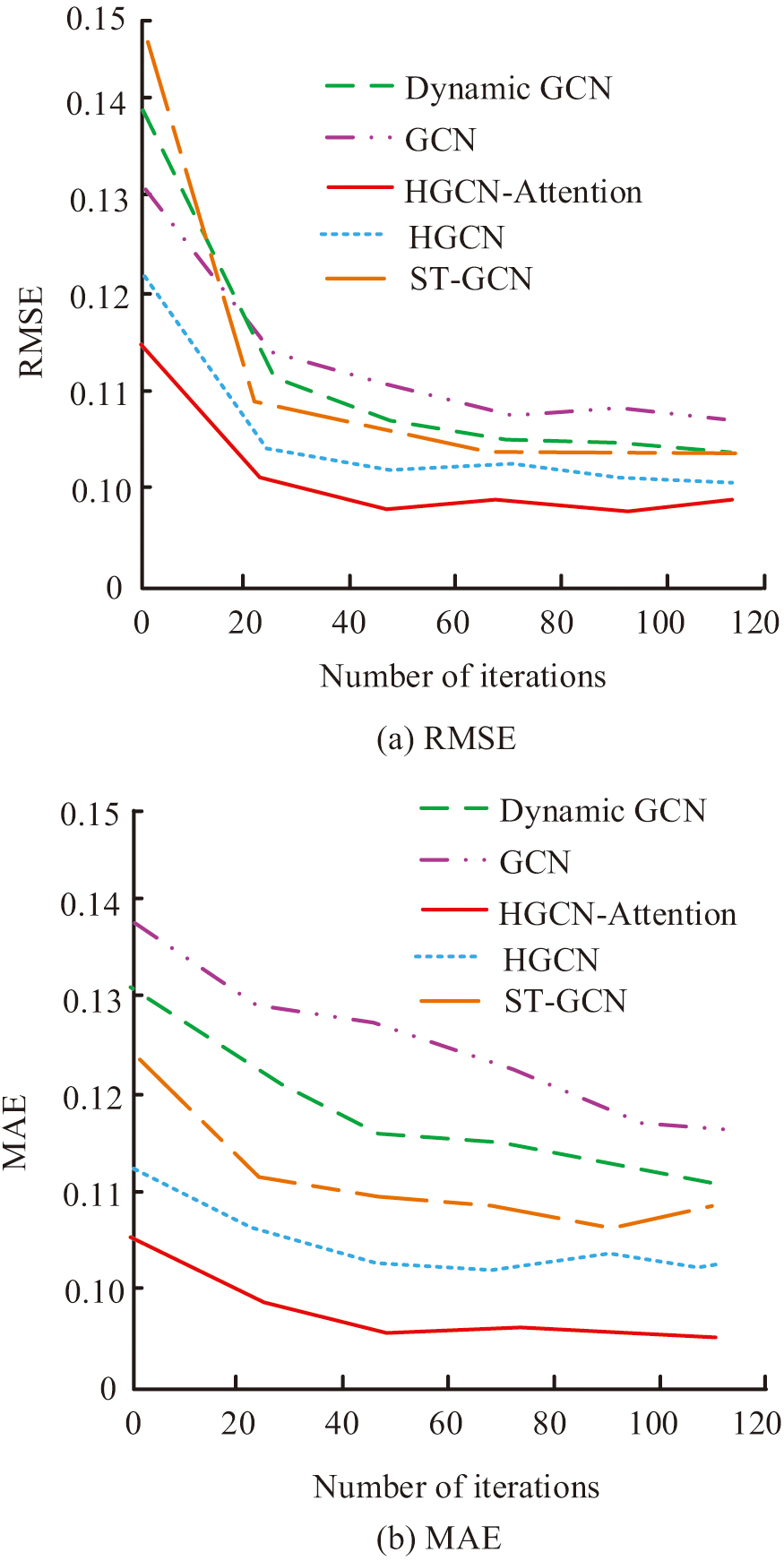 Fig. 9. RMSE and MAE of several algorithms.
Fig. 9. RMSE and MAE of several algorithms.
In Fig. 9(a), the RMSE value of HGCN-Attention rapidly decreased in the initial stage and stabilized after approximately 20 iterations, ultimately reaching the lowest RMSE value, demonstrating its superiority in error control. In Fig. 9(b), the MAE value of HGCN-Attention rapidly decreased in the initial stage and stabilized at the lowest level after approximately 20 iterations, further confirming its effectiveness in reducing prediction errors. HGCN-Attention performed the best in both RMSE and MAE key performance indicators, reflecting the important role of AM in improving model learning efficiency and prediction accuracy. The introduction of the HGCN-Attention algorithm significantly improved the model’s ability to capture key information, thereby rapidly reducing errors and achieving better performance during the iteration process.
B.DALD-TAE AND VISUALIZATION EFFECT ANALYSIS
This study applied several algorithms to DALD-TAE separately. The accuracy and evaluation time results of several algorithms during DALD-TAE are shown in Fig. 10.
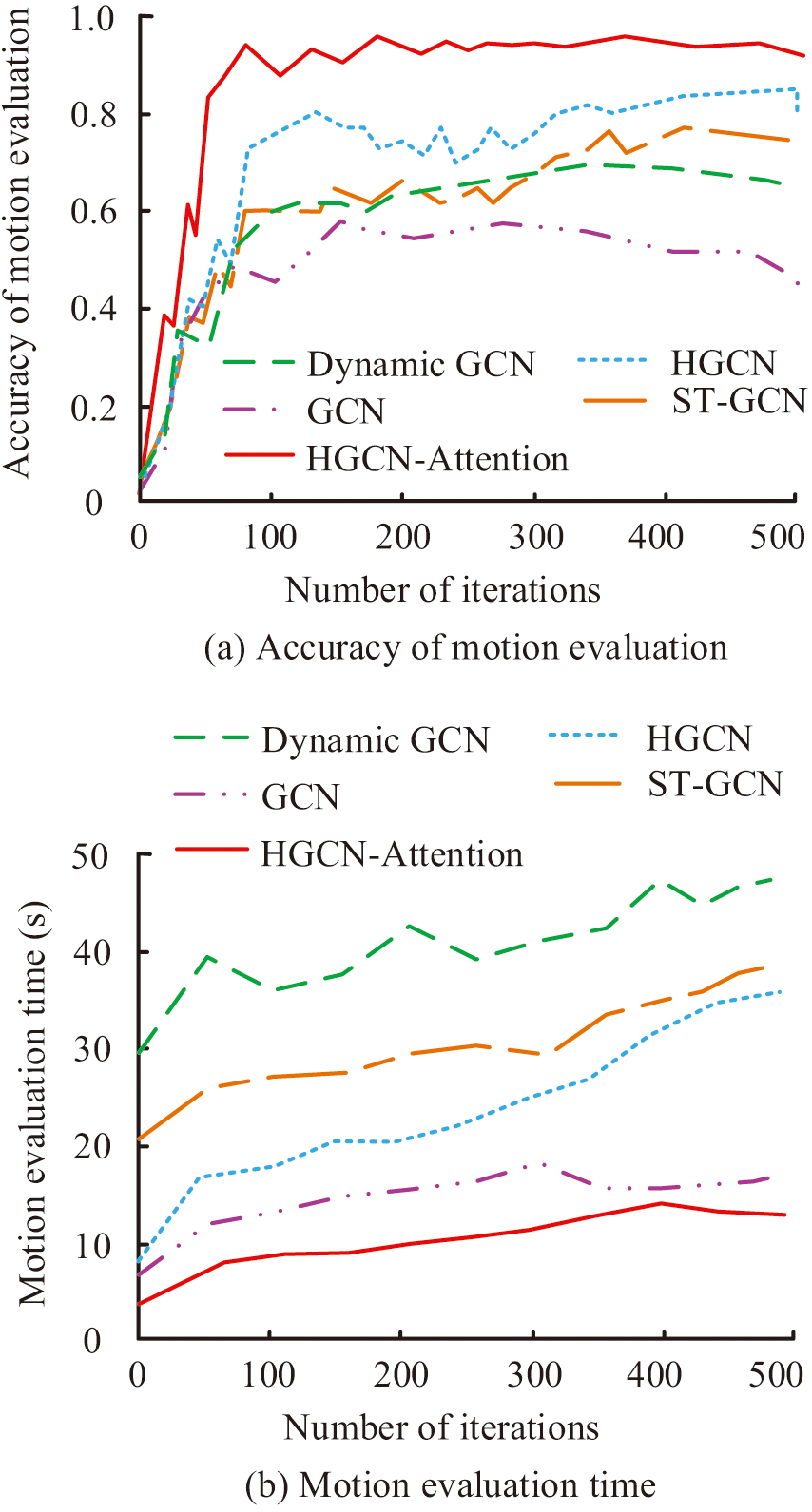 Fig. 10. Accuracy and evaluation time of teaching movement evaluation of DALD.
Fig. 10. Accuracy and evaluation time of teaching movement evaluation of DALD.
In Fig. 10(a), HGCN-Attention rapidly increased in the initial stage and stabilized after approximately 100 iterations, ultimately reaching the highest accuracy, close to 1.0. The accuracy growth of Dynamic GCN, ST-GCN, GCN, and HGCN was relatively slow, and they did not reach the level of HGCN-Attention throughout the entire iteration process. This indicated that HGCN-Attention had significant advantages in capturing DALD action features, enabling faster learning and accurate evaluation of action quality. In Fig. 10(b), the evaluation time growth of HGCN-Attention was the slowest, showing a lower evaluation time at the beginning of the iteration. Moreover, as the number of iterations increased, the growth rate was relatively small and ultimately remained at a low level. In contrast, the evaluation time of Dynamic GCN and ST-GCN increased rapidly, especially after more than 200 iterations, and the evaluation time significantly increased. Although the evaluation time of GCN and HGCN has also increased, their overall appreciation was lower than that of Dynamic GCN and ST-GCN. This indicated that HGCN-Attention not only performed excellently in evaluation accuracy but also had significant advantages in evaluation efficiency, enabling action evaluation to be completed at a lower time cost. Finally, the visualization results of the designed DALD action information were evaluated and compared with the expert evaluation results. Comparative indicators included evaluation accuracy, error rate, omission rate, evaluation efficiency, and user satisfaction. Table II shows the results of normalizing the comparison indicators.
Table II. Comparison of information evaluation of DALD movements
| Evaluation index | Expert evaluation | Visual evaluation | Percentage improvement |
|---|---|---|---|
| Evaluation accuracy | 0.682 | 0.941 | +38.06% |
| Error rate | 0.800 | 0.333 | –58.25% |
| Omission rate | 0.400 | 0.118 | –70.50% |
| Evaluation efficiency | 0.100 | 0.500 | +400.00% |
| User satisfaction | 0.800 | 0.900 | +12.50% |
In Table II, the accuracy of visual evaluation reached 0.941, a significant improvement compared to the expert evaluation of 0.682, indicating that visualization technology can more accurately capture and analyze motion features. The error rate and omission rate decreased from 0.800 to 0.333 and from 0.400 to 0.118, demonstrating the advantage of visualization methods in reducing evaluation errors and omissions. The increase in evaluation efficiency from 0.100 to 0.500 indicated that visualization technology could significantly save evaluation time and improve the efficiency of the evaluation process. User satisfaction has also increased from 0.800 to 0.900, reflecting a high level of satisfaction among users with the visual evaluation results. The DALD action information visualization method designed had significant advantages in improving evaluation quality, reducing error rates, enhancing evaluation efficiency, and increasing user satisfaction. These advantages made visualization methods of great value in the inheritance and teaching application of digital SICH, especially in situations where rapid and accurate assessment of action quality was required.
V.CONCLUSION
This study aimed to achieve precise capture and evaluation of action details by constructing a DALD-TAE model based on HGCN, thereby promoting the inheritance of digital SICH. This study used a hypergraph model to represent complex action relationships and integrated it with AM to enhance the model’s ability to learn internal relationships within action sequences. In the experiment, the HGCN-Attention algorithm outperformed traditional algorithms in multiple performance metrics. After 100 iterations, the accuracy remained stable at 0.985, the recall was 0.978, and the F1 value reached 0.982. Compared to traditional methods, the evaluation time was shortened by about 30%. The accuracy of DALD action information visualization evaluation reached 0.941, with error and omission rates of 0.333 and 0.118, respectively, showing significant advantages. These results not only validated the superiority of HGCN-Attention in action assessment but also indicated its potential in digital inheritance SICH. However, the computational complexity of the model was high, and there might be certain limitations for application scenarios that would require extremely high real-time performance. Future work will focus on optimizing the model structure, reducing computational costs, and enhancing the practicality of the model.