I.INTRODUCTION
As a treasure of Chinese traditional culture, national music (NM) carries rich historical and cultural connotations. It is essential to preserve national culture and fostering a sense of patriotism [1]. The need for impartial and precise NM performance evaluation instruments in the areas of music education (ME), cultural preservation, and creative production has grown more pressing as a result of the quick advancement of science and technology [2]. However, the traditional NM performance evaluation method mainly relies on the subjective judgment of professional musicians and lacks uniform and objective quantitative standards. The popularization and promotion of NM are severely constrained by the difficulty of meeting the standards of contemporary society for scientific and systematic music appraisal [3]. Deep learning technology has advanced significantly in the realm of music analysis in recent years, offering fresh concepts and approaches for assessing NM performances. However, there are still many shortcomings in the existing research. On the one hand, most studies focus only on the extraction of low-level features of music signals, such as pitch and rhythm, while ignoring high-level features such as style and emotion of music. This can lead to less comprehensive and accurate evaluation results. On the other hand, the ability to capture the unique micro-detail features such as ornamentation and glissando in NM performance is limited. The flavor and qualities of NM are hard to completely convey [4,5]. Specifically, while existing deep learning-based evaluation methods have made progress, they still face critical limitations. In FE, the focus remains on general music features. The systematic integration of complex spectral processing in the domain of music theory to guide feature learning has not yet been achieved. This results in difficulties in simultaneously capturing both acoustic low-level features (pitch, rhythm) and high-level musical structural features (melody, harmony, style). Although long short-term memory (LSTM) and its variants can process temporal information in temporal modeling, they generally lack attention mechanisms (AMs) to explicitly optimize feature weight distribution. Consequently, the ability to perceive temporal variations in dynamic pitch and rhythm during improvisation, as well as the elastic temporal structures characteristic of ethnic music, remains insufficient. There is a lack of quantitative frameworks that tightly integrate music theory rules. This leads to assessment results that fall short of the level of professional human auditory judgment regarding musical harmony.
Therefore, the study innovatively proposes a method for evaluating NM performance that integrates AMs and music theory rules. The method innovatively processes music audio signals by complex number convolutional neural network (CN-CNN) to extract spectral features. The LSTM algorithm is then optimized by introducing an AM to enhance the audio feature extraction (FE) capability. At the same time, the pitch, rhythm, melody, and harmony of the music performance are comprehensively analyzed in conjunction with the rules of music theory, thus realizing the automatic evaluation of the music performance.
The rest of the paper is organized as follows.
Section II: Related Work reviews the existing research in the fields of music recognition, evaluation, and the application of deep learning techniques such as CNN and LSTM in music analysis. It summarizes the progress made by previous studies and highlights the limitations that the current research aims to overcome. Section III: Methods and Materials elaborates on the construction and optimization of the NM performance evaluation model. First, it introduces the NM performance evaluation model, which is based on music theory rules and a CN-CNN. This model integrates music theory knowledge and explains the structure and working principle of the CNN. It also describes the evaluation process. Then, it explains the improved optimization of the model by incorporating the AM into the LSTM algorithm, as well as the audio preprocessing process and the overall structure of the integrated evaluation model. Section IV: Results presents the performance testing and practical application results of the proposed model. It includes the training loss curve, convergence performance, and ablation experiment results to verify the model’s training efficiency and performance improvement. Additionally, it demonstrates the model’s performance in practical applications, such as melody recognition, harmonic evaluation, and music genre classification. It also shows the model’s ability to generalize on different ethnic music datasets. Section V: Conclusion summarizes the main contributions of this study, including the development of an integrated evaluation model that addresses the limitations of traditional methods, and its excellent performance in experiments and practical applications. It also discusses the social significance and potential applications of the research, as well as the limitations of the current study and directions for future research.
II.RELATED WORK
The significance of music performance evaluation is not only limited to the technical or artistic judgment of music performance but also a comprehensive expression of cultural heritage (CH), artistic innovation, and social value. To increase the precision and effectiveness of music retrieval, Shi J et al. suggested an autonomous music annotation technique based on labeled conditional random fields. It also combined the spectrogram, Meier frequency cepstrum coefficient, and AM to construct a deep neural network model. Experiments indicated that in music hierarchical sequence modeling, all the indicators were better than the comparison algorithm, and the retrieval speed was improved by more than 30% [6]. Haoa J. et al. addressed the problems of homogenization of ME and cultural inheritance of NM and constructed a two-way empowerment system of “Teaching music in higher education-NM culture” through virtual reality teaching scenarios, artificial intelligence (AI)-assisted creation, and blockchain authentication system. The experiment revealed that students’ scores on the dimension of “sense of cultural belonging” to NM improved most significantly. The accuracy of the use of NM elements (e.g., glissando, ornamentation) increased by 34.7% [7]. Wang H et al. developed DiffuSeRoll, a diffusion-based multi-track, multi-attribute music generation system. This innovative approach enabled simultaneous creation of multiple instrumental tracks while allowing precise control over musical parameters including tempo, tonality, and emotional expression. Experimental results demonstrated that DiffuSeRoll delivered exceptional diversity and quality in multi-track music production. The generated compositions excelled in chord consistency, melodic coherence, and rhythmic complexity. They effectively met diverse creative requirements in various musical contexts [8]. Wang L et al. systematically analyzed the technological progress, East-West differences, and future directions in the field of AI music generation. The conclusion indicated that Chinese folk music emphasizes more on differential tones, complex rhythms, and cultural contexts. This required more pitch sensitivity and rhythmic understanding of AI models. Aiming at the characteristics of oriental music, this study provided theoretical support for the automated inheritance of non-heritage music, such as Xi’an drum music, which helped to lower the threshold of creation and expand the cultural influence [9].
CNN is a feed-forward neural network that performs well in complex FE. To overcome CNN’s sluggish inference speed, Xie X et al. suggested a region-oriented network model. The findings revealed that the suggested model successfully increased the accuracy and speed of inference [10]. A CNN-LSTM hybrid prediction model was presented by Zhang X et al. to address the issue of complicated seismic response data from high-speed railroads. The results indicated that the proposed model could be effectively used for seismic response analysis of railroad infrastructure [11]. To increase the effectiveness of automatic categorization of ECG signals, Ozaltin O. et al. presented a CNN model for classification. The outcomes demonstrated that the suggested methodology could be applied successfully to automatically classify ECG signals [12]. LSTM has wide applicability as it can effectively handle and predict long-term dependencies in the time-series data. Mirza F K et al. proposed a model based on residual LSTM neural network for recognizing time-dependent continuous pitch strings in Turkish classical music from spectrograms. According to the experimental findings, the model’s accuracy across all 15 seed sets was 89.09% [13]. A Xi’an drum music production technique based on bidirectional LSTM with deep reinforcement learning was presented by Li P et al. The method realized the innovative inheritance of Xi’an drum music through automated generation technology, which not only preserved its traditional musical characteristics but also reduced the threshold of creation. According to the trial results, it enhanced tuning accuracy by 18.6% and chord progression rationality by 21.4% when compared to the conventional technique. It scored higher in musical innovativeness and increased the generation efficiency by more than 50% [14]. Kasif et al. proposed a LSTM model based on hierarchical multi-head attention. This model addressed the issue that traditional symbolic music generation struggled to capture complex relationships between voices and tended to repeat local patterns while lacking global coherence. Experimental results indicated that the phrase repetition rate was reduced by 31.2% when the model generated music. The average length of the generated music was extended from 16 bars to 28 bars, and the structural coherence was significantly improved [15].
In summary, existing research has made some progress in music recognition and evaluation, but there are still problems such as lack of comprehensiveness and insufficient intelligence in its FE and intelligent evaluation. Therefore, the study proposes an intelligent evaluation model that integrates music theory rules and CN-CNN and introduces an AM to efficiently recognize and extract features of NM for evaluation. The study aims to provide a more scientific, objective, and comprehensive approach to evaluating NM performances. Additionally, it seeks to advance the intelligent and digital advancement of NM’s artistic production, CH, and education.
III.METHODS AND MATERIALS
A.CONSTRUCTION OF NM PERFORMANCE EVALUATION MODEL BASED ON MUSIC THEORY RULES AND CN-CNN
The appraisal of NM’s performances is crucial to ME, cultural transmission, and artistic advancement since it is a significant component of traditional Chinese culture. Traditional NM performance evaluation mainly relies on the subjective judgment of professional musicians and lacks objective and accurate evaluation standards and methods. Therefore, the study constructs a NM performance evaluation model based on music theory rules. A model that can objectively and accurately evaluate the quality of NM performance is constructed through the combination of music theory rules and deep learning. The basic music theory knowledge covers the core elements of pitch, rhythm, beat, melody, harmony, music notation, terminology, and so on [16]. The twelve equal temperament of pitch and the musical chart are shown in Fig. 1.
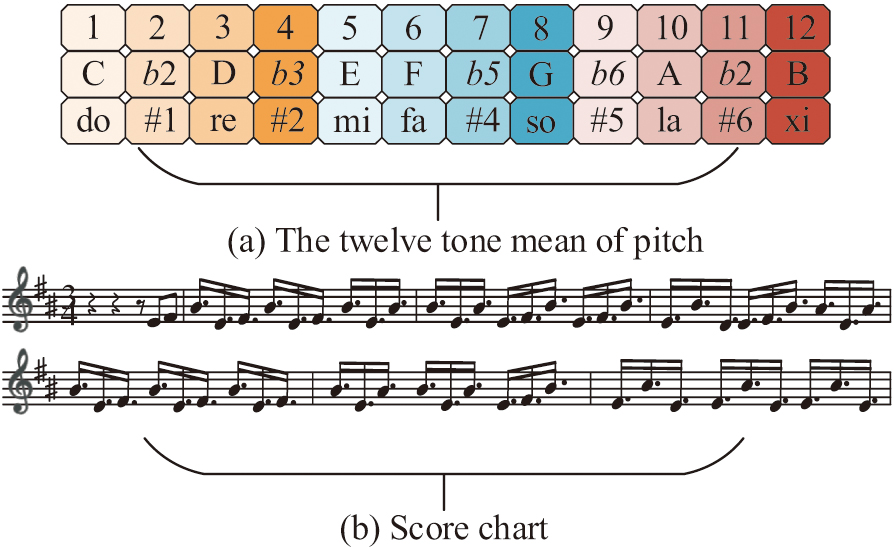 Fig. 1. The 12-tone equal temperament and musical score (Source from: Author’s own drawing) CN-CNN (Source from: Author’s own drawing).
Fig. 1. The 12-tone equal temperament and musical score (Source from: Author’s own drawing) CN-CNN (Source from: Author’s own drawing).
In Fig. 1, pitch is based on the twelve equal temperament laws and consists of whole tones and half tones. Sheet music is the earliest recorded representation of music, and the most common and basic form is the pentatonic score. On this basis, Chinese folk music theory has developed a unique system. It is based on the five tones of Gong, Shang, Jue, Zhi, and Yu and emphasizes the changes of “rhythm,” such as glissando, vibrato, and other decorative techniques. It utilizes special modes such as yanyue and qingshang, forming an elastic structure of “scattered-slow-medium-fast-scattered.” Pitch entropy is the entropy value of the pitch sequence of notes in a section of a track, as shown in equation (1):
In equation (1), denotes pitch entropy. denotes the pitch variety recognized by chord . Equation (2) illustrates the calculation of the rhythmic change stability:
In equation (2), denotes rhythmic variation stability. denotes the number of beats. ) denotes the rhythmic pattern at the time point from to . denotes the inconsistent unit in the rhythmic pattern. denotes an active unit in the rhythmic pattern. Equation (3) displays the equation for chord coherence:
In equation (3), is the coherence of the chord. is the 2nd element in the th categorization matrix in the recognition sequence. The chord regularity is shown in equation (4):
In equation (4), denotes chord regularity. denotes the 2nd classification result in the th classification. denotes chord change probability. To better capture low-level spectral features, such as pitch and rhythm, as well as high-level timbral nuances, the study combines the CN-CNN model with music theory rules. Unlike real-valued CNNs, which only process magnitude information, the CN-CNN model converts audio into a complex form via Fourier transformation, preserving the critical phase relationships that are essential for characterizing ethnic music ornamentations. This enables joint modeling of time-domain transients and frequency-domain structures. Then the audio data are dimensionalized to visualize the recognition and evaluation process [17,18]. The structure of CN-CNN is shown in Fig. 2.
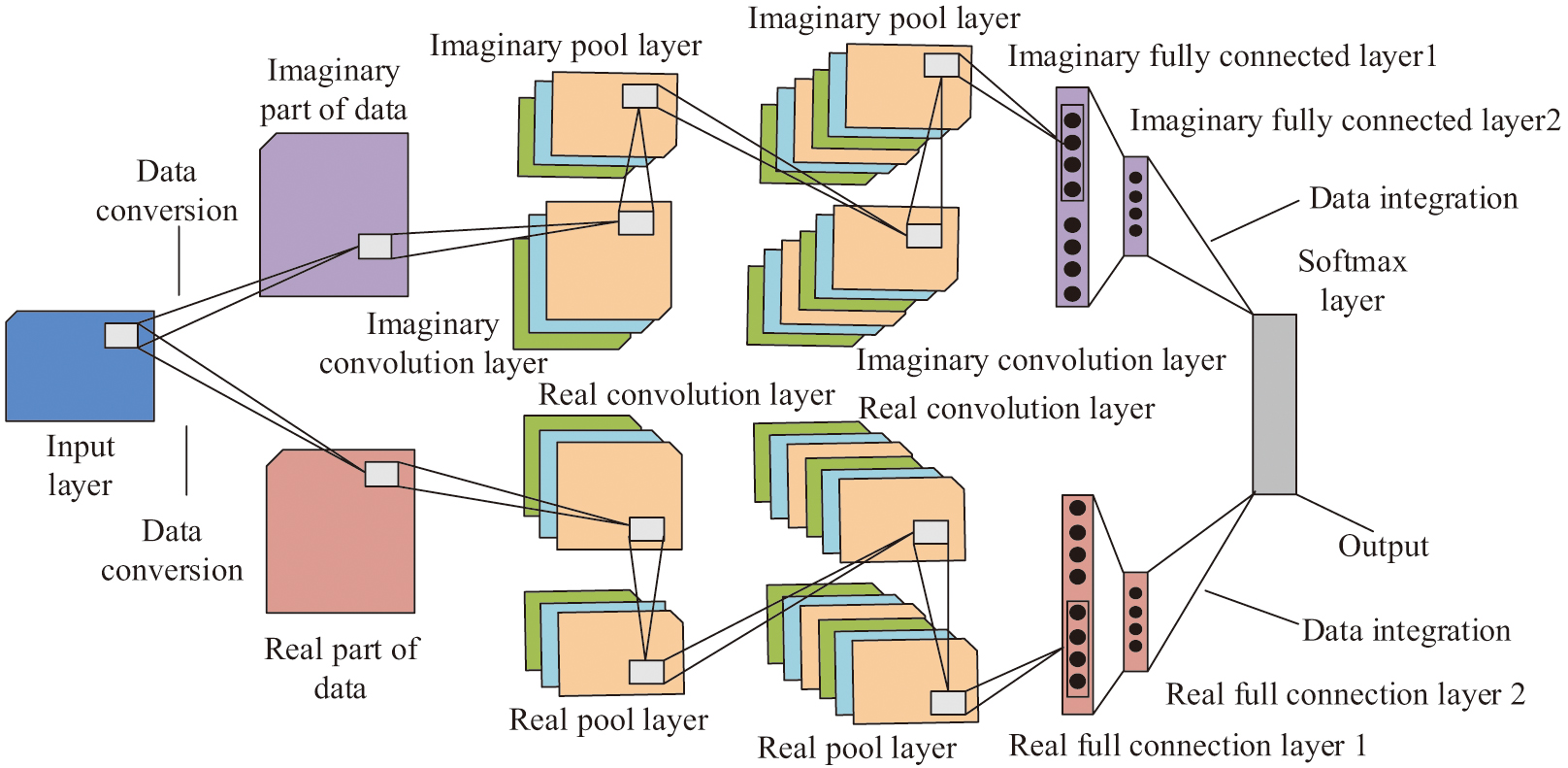 Fig. 2. CN-CNN (Source from: Author’s own drawing).
Fig. 2. CN-CNN (Source from: Author’s own drawing).
In Fig. 2, CN-CNN is an extended version of real CNN. Its architecture is the same as that of real CNN, the difference is that the input layer of CN-CNN converts the acquired music and audio signal data into complex form. It also sends its real and imaginary parts to the convolutional layer, pooling layer (PL), and fully connected layer (FCL), respectively. Before the data is passed to the output layer, this data is recombined into real number form. The complex convolution operation extends real convolution to the complex domain enabling three key advantages over real-valued CNNs: phase sensitivity which can accurately models micro-temporal variations (e.g., 0.1s glissando in Pipa), spectral completeness can represent harmonic energy and phase coherence simultaneously, and filter orthogonality real and imaginary kernel functions can learn complementary features. Its execution is done with the help of real number convolution operation [19,20]. When the complex input data (ID) is placed in a complex convolution matrix, the complex convolution calculation is shown in equation (5):
In equation (5), and are real vectors in a one-dimensional complex convolution operation. is the complex convolution kernel, which consists of two real components. is the complex input signal. is the real part of the input signal. is the imaginary part of the input signal. is the convolution operation. Maximum pooling preserves the maximum local features in the signal feature map (FM). Therefore, maximum value pooling is used in the study [21]. The maximum value pooling calculation is shown in equation (6):
In equation (6), is the output value of the th neuron of the th FM of the layer after the PL. is the output value of the th neuron of the th FM of the layer after the activation function. The complex convolutional network propagation computation process is shown in equation (7):
In equation (7), is the learning rate. is the result of the th iteration of the th layer weights. is the loss function. is the th layer bias th iteration result. The flow of NM performance evaluation based on music theory rules and CN-CNN is shown in Fig. 3.
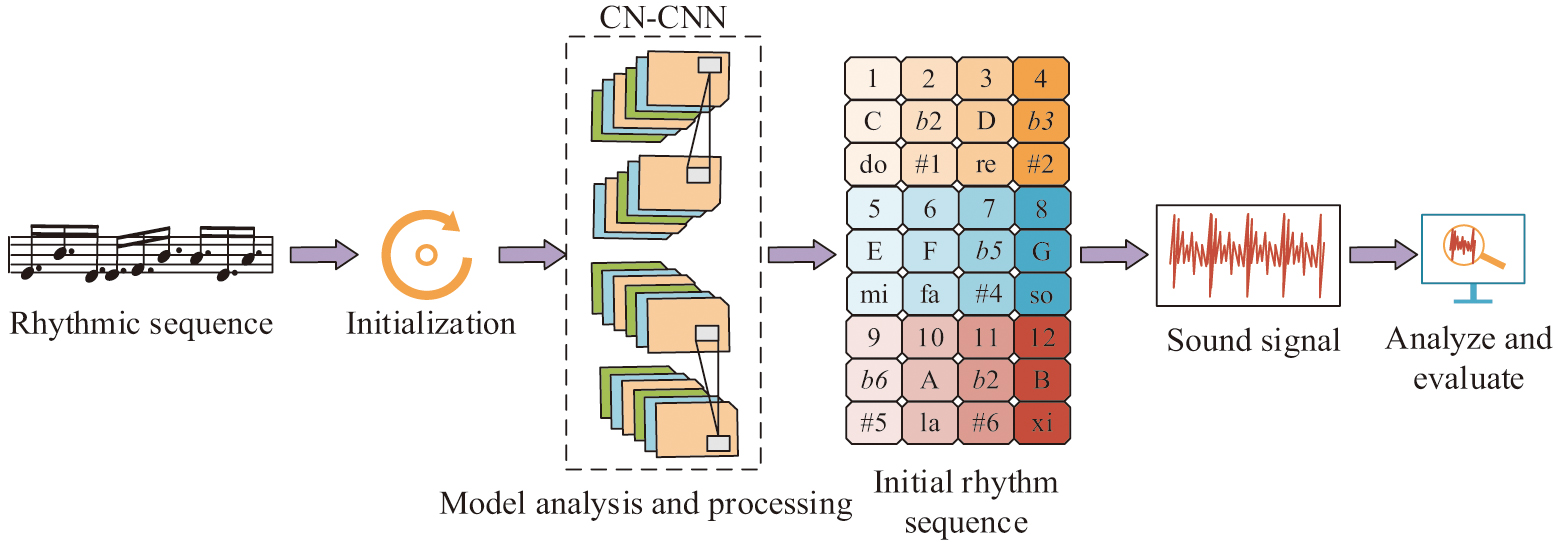 Fig. 3. Evaluation process of ethnic music performance based on music theory rules and CN-CNN (Source from: Author’s own drawing).
Fig. 3. Evaluation process of ethnic music performance based on music theory rules and CN-CNN (Source from: Author’s own drawing).
In Fig. 3, the study utilizes a large number of musical score and audio signal data samples input into the CN-CNN for continuous training, which makes the CN-CNN have the ability to learn from the samples. After the data samples have been convolved, activated, and pooled, the feature matrix is sent to FCL [22]. The FCL integrates and unfolds all the elements in the FM and subsequently performs recognition and comparison operations. Finally, the spectral features, harmonic structure, dynamic range, rhythmic complexity, and stylistic categorization are evaluated to determine the effectiveness of this NM performance.
B.IMPROVED OPTIMIZATION OF NM PERFORMANCE EVALUATION MODEL INCORPORATING AM
The NM performance evaluation model, which only relies on music theory rules and CN-CNN, is difficult to adapt to the dynamic changes of improvised pitch and rhythm and has a weak perception of time sequence. For example, it is insufficient to perceive the coherence of the “scatter-press-pan” timbre alternation of the Chinese Guqin. To address this issue, an AM is introduced to optimize the weight distribution of temporal features. This enables the model to dynamically focus on key decorative areas, suppress irrelevant background noise, and capture long-term dependencies between elastic rhythmic structures. Therefore, an improved LSTM algorithm is introduced to optimize the NM performance evaluation model. The algorithm optimizes the structure of generator and discriminator and introduces the AM to enhance the FE ability of LSTM. To efficiently learn possible relationships between data points, LSTM, a unique type of recurrent neural network, can handle time-series data and capture dynamic properties in picture sequences [23,24]. Combining the AM with LSTM can make up for the shortcomings of LSTM in long sequence modeling, while retaining its time-series processing capability. The LSTM model incorporating the AM is shown in Fig. 4.
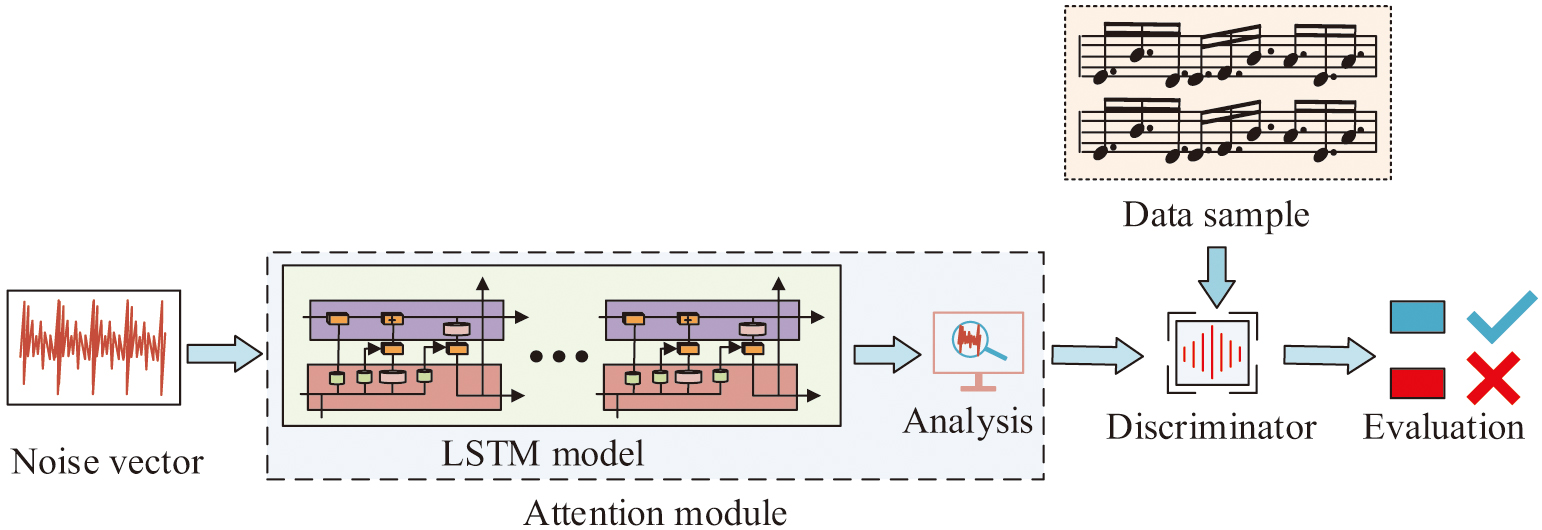 Fig. 4. LSTM model integrating AM (Source from: Author’s own drawing).
Fig. 4. LSTM model integrating AM (Source from: Author’s own drawing).
In Fig. 4, the structure of composite LSTM model mainly consists of generator, LSTM model, and judgment. Combined with the AM, the generator and LSTM model can be constructed as an attention module. The generator receives noise vectors as input and contains multiple LSTM units inside for processing time-series data and generating evaluation data. LSTM achieves effective retention of long-term memory by incorporating hidden states (HSs) and long-term states in the hidden layer. The output data samples of the generator are passed to the discriminator for analysis. The discriminator outputs the judgment result, which represents the evaluation result of the music. The forgetting gate (FG) output in LSTM is shown in equation (8):
In equation (8), is the bias term (BT) of the FG. is the weight matrix of the FG. is the ID of the current moment (CM). is the HS of the previous moment. The candidate states are filtered and created using the activation function , respectively. Among them, is calculated as shown in equation (9):
With the input layer, the previous state is updated to , as shown in equation (10):
In equation (10), is the proportion of new information added through the input gate control. is the percentage of retention of historical information controlled through the FG. The output gate output and final output are calculated as shown in equation (11):
In equation (11), is the updated state of the memory cell at the CM. is the HS at the CM. LSTM first performs FE on the timing data and outputs the HS. After LSTM outputs the HS, the AM assigns different weights to the HS and finally focuses on the key information. The technical synergy between LSTM and AM can be summarized as follows: LSTM processes sequential dependencies via gate mechanisms, thereby maintaining long-term memory of the musical context. Attention re-weights HSs to amplify salient features and suppress less relevant information. The weighted feature vector output feeds into subsequent evaluation layers, enabling the model to make decisions based on the most informative parts of the sequence.
AM is a computational method that simulates the allocation of human cognitive resources. It accomplishes this by dynamically giving certain ID components varying weights. This enables the model to concentrate on important data. Its central concept is “selective attention,” which has extensive use in computer vision, multimodal tasks, and natural language processing. The attention score is calculated as shown in equation (12):
In equation (12), and are trainable weight matrices. is the attention weight (AW) vector. is the previous moment vector. is the BT. The AWs are normalized as shown in equation (13):
In equation (13), is the un-normalized attention score. is the input sequence length. is the attention score from 1 to . The final output of the attention update is shown in equation (14):
In equation (14), means the HS of the LSTM. means the current input vector. is the vector providing global key information. To more closely match the reality in daily life, an audio source separation module is added at the beginning of the evaluation. This module can extract the accompaniment from the audio for subsequent work. The audio preprocessing process is shown in Fig. 5.
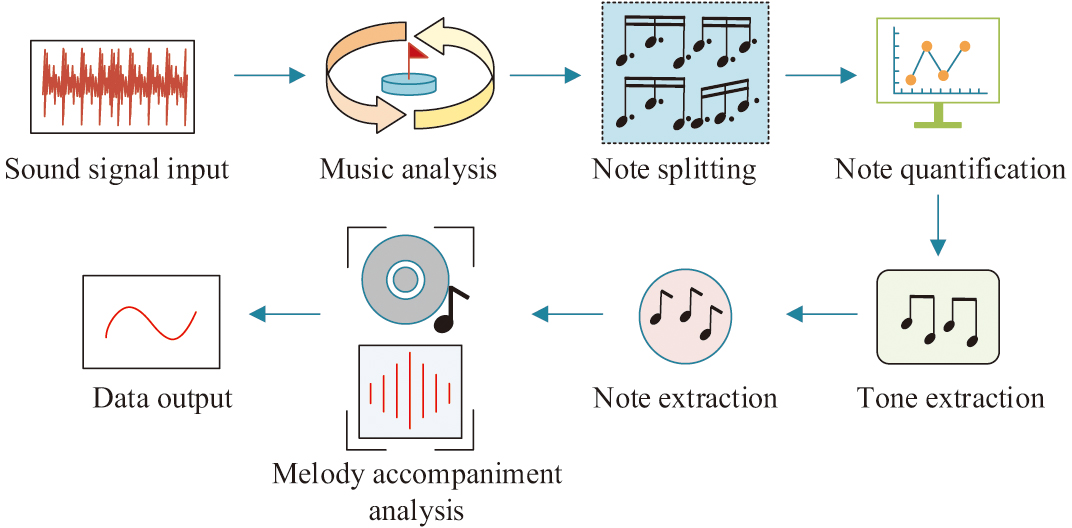 Fig. 5. Audio preprocessing process (Source from: Author’s own drawing).
Fig. 5. Audio preprocessing process (Source from: Author’s own drawing).
In Fig. 5, the complex audio signal is first decomposed into a sequence of note rhythms. It is then decomposed into individual note rhythms by quantization. Finally, smooth and easily parsable audio signals are generated by combining the accompaniment [25]. The evaluation model incorporating the AM, LSTM, music theory rules, and CN-CNN is shown in Fig. 6.
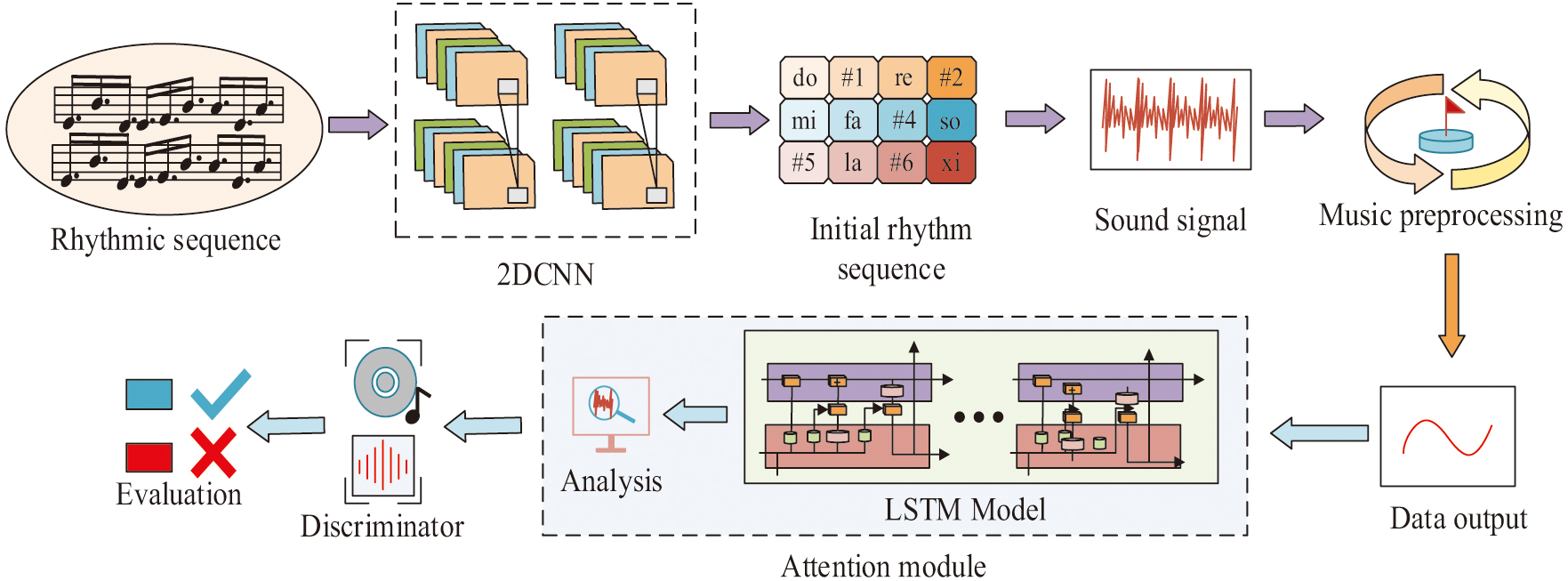 Fig. 6. Evaluation model integrating AM and 2D CN-CNN (Source from: Author’s own drawing).
Fig. 6. Evaluation model integrating AM and 2D CN-CNN (Source from: Author’s own drawing).
In Fig. 6, first, the performed music is subjected to CN-CNN for efficient FE to capture the characteristics and styles of different NM. The CN-CNN model converts audio into complex spectrograms, where the imaginary component explicitly encodes the critical phase relationships necessary for ornamentation analysis. This provides richer input features than real-valued spectrograms for subsequent LSTM processing. Then the music time-series relationship is established by a composite LSTM model incorporating the AM. The long-term feature dependencies in audio are processed to fully understand the bar-to-bar connections of music segments, thus improving the accuracy of NM analysis and evaluation. Finally, by evaluating the intervals between adjacent notes in the music as a whole, the degree of conformity to the compositional rules, the degree of matching between different instruments, the overall pitch degree of the music, and the degree of similarity between the style of the music and the style of the dataset, it is judged to analyze whether the NM performance is accurate and complete and moving.
IV.RESULTS
A.PERFORMANCE TESTING OF A NM PERFORMANCE EVALUATION MODEL INCORPORATING AMS AND MUSIC THEORY RULES
To examine the performance of NM performance evaluation model, the study uses Ubuntu 20.04 system and PyTorch as a framework for deep learning. Combining a high-performance computing server with NVIDIA RTX 3090 GPUs and an experimental platform with Intel Core i9-12900K CPUs, the open-source music software national song dataset is selected for performance testing. The study refers to the NM performance evaluation model built as CN-CNN-LSTM in an attempt to validate its performance. Its training loss curve with LSTM and artificial neural network (ANN) on the open-source music software national song dataset is shown in Fig. 7.
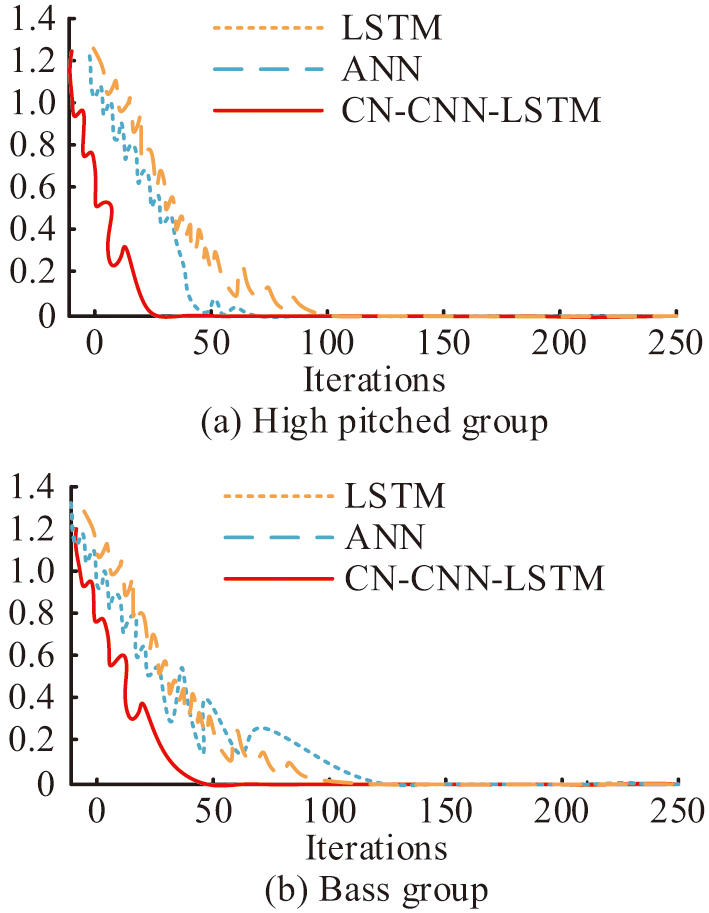 Fig. 7. Method training loss testing (Source from: Author’s own drawing).
Fig. 7. Method training loss testing (Source from: Author’s own drawing).
In Fig. 7(a), the initial loss value of LSTM reaches 1.22 when it is trained in treble music. The loss value decreases to a position close to 0 and remains basically stable when the number of iterations reaches 100. When ANN is trained in treble music, the initial loss value reaches 1.21. The loss value decreases to a position close to 0 and remains basically stable when the number of iterations reaches 60. CN-CNN-LSTM has an initial loss value of 1.21 when trained in treble music. The loss value decreases to a position close to 0 when the iteration reaches 25 and remains largely stable. In Fig. 7(b), the initial loss value reaches 1.35 when the LSTM is trained in bass music. The loss value drops to a position close to 0 and remains largely stable when the iteration reaches 100. The ANN reaches an initial loss value of 1.36 when trained on bass music. The loss value decreases to a position close to 0 and remains essentially stable when the number of iterations reaches 125. When CN-CNN-LSTM is trained on bass music, the initial loss value is 1.22. The loss value decreases to the position close to 0 and basically stays stable when the number of iterations reaches 50 times. It shows that the research method is faster training efficiency and the training process is more stable. The convergence performance of different methods is compared, as shown in Fig. 8.
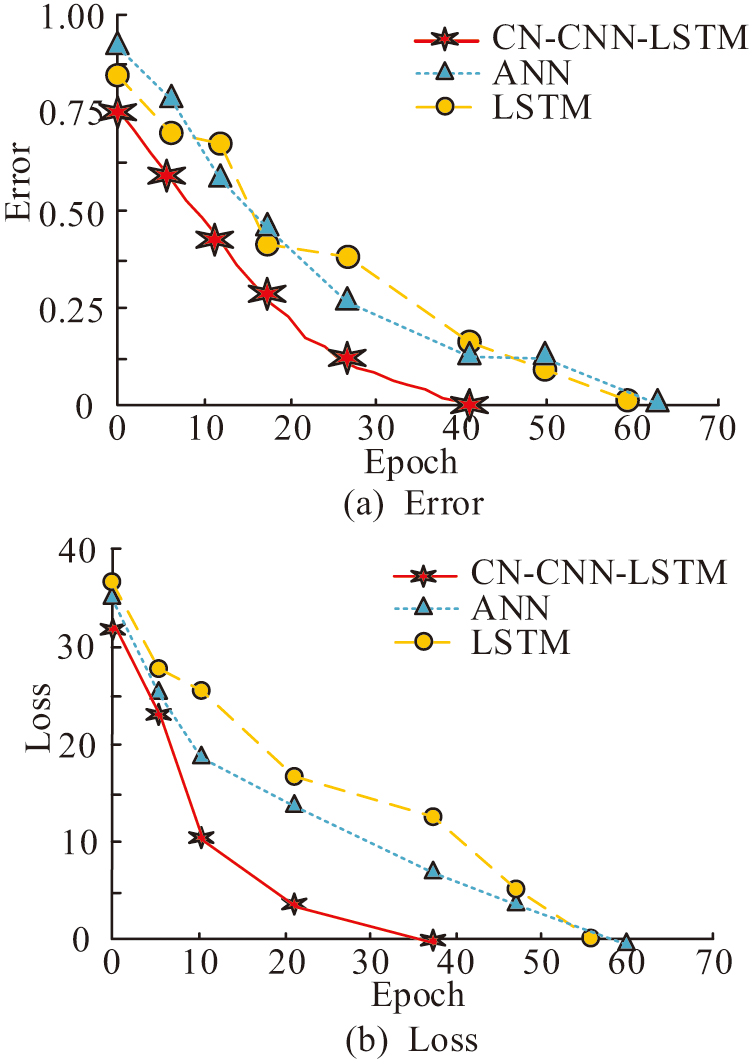 Fig. 8. Convergence performance test (Source from: Author’s own drawing).
Fig. 8. Convergence performance test (Source from: Author’s own drawing).
In Fig. 8, the overall trend of the performance convergence of different methods when performing training is consistent. In Fig. 8(a), the error value of CN-CNN-LSTM decreases rapidly during the error convergence process and has converged to 0 at the 40th iteration. ANN also shows a gradual decreasing trend during the error convergence process and has converged to 0 at the 62nd iteration. LSTM converges to 0 at the 60th iteration during the error convergence process. In Fig. 8(b), during the loss convergence process, the error value of CN-CNN-LSTM at the beginning iteration is 31, which is lower than that of ANN and LSTM. The decreasing trend of the loss value of CN-CNN-LSTM shows a rapid decrease in the early stage. Its later stages gradually slow down the decline until the completion of training. Compared to ANN and LSTM, CN-CNN-LSTM clearly has better convergence performance and high training efficiency. The confidence interval of loss convergence for CN-CNN-LSTM model training is shown in Table I.
Table I. Confidence interval for training loss convergence
| Iterations | Mean loss of high training | 95% confidence interval | Mean loss of low tone training | 95% confidence interval |
|---|---|---|---|---|
| 0 | 1.21 | [1.18, 1.24] | 1.22 | [1.19, 1.25] |
| 25 | 0.12 | [0.10, 0.14] | 0.28 | [0.25, 0.31] |
| 50 | 0.03 | [0.02, 0.04] | 0.05 | [0.04, 0.06] |
| 100 | 0.01 | [0.00, 0.02] | 0.02 | [0.01, 0.03] |
As shown in Table I, during high-frequency training, the initial iteration loss averaged 1.21 with a 95% confidence interval of [1.18, 1.24] and a width of 0.06, indicating stable model initialization. After 25 iterations, the average loss dropped to 0.12, with an interval of [0.10, 0.14] and a width of 0.04. This shows no overlap with the ANN/LSTM, both of which have average losses above 0.30. This demonstrates significantly faster convergence. After 50 iterations, the loss averages 0.03, with an interval of [0.02, 0.04] and a width of 0.02. This indicates increasingly stable training. The low-frequency training exhibits consistent results: an initial iteration loss averages 1.22 with [1.19, 1.25] and 0.06, matching high-frequency training closely. After 50 iterations, the loss averages 0.05 with [0.04, 0.06] and 0.02, far below ANN/LSTM’s contemporaneous values (above 0.15), highlighting strong adaptability to low-frequency features. At 100 iterations, the loss averages 0.02 with [0.01, 0.03], stabilizing near zero without fluctuations. The study compares the change in performance by gradually adding improved modules. The baseline model uses the original CN-CNN. +Music theory rules indicate the addition of music theory rules training. +Composite LSTM module denotes an LSTM module using multiple LSTM units. +AM denotes the introduction of AM. Finally, the full model integrates all the improved modules to evaluate the overall performance improvement. First, the CNN backbone processes raw audio signals and extracts fundamental acoustic features. Then, music theory rules provide domain-specific constraints that guide feature learning and align it with the inherent patterns of ethnic music. A composite LSTM module then models dynamic temporal dependencies in musical signals. Finally, the AM optimizes HS outputs by dynamically focusing on key elements, such as ornaments and glissandos, while capturing long-range dependencies in flexible rhythmic structures. This addresses LSTM’s limitations in capturing dynamic pitch/rhythm variations during improvisation. This sequence ensures effective FE and domain knowledge integration. It also models temporal relationships and ultimately enables AM to prioritize critical information. Table II displays the evaluation findings.
Table II. Results of ablation experiment
| Algorithm | Accuracy (%) | F1 score | Inference time (s) |
|---|---|---|---|
| CN-CNN | 90.83 | 0.90 | 1.98 |
| +music theory rules | 91.17 | 0.89 | 1.84 |
| +Composite LSTM module | 93.28 | 0.90 | 1.85 |
| +AM | 96.53 | 0.91 | 1.68 |
| Full model | 98.01 | 0.92 | 1.65 |
Table I shows the performance of different algorithms in terms of accuracy, F1 score, and reasoning time. The CN-CNN baseline model has an accuracy of 90.83%, an F1 score of 0.90, and an inference time of 1.98 s. After adding the lexicographic rules, the accuracy improves to 91.17%, but the F1 score decreases slightly. After the introduction of the composite LSTM module, the accuracy increases significantly to 93.28%, and the F1 score remains at 0.90. After the addition of the AM, the accuracy increases significantly to 96.53%. The F1 score increases to 0.91, and the inference time is reduced to 1.68 s. Finally, the complete model integrates all the improved modules with 98.01% accuracy, 0.92 F1 score, and 1.65 s inference time. The results show that adding improvement modules step by step can effectively improve the model performance. The complete model performs optimally in terms of accuracy, F1 score, and inference time.
To evaluate the generalization capability and comparative advantages of CN-CNN-LSTM, a supplementary experiment is conducted using the widely used, general music classification benchmark dataset, the GTZAN Genre Collection. This dataset contains 1,000 audio clips that evenly cover 10 music genres, providing a standardized validation benchmark for music classification tasks and performance evaluation. The performance comparison results of different methods are shown in Table III.
Table III. Experimental results of performance comparison
| Algorithm | Accuracy (%) | F1 score |
|---|---|---|
| CN-CNN-LSTM | 95.6 | 0.94 |
| ANN | 89.3 | 0.88 |
| LSTM | 87.1 | 0.85 |
As shown in Table III, the CN-CNN-LSTM algorithm achieves an accuracy rate of 95.6% with an F1 score of 0.94. The ANN model recorded 89.3% accuracy and an F1 score of 0.88, while the LSTM model demonstrates 87.1% accuracy and an F1 score of 0.85. The results indicate that the CN-CNN-LSTM model outperforms the other two algorithms in terms of performance, demonstrating superior accuracy and practical applicability. To validate the model’s advancement further, the state-of-the-art audio spectrum transformer (AST) model is selected from the field of music analysis as a benchmark. The AST model demonstrates accurate classification capabilities across multiple audio categories by processing mel frequency spectra through end-to-end processing. All experiments are conducted on the same GTZAN dataset and hardware environment, with results presented in Table IV.
Table IV. Performance comparison with AST model
| Evaluation metric | CN-CNN-LSTM | AST model |
|---|---|---|
| Accuracy (%) | 95.6 | 94.2 |
| F1 score | 0.94 | 0.93 |
| Inference time (s) | 1.65 | 2.10 |
| Parameters | 28.5 | 86.3 |
As shown in Table IV, the CN-CNN-LSTM achieves an accuracy rate of 95.6%, representing a 1.4% improvement over the AST model’s 94.2%. In terms of F1 score, the proposed model reaches 0.94, slightly higher than the AST model’s 0.93 with a 0.01 improvement. In terms of inference time, the CN-CNN-LSTM is much faster, requiring only 1.65 s–21.4% less time than the AST model’s 2.10 seconds. Additionally, the proposed model’s parameter size is 28.5M, significantly lower than the AST model’s 86.3M (67% reduction). These results demonstrate the proposed model’s excellent performance and efficiency, showcasing its ability to maintain high accuracy while achieving faster inference speeds and reduced parameter size.
B.PRACTICAL APPLICATION OF THE NM PERFORMANCE EVALUATION MODEL
To verify the effectiveness of the NM performance evaluation model designed by the study in practical applications, the study takes Jasmine Flower composed by Liu Tianhua and The Moon Over a Fountain composed by Xian Xinghai from the open-source music software as the research objects. CN-CNN-LSTM, ANN, and LSTM are selected for comparison and 50 cycles are played. The obtained music melody recognition rate is shown in Fig. 9.
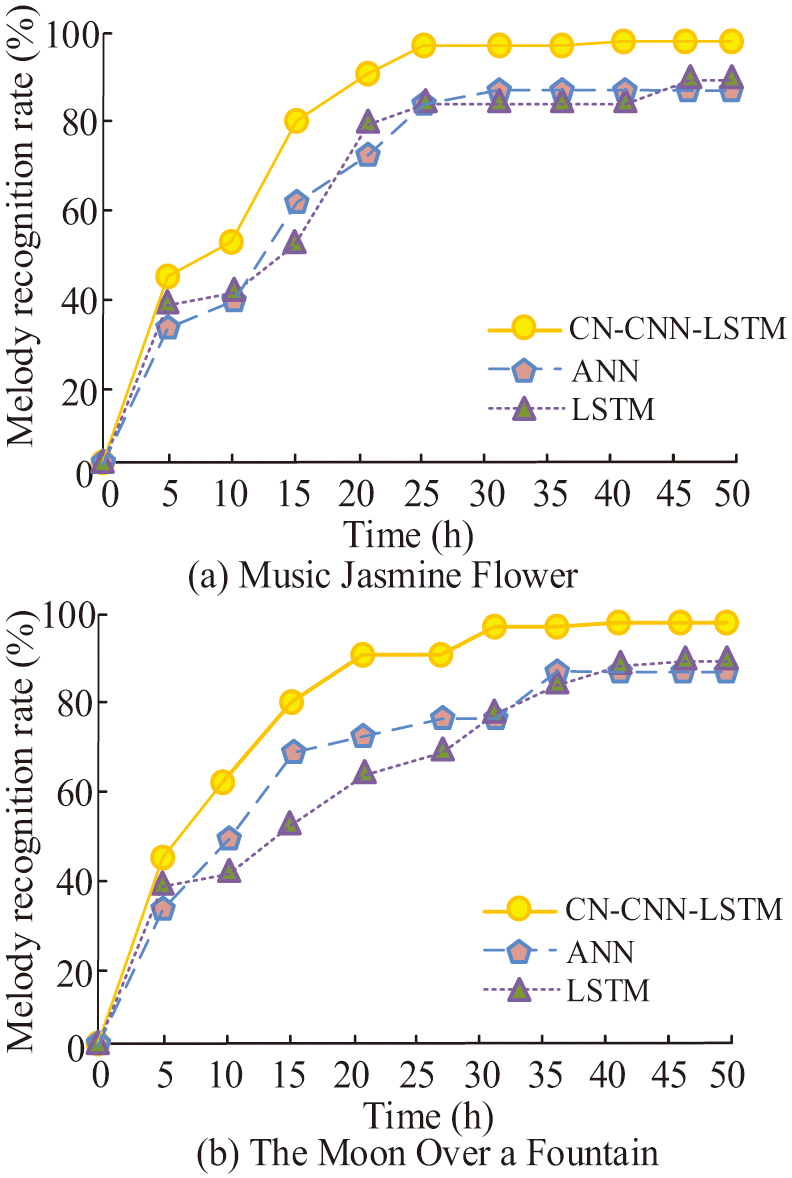 Fig. 9. Music melody recognition rate (Source from: Author’s own drawing).
Fig. 9. Music melody recognition rate (Source from: Author’s own drawing).
Figure 9(a) and (b) show the results of music melody recognition for Jasmine Flower and The Moon Over a Fountain, respectively. In Fig. 9(a), the recognition accuracy (RA) of CN-CNN-LSTM increases gradually with the number of cycles. It reaches the highest RA of 99.87% after the 35th time and stabilizes. Additionally, ANN exhibits a steady rise in RA as the number of cycles increases. After the 30th time, it reaches the highest RA of 89.96% and stabilizes. The RA of LSTM increases gradually as the number of loops increases. However, the RA fluctuates from the 25th to the 40th loop playback. The highest RA of 91.03% is reached after 50 cycles of playback. This result shows that the evaluation model designed in the study performs best in practical applications and has high feasibility and effectiveness. To further validate the feasibility of the evaluation model, the study compares the professional ear and intelligent model for the melodic harmony of the entire songs of Jasmine Flower and The Moon Over a Fountain, as shown in Fig. 10.
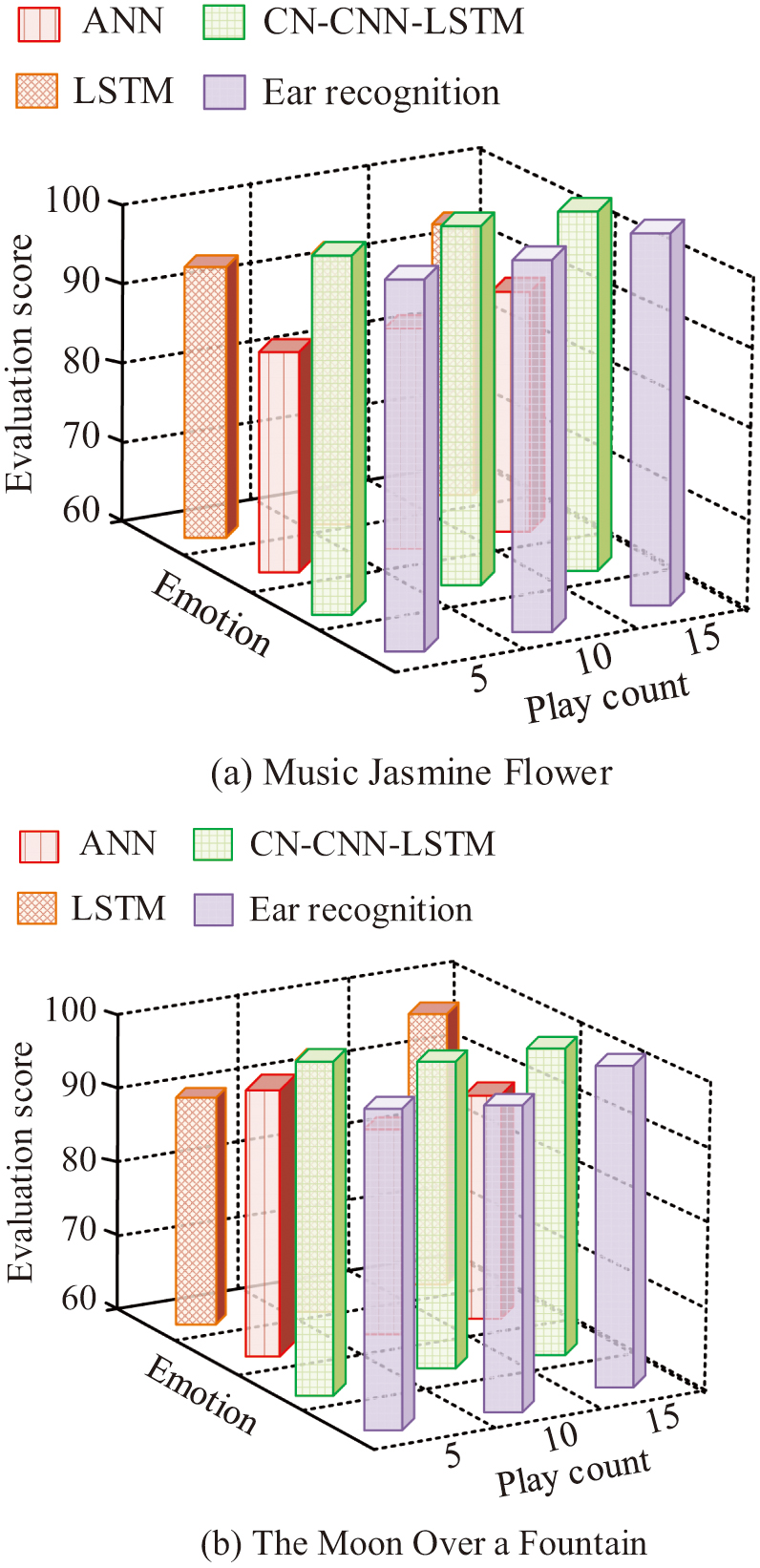 Fig. 10. Comparison of evaluation between professional ear and intelligent models (Source from: Author’s own drawing).
Fig. 10. Comparison of evaluation between professional ear and intelligent models (Source from: Author’s own drawing).
Figure 10 shows a comparison of the results of the professional human ear music performance measure and the intelligent model performance measure for the melodic harmony of the songs Jasmine Flower and The Moon Over a Fountain. In Fig. 10(a), the research design model evaluation effect approximates that of the professionals’ human ear measurements. As the number of times Jasmine Flower is played increases, there are fluctuations in the evaluation scores. It shows that the research design model can have a better effect on recognizing the subtle dissonance in the music as the number of playbacks increases. The fluctuation of ANN and LSTM for the melodic harmony evaluation of Jasmine Flower is large, which indicates that the effect of recognizing the melodic harmony of the music is poor. In Fig. 10(b), the evaluation effect of the research design model is also similar to that of the professional human ear. As the number of times of The Moon Over a Fountain playback increases, there are fluctuations in the evaluation scores. The melodic harmony evaluation of ANN and LSTM for The Moon Over a Fountain fluctuates greatly, indicating that it is less effective in recognizing the melodic harmony of the music. The comparison shows that the melodic harmony of Jasmine Flower is slightly better than that of The Moon Over a Fountain. Disco, classical, jazz, pop, rock, and ethnic music are selected as the categorical labels for the study. JasmineFlower and The Moon Over a Fountain are played in a loop for 100 times. The music genre categorization of the playback results by the research model is made into a confusion matrix, as shown in Fig. 11.
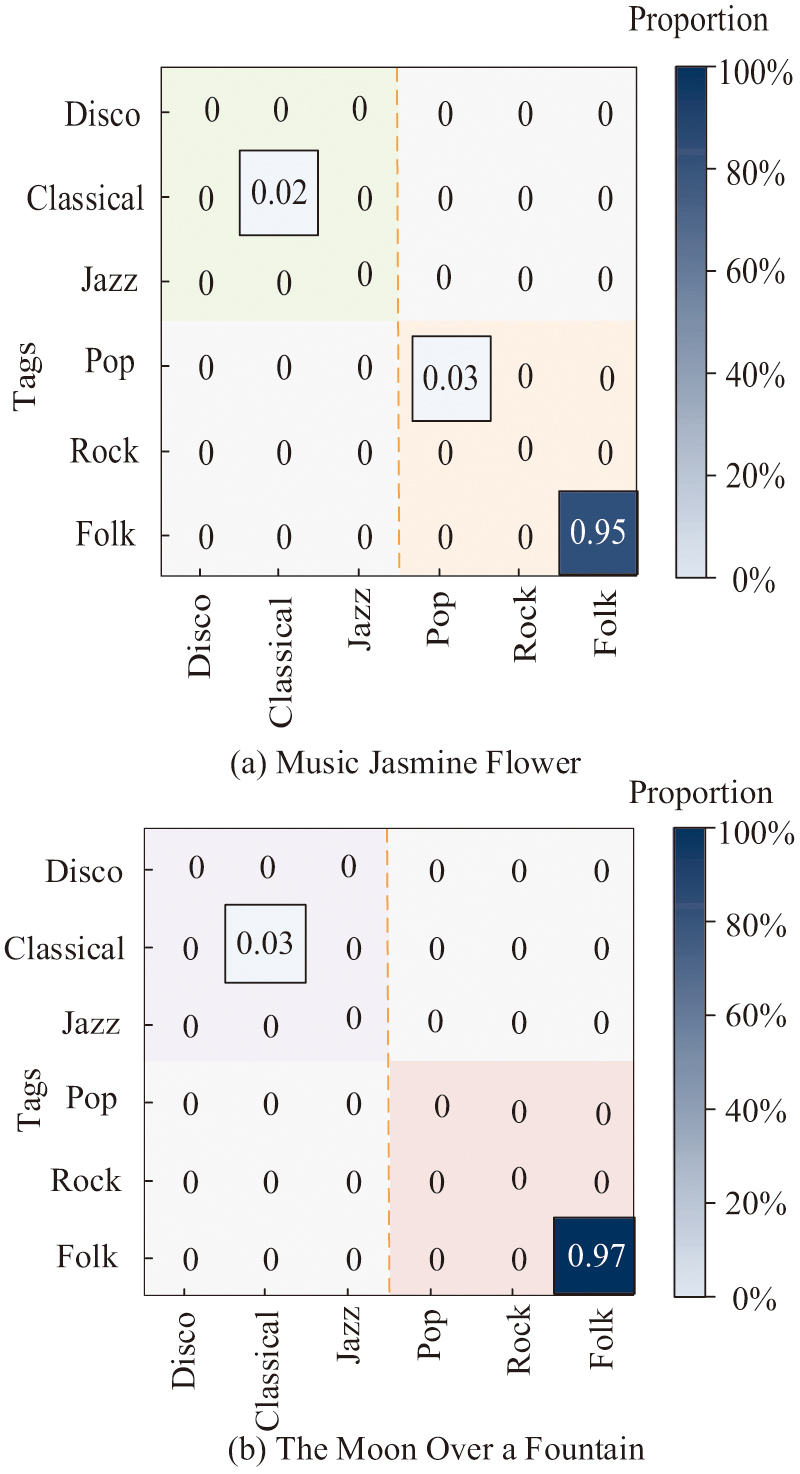 Fig. 11. Ability to classify music genres (Source from: Author’s own drawing).
Fig. 11. Ability to classify music genres (Source from: Author’s own drawing).
In Fig. 11(a), the research model is classified into the correct NM 95 times when classifying Jasmine Flower in the music genre. Only 2 times are classified into classical music genre and 3 times are classified into popular music. In Fig. 11(b), when the research model classifies The Moon Over a Fountain into music genre, 97 times are classified into the correct NM. Only 3 times are classified into classical music genre. It demonstrates that the study model can more precisely extract certain musical features for classification assessment and has a high accuracy rate for classifying musical genres. To further evaluate the applicability of CN-CNN-LSTM to ethnic music styles across different countries, this study selects two distinctive independent datasets for testing. The Indian Classical Music (ICM) segment set contains 50 sitar and tabla performances from various ragas. These performances highlight microtones (shruti), intricate ornaments (gamaka), and cyclical rhythms (tala). The Turkish Maqam Music Segment Set (TMM) features 50 oud and kanun performances based on different maqams. These performances emphasize unique scale structures, including augmented second intervals, as well as improvisational passages (taksim) and flexible rhythms. The accuracy of melody recognition of different methods on these ethnic music test sets is shown in Table V.
Table V. Melody recognition accuracy of different methods on these ethnic music test sets
| Test data set | CN-CNN-LSTM | ANN | LSTM |
|---|---|---|---|
| Chinese folk songs | 98.54 | 90.50 | 91.78 |
| ICM | 85.32 | 72.18 | 68.95 |
| (TMM) | 82.17 | 65.43 | 70.21 |
As shown in Table V, the CN-CNN-LSTM model achieved an accuracy rate of 98.54% on the Chinese folk music dataset. This surpasses the accuracy rates of both the ANN model (90.50%) and the LSTM model (91.78%). On the ICM dataset, it scores 85.32, outperforming ANN (72.18%) and LSTM (68.95%). For the TMM dataset, the model scores 82.17, while ANN (65.43%) and LSTM (70.21%) show lower performance. Overall, the CN-CNN-LSTM outperforms both ANN and LSTM across all datasets, demonstrating superior performance. The reduced accuracy on ICM and TMM datasets compares to its outstanding performance in Chinese folk music stems from differences in musical scales between systems. The unique intervals in ICM and TMM differ significantly from those in the 12-tone equal temperament and the pentatonic scale of Chinese folk music. This makes direct adaptation challenging. Additionally, the rhythm structures differ from the elastic rhythms characteristic of Chinese folk music, limiting the model’s generalization ability. Accuracy of feature matching is also reduced by variations in ornamentation styles, such as glissando and vibrato.
V.CONCLUSION
One of the most important subjects in the fusion of contemporary technology and traditional CH is the digital assessment of NM. The digital evaluation of NM is a key topic in the integration of traditional CH and modern technology. The research constructed an NM performance evaluation model by integrating AM, LSTM, music theory rules, and CN-CNN. This study aimed to address the limitations of traditional evaluation methods, which relied on subjective experience and lacked the ability to capture dynamic features. The goal of this study was to develop a fundamental evaluation model based on musical theory, focusing on key elements such as pitch and rhythm. The CN-CNN model was employed to capture spectral features. To enhance the model’s capacity to adjust and recognize temporal sequences of dynamic shifts in spontaneous pitch and rhythm, the AM was also incorporated into the LSTM algorithm. Experiments indicated that the model significantly outperformed traditional methods in terms of training efficiency and convergence. The model achieved an accuracy of 98.01% on the open-source music software ethnic song dataset with an F1 score of 0.92. In practical applications, the model achieved 99.87% and 97.26% melody recognition for Jasmine Flower and The Moon Over a Fountain, respectively. The melodic harmony evaluation was approximate to the evaluation of the human ear by professionals. An accuracy of 98.01% was achieved in the ablation experiment, and the inference time was reduced to 1.65 s. Misclassification rate was less than 3% in the music genre categorization task. In summary, the model designed by the authors could more accurately recognize the various features of extracted musical scores and could classify and evaluate them. This research provided methodology and tool support for the digital transformation of NM evaluation system. The research outcomes demonstrated significant social relevance and broad application potential. In the field of ME innovation, this model could be integrated into smart teaching systems or mobile applications. It provided learners with performance evaluation feedback and addressed issues of uneven teacher distribution and subjective judgment. This enhanced learning efficiency and promotes standardized musical literacy assessment. For the digital preservation and inheritance of CH, it provided technical support for endangered or niche musical genres. This support came in the form of performance databases that assisted with teaching and evaluation and provided scientific backing for archiving intangible CH. In artistic creation and performance support, the model provided creators and performers with tools for detection and assessment to elevate artistic quality. In terms of public cultural dissemination and promotion, applications and platforms developed based on this model helped audiences better understand and appreciate ethnic music. This drove its popularization and promotes cross-cultural communication. However, the study has certain limitations: The proposed model’s generalization capability for ethnic minority instruments such as the morin khuur (horsehead fiddle), lusheng (reed pipe), and elephant-foot drum remains unverified. This stems from their unique timbres and specialized performance techniques, as well as their insufficient representation in existing training datasets. Future work will expand the dataset by collecting and annotating high-quality, audio-score-paired datasets that cover a broader range of ethnic groups, with a particular focus on minority instruments and performance styles. This will enhance the model’s ability to generalize. Additionally, the goal is to enhance the ability to analyze improvisation by developing temporal modeling techniques for complex, unstructured, dynamic pitch, and rhythm.